Posted in August 2017
Kwadratuur van de cirkel, II
Vorige keer hebben we bekeken wat `Kwadratuur van de Cirkel’ inhoudt in het kader van Euclidische Meetkunde. We hebben ook gezien dat kwadratuur van de cirkel niet mogelijk is met een passer en een latje. Deze keer gaan we bekijken of er andere manieren zijn om die kwadratuur uit te voeren.
Banach en Tarski
In het begin van de twintigste eeuw rees de behoefte om aan steeds meer deelverzamelingen van de getallenlijn, het vlak, en de ruimte respectievelijk een `lengte’, `oppervlakte’ of `volume’ toe te kennen. Om enige afstand tot de concrete meetkunde te bewaren begon men het woord `maat’ te gebruiken en de eerste die een goede definitie van `maat’ formuleerde was Lebesgue, in 1908.
Later is dit door anderen in zijn volle algemeenheid uitgewerkt maar in de bovengenoemde drie gevallen gebruiken we de Lebesgue-maat nog vrijwel zo als Lebesgue hem gedefinieerd heeft.
Voor bekende meetkundige figuren geeft de Lebesgue-maat de reeds bekende waarde maar voor willekeurige verzamelingen gaat het niet altijd even goed.
Een extreem voorbeeld hiervan werd gegeven door de Polen Banach en Tarski. Voortbouwend op werk van Hausdorff lieten ze zien dat men een massieve bol met straal 1 in eindig veel (vijf is genoeg) deelverzamelingen kan verdelen, en dat men daarna die eindig veel stukken in elkaar kan schuiven tot twee massieve bollen van straal 1. Wie met het artikel van Banch en Tarski in de hand nu een wonderbaarlijke vermenigvuldiging van één sinaasappel tot twee sinaasappels wil uitvoeren komt bedrogen uit.
De bollen zijn ideale wiskundige bollen, geen fysieke sinaasappels. En, en daar was het Banach en Tarski om te doen, de stukken waarin ze de bol verdeelden zijn zo lelijk dat er op geen enkele manier een maat aan toe te kennen is. Immers als dat wel mogelijk was dan zou 1+1=1 bewezen zijn.
Terug naar het vlak
De vraag is nu of de wonderbaarlijke vermenigvuldiging in het vlak ook mogelijk is. Dat bleek niet het geval. Als je een verzameling die een maat heeft in eindig veel deelverzamelingen verdeelt en als je die stukken, hoe lelijk ook, tot een andere verzameling in elkaar legt en die nieuwe verzameling heeft een maat dan zijn de maten van beide verzamelingen gelijk.
U voelt hem wellicht al aankomen: Tarski formuleerde een abstracte versie van `de kwadratuur van de cirkel’: kunnen we een cirkelschijf, zeg van oppervlakte 1, in eindig veel verzamelingen verdelen en die stukken weer in elkaar schuiven tot een vierkant van oppervlakte 1?
In 1990 beantwoordde Miklos Laczkovich deze vraag met “Ja”. De gebruikte stukken zijn vrij lelijk, maar ze hoeven alleen verschoven te worden, draaien hoeft niet. De kwadratuur van de cirkel is dus mogelijk, zij het met instrumenten die veel geavanceerder zijn dan een passer en een liniaal.
Iets over het woord `lelijk’. De ontdekkingen door Banach en Tarski en anderen van verzamelingen waaraan geen maat toe te kennen is leidden tot een vakgebied dat Beschrijvende Verzamelingenleer is gaan heten. Hierin worden verzamelingen geklassificeerd naar hun beschrijvingen; het `lelijk’ dat ik een paar keer gebruikt heb kan daar precies gemaakt worden: de verzamelingen van Banach en Tarski, en van Laczkowicz hebben, noodzakelijk, beschrijvingen die vele malen ingewikkelder zijn dan die van verzamelingen die je normaal tegenkomt als lijnen, krommen en andere herkenbare figuren.
En toch …
Aan het eind van 2016 kreeg dit verhaal nog een nieuw slot. Andrew Marks en Spencer Unger bewezen dat de kwadratuur van de cirkel met stukken gedaan kan worden die in de Beschrijvende Verzamelingenleer als zeer mooi zouden worden aangemerkt, de technische term is “van Borel-complexiteit ten hoogste vier”. Voor U naar de winkel holt om deze `heel mooie’ legpuzzel aan te schaffen: hoewel de stukken in het grote geheel van de deelverzamelingen van het vlak redelijk eenvoudig zijn, zijn ze nou ook weer niet zo makkelijk met de hand te maken en vast te pakken.
Daar komt nog bij dat er wel een heel grote doos nodig is om alle stukken in te bewaren: bij een lezing over dit resultaat werd Andrew Marks naar het aantal benodigde stukken gevraagd; zijn antwoord: in de orde van grootte van 10220. Dat is dus een Googol in het kwadraat, maal nog een keer 1020.
Verder lezen
Veel van wat hierboven is beschreven is uitgebreid na te lezen in The Banach-Tarski Paradox (second edition) van Grzegorz Tomkowicz en Stan Wagon uit 2016. Het resultaat van Marks en Unger is daar nog niet te vinden; `Borel circle-squaring’ is nog één van de grote open problemen in het boek. Wie zin heeft kan het artikel te pakken krijgen via arxiv.org.
Kwadratuur van de cirkel, I
`De kwadratuur van de cirkel’ is voor velen een metafoor voor onmogelijkheid en/of futiliteit; in het Engels is `circle-squarer’ een gangbare term voor iemand die iets onmogelijks voor elkaar probeert te krijgen.
Toch is het recentelijk gelukt: gegeven een cirkelschijf een vierkant maken met dezelfde oppervlakte, en wel door die schijf in een eindig aantal stukken te knippen, die op te schuiven en weer aan elkaar te leggen tot dat vierkant.
In de komende blogposts zal ik het verhaal van het probleem en de oplossing vertellen.
Lang geleden zag ik een cartoon waarop een passer te zien was die ‘s avonds op straat tegen een muur (of lantaarnpaal) geleund stond te dromen. In het droomballonnetje was een vierkant te zien. Ik heb die cartoon uitgeknipt en lang bewaard maar hij moet bij een verhuizing verloren zijn gegaan want ik kan hem niet meer vinden.
Nu kan je die cartoon op diverse niveaus waarderen maar voor mij was het een mooie illustratie bij een beroemd onmogelijkheidsbewijs uit de wiskunde: het is niet mogelijk met behulp van passer en liniaal bij een cirkelschijf met straal 1 een vierkant te maken met precies dezelfde oppervlakte als die schijf.
Euclides en Archimedes
Waarom `passer en liniaal’? Dat komt voort uit De Elementen van Euclides. Daarin wordt de Meetkunde opgebouwd vanuit een beperkt aantal uitgangspunten, waaronder de beroemde vijf postulaten. In de bewijzen worden alleen stappen gezet die in die postulaten beschreven zijn:
- Gegeven twee punten trek de lijn door die twee punten.
- Gegeven twee punten trek een cirkel door één van de punten en
met het andere punt als middelpunt.
Euclides formuleerde de eerste stap in twee postulaten: je kunt de twee punten verbinden met een lijnstuk en dat lijnstuk kun je willekeurig verlengen; in redeneringen is het wat makkelijker in één keer die (oneindig lange) lijn getekend te denken. Deze twee stappen kunnen uitgevoerd worden met een liniaal en een passer, vandaar `passer en liniaal’. Overigens heeft die liniaal geen schaalverdeling en daarom spreken sommige boeken, om verwarring te voorkomen, liever van `passer en latje’.
De boeken van De Elementen staan dus vol met constructies die niet meer gebruiken dan de bovengenoemde twee stappen. Onder meer ook constructies van
- een paralellogram met dezelfde oppervlakte als een gegeven driehoek
- een rechthoek met dezelfde oppervlakte als een gegeven rechtlijnige figuur
- een vierkant met dezelfde oppervlakte als een gegeven parallellogram
Het patroon lijkt me duidelijk: bij zoveel mogelijk figuren een vierkant maken met dezelfde oppervlakte. Dat is waar het woord `kwadratuur’ (wat ouder: `quadratuur’) vandaan komt: de oppervlakte van een figuur wordt bepaald geacht als er een vierkant met dezelfde oppervlakte is geconstrueerd.
Wat in De Elementen niet wordt gedaan is de oppervlakte van een cirkelschijf bepalen.
Iemand die wel iets over die oppervlakte kon zeggen was Archimedes. Die bewees dat de oppervlakte van een cirkelschijf met straal r gelijk is aan die van een driehoek met hoogte gelijk aan r en basis gelijk aan de omtrek van de cirkel.
Aangezien de omtrek van de cirkel gelijk is aan 2πr is de oppervlakte van de schijf dus gelijk aan ½×2πr×r en dat is gelijk aan het welbekende πr2. Archimedes had deze notaties nog niet tot zijn beschikking; hij moest het bij de bovengegeven formulering houden. Hij liet ook zien dat, in moderne termen, π tussen de twee rationale getallen 3+10/71 en 3+10/70 ligt.
De bewijzen zijn on-line te vinden via de wikipedia-pagina “Measurement of a Circle”.
Onmogelijkheid
In de negentiende eeuw werd duidelijk waarom die kwadratuur van de cirkel niet in De Elementen gegeven was. Het is namelijk niet mogelijk om dat met alleen passer en latje te doen.
De sleutel tot deze oplossing ligt in het invoeren van coördinaten in het
platte vlak en het kijken wat men algebraïsch kan zeggen over de coördinaten van de punten die construeerbaar zijn vanuit de punten (0,0) en (1,0).
Het blijkt dat we met passer en latje kunnen optellen, aftrekken, vermenigvuldigen, delen en vierkantswortels trekken. En dat is alles.
Op deze manier zijn veel getallen, zoals √2, √(√2), √(2+√(3+√5)), … te construcren, maar lang niet alle getallen. In het bijzonder zijn de getallen π en √π niet met passer en latje te construeren; dat werd door Lindemann in 1882 aangetoond: er is geen enkele manier om uitgaande van het getal 1 en met gebruik van optellen, aftrekken, vermenigvuldigen, delen en vierkantswortels het getal π te maken (en √π dus ook niet).
Volgende keer: als niet met passer en latje kan het op een andere manier wel? Het antwoord is ja, maar de constructie kost heel wat moeite.
Voegwoorden en rekenen
“Taal is geen Wiskunde” schreef @onzetaal als reactie op de vorige post. Inderdaad.
In 2002 stond in het tijdschrift Onze Taal een artikel Alle Aaanwezigen Behalve De Kinderen waarin de werking van voegwoorden gerelateerd werd aan, vooral, optellen en aftrekken.
En, helaas, na een bladzijde voorbeelden gaat het meteen mis:
De betekenis van en is gemakkelijk: het komt overeen met de optelling van twee aantallen. In de wiskundige verzamelingenleer worden aantallen als verzamelingen voorgesteld. De betekenis van `Jan is bakker en visser’ wordt in verzamelingstheoretische termen opgevat als `Jan behoort zowel tot de verzameling bakkers als tot de verzameling vissers.’
De betekenis van en is een stuk ingewikkelder dan optellen en dat laat het geciteerde voorbeeld meteen zien: door te zeggen `Jan is bakker en visser’ verwijst men inderdaad naar de doorsnede van twee verzamelingen: Jan∊Bakkers∩Vissers. Echter `Willen alle bakkers en vissers naar voren komen’ verwijst naar een vereniging: Bakkers∪Vissers. En beide mogelijkheden komen niet overeen met optellen: in het eerste geval laten we niet-vissers weg uit de verzameling bakkers en in het tweede geval is het totale aantal mensen niet noodzakelijk de som van de aantallen bakkers en vissers want onze Jan wordt dan dubbel geteld.
Later wordt aan of ook een rekenkundige kant toegedicht. Die lijkt ook verdacht veel op optellen `Jan is bakker of visser’ verwijst (weer) naar de vereniging van de verzamelingen bakkers en vissers. “Jan behoort tot de verzameling die het resultaat is van de samenvoeging van de bakkers en de vissers. Daar moet je nog de doorsnede van aftrekken, omdat Jan niet tegelijk bakker en visser zou kunnen zijn”. Dat is nou jammer, want de tweede helft van de zin is nogal ongelukkig.
Als het er om gaat de bakkers en vissers bijeen te nemen dan is weglaten van de doorsnede niet nodig: iemand mag best bakker en visser tegelijk zijn. Als het om het totale aantal mensen gaat moet je, als boven, het anatal mensen in de doorsnede aftrekken van de som van de twee aantallen om dubbeltellen te voorkomen.
De tweede helft is ongelukkig omdat hij niets uitlegt: door het `zou kunnen zijn’ laat hij in het midden of Jan twee beroepen uitoefent, of niet en maakt hij het `omdat’ niet waar.
Ik proefde daar een beetje het verschil tussen het exclusieve of en het inclusieve of maar het kwam niet geheel uit de verf. In de omgangstaal is of veelal exclusief: een koekje of een snoepje, maar niet allebei. In de wiskunde gebruiken we het inclusieve of, een beetje uit gemakzucht maar vooral omdat het in de Logica allemaal een stuk mooier werkt.
Met de tweedeling aan het eind kan ik het wel eens zijn: er zijn twee soorten voegwoorden, die in de ene groep gedragen zich als binaire operaties (denk aan +, ∪ ∩, …) en die in de andere als binaire relaties (≤, =, ≥, ⊆, …). En daar was het in het artikel om te doen: proberen een vinger te krijgen achter het verschijnsel dat je sommige voegwoorden `binnen/buiten de haakjes kunt halen’. De zinnen `Jan is bakker en Jan is visser’ en `Jan is bakker en visser’ betekenen hetzelfde en zijn syntactisch correct. Maar van `Ik ga naar buiten omdat ik wil hardlopen’ kun je niet `Ik ga naar buiten omdat wil hardlopen’ maken; `omdat’ is hier een binaire relatie en die kun je ook in de wiskunde niet buiten de haakjes halen: 5+a=5+b is niet hetzelfde als 5=a+b.
Ten slotte
Om het werken met voegwoorden met rekenen te vergelijken ligt voor de hand maar is niet de juiste keuze. Beter is het naar de Boolese Algebra te kijken (spreek uit: Boelse Algebra). Deze is voortgekomen uit het werk An Investigation into the Laws of Thought van de Ierse wiskundige George Boole. Daarin wordt gerekend met ∧ (en) en ∨ (of), volgens regels die een beetje op die van het gewone rekenen lijken maar ook niet meer dan een beetje.
Veel van wat in het artikel wordt besproken kan hiermee geanalyseerd worden. De ervaring leert dat de studenten met dat rekenen niet zoveel moeite hebben. Het kost ze (en niet alleen de studenten) veel meer moeite normale zinnen correct naar dit formalisme te vertalen.
Twee keer zo langzaam; de helft langzamer
“Twee keer zo langzaam” betekent hetzelfde als “de helft langzamer”.
Via een tweet van Enith Vlooswijk vond ik deze deze gedachtenwisseling:
Vraag: ‘2 keer zo langzaam’ hoor je vaak, maar is het correct en/of betekent het iets?
Antwoord: Ja, het is correct. Je zou ook kunnen zeggen: ‘de helft langzamer’; dat betekent hetzelfde.
Dit klinkt als iets waar ik het in een eerdere blogpost ook al eens over heb gehad: het door elkaar halen van `twee keer zo X’ en `de helft X-er’. Dat is vaak een gevolg van het door elkaar halen van Begin- en Eindsituatie. In symbolen: `twee keer zo X’ kun je schrijven als E=2B en `de helft X-er’ kun je schrijven als E=B+E/2. In het eerste geval verdubbel je B, en in het tweede geval tel je de helft van E op bij B om E te krijgen. Voor de gewenste ondubbelzinnigheid: werk altijd vanuit de beginsituatie; de juiste betekenis van `de helft X-er’ is daarmee dus E=B+B/2.
In dit geval is er echter nog iets aan de hand. We kijken eerst even in het woordenboek voor de betekenis van langzaam:
- niet vlug; traag, sloom
- met geringe snelheid
- in de vergrotende trap ter aanduiding van een geringere snelheid in relatieve zin
- zonder snelle overgang of ontwikkeling; geleidelijk
In alle gevallen staat er iets dat eigenlijk niet te kwantificeren is: hoe meet je of iets twee keer zo ‘niet vlug’ is als iets anders? En wat te denken van een twee keer zo geringe snelheid of iets waarvan de snelheid de helft geringer is?
En verder: wanneer is iets langzaam genoeg om deze constructies te kunnen gebruiken? Ik neem aan dat “twee keer zo langzaam als de lichtsnelheid” niet alleen mij de wenkbrauwen doet fronsen?
Misschien wordt daarom het antwoord op de vraag of `2 keer zo langzaam’ iets betekent niet expliciet maar impliciet gegeven: “hetzelfde als `de helft langzamer'”. En ik ben dan geneigd te zeggen: inderdaad, de twee constructies betekenen hetzelfde, namelijk niets.
Nu kan ik wel raden wat de gedachte betekenis van `2 keer zo langzaam’ is: met de halve snelheid. En dan kun je `de helft langzamer’ ook wel duiden: ga langzamer en wel met de helft van de huidige snelheid.
Maar waarom zou je dat dan niet gewoon zeggen?
Toch wat wiskunde
Als we `twee keer zo langzaam’ als `half zo snel’ interpreteren dan komen we uit op de volgende `Behoudswet’: het product van snelheid en langzaamheid is constant. Maar dan betekent `de helft langzamer’ toch echt `twee keer zo snel’.
De ene wortel is de andere niet
Of toch wel …
Er was weer een interessante vraag op de wisfaq. OK, wiskundig gezien niet erg interessant maar wel als inkijk in het hoofd van een/de(?) student.
Een vraag over de cosinus van de helft van arcsin(⅓) leidde tot het volgende: de student had
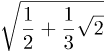
als antwoord gevonden en het `officiéle’ antwoord was
![]()
In de woorden van de student: “En dat is waar ik vastloop.”.
Eigenlijk was de student niet vastgelopen; de oplossing was correct, alleen niet letterlijk gelijk aan het modelantwoord. Voor iemand die met vierkantswortels om kan gaan zou het een koud kunstje moeten zijn het ene antwoord in het andere om te zetten en ik vraag me af waarom dat tot `vastlopen’ zou moeten leiden.
De oefening ging duidelijk om werken met inverse goniofuncties en daar kan de student mee overweg. Hij is kennelijk de routine van de vierkantswortels al weer kwijt. En uit de vervolgvraag blijkt dat hij niet erg stevig in de schoenen staat.
De vraag is wat de vraag is geweest: als er niets meer gevraagd werd dan de cosinus van de helft van arcsin(⅓) dan is het antwoord van de student prima; het modelantwoord is alleen wat mooier gemaakt. Al kun je daar over twisten: aan het antwoord van de student is wat makkelijker te zien hoe groot die cosinus ongeveer is. Als in de vraag stond dat in de wortel alleen gehele getallen mogen staan dan is het modelantwoord het gewenste antwoord maar dan gaat de vraag over meer dan alleen goniofuncties.
Dit alles neemt niet weg dat je van een student zou mogen verwachten dat deze in staat zou moeten zijn de twee wortelvormen aan elkaar gelijk te praten.

Recent Comments