Posts in category Benaderingen
Hogere Machten
Gisteren bekeken we een weergave in woorden van een kansberekening in een column van Maarten Keulemans. Vandaag kijken we even naar die berekening zelf en hoe je snel iets over de 5000ste macht van een breuk als 9999/10000 kunt zeggen.
Even ter herinnering:
En het protest op De Dam? Misschien had men gewoon geluk, berekende epidemioloog Frits Rosendaal (LUMC). ‘De kans om corona te hebben, was op dat moment klein, ongeveer een op tienduizend’, stelt Rosendaal. ‘Dat maakt de kans dat van de 5.000 aanwezigen er een of meer besmettelijk waren, op dat moment 39 procent: 1 min 9.999 gedeeld door 10.000, tot de macht 5.000. Vandaar dat er niks gebeurd is.’
Gisteren hebben we gezien dat de te berekenen kans er zo uit moet zien:

Nu kun je die macht in een rekenmachientje stoppen en als dat goed geprogrammeerd is krijg je ongeveer 0,6065, en dat geeft inderdaad, afgerond, een kans van 39 procent.
Met de juiste formules kun je bijna uit het hoofd een goede onderschatting van de macht maken, en daarmee een overschatting van die kans. De eerste formule is een ongelijkheid:
![]()
Deze ongelijkheid heeft een naam: De Ongelijkheid van Bernoulli, deze geldt voor alle x-en groter dan -1 (en ongelijk aan 0), en alle nauurlijke getallen. Als we 9999/10000 schrijven als 1-1/10000 kunnen we x=-1/10000 nemen, en n=5000, met als resultaat

Zonder al te veel moeite zien we dat de kans in ieder geval kleiner dan ½ was. Voor dit soort schattingen is de Ongelijkheid van Bernoulli een mooi stuk gereedschap om bij de hand te hebben.
Wat scherper
Kan het beter? Ja natuurlijk. Wat extra kennis over over de rij (1-1/n)n vertelt ons dat

en daaruit vinden we dan (met een relatieve fout van niet meer dan 0,0001):

Hierin is e het grondtal van de natuurlijke logaritme.
Onze macht is dan ongeveer de wortel uit 1/e; en daar hebben we een reeks voor die iedere eerstejaars wiskundestudent leert:

En de eerste paar termen geven ons een antwoord dat al heel dicht bij het resultaat van het rekenmachientje ligt.
Binomium
Voor degenen die het Binomium van Newton kennen (en beheersen): schrijf de eerste paar termen van de uitgewerkte macht maar eens op en vergelijk met de som voor 1/√e.
Dikke en dunne verzamelingen
Gisteren hebben we gekeken naar de wiskunde achter het vermoeden van Duffin en Schaeffer. Wat daar niet goed uit de verf kwam waren de noties van `dikke’ en `dunne’ verzamelingen. Daar doen we vandaag wat aan.
Zoals gisteren en in de krant beschreven gaat het vermoeden van Duffin en Schaeffer over benaderingen van irrationale getallen met behulp van breuken. De situatie is als volgt: neem een rij (xn)n van positieve reële getallen en noem een irrationaal getal α goed benaderbaar, volgens de gegeven rij, als er oneindig veel natuurlijke getallen n bestaan met voor elk van die n een breuk t/n met noemer n bestaat zó dat |α-t/n|<xn.
De vraag is dan natuurlijk of er irrationale getallen zijn die goed te benaderen zijn. Gisteren hebben we gezien dat als x_n=n-2 alle irrationale getallen goed te benaderen zijn. Met een beroep op de gisteren ook genoemde Categoriestelling van Baire kunnen we laten zien dat er altijd heel veel goed benaderbare irrationale getallen zijn. Net als gisteren bekijken we voor elke n de intervallen (0,xn), (1/n-xn,1/n+xn) … (1-1/n-xn,1-1/n+xn), (1-xn,1). Hun vereniging noemen we An.
Neem een (klein) interval (a,b) binnen (0,1); dan geldt voor elke n met 1/n<b-a dat An en (a,b) een niet-lege doorsnede hebben (bedenk maar eens waarom dat zo is). Dit betekent dat indien we voor elke n de verzamelingen An, An+1, An+2, … verenigen tot de verzameling On we een verzameling krijgen die met elk intervalletje getallen gemeen heeft. De stelling van Baire garandeert nu dat er heel veel getallen bestaan die tot alle On behoren, en dus tot oneindig veel van de An (denk daar ook maar eens goed over na). Al die getallen zijn dus goed benaderbaar, volgens de gegeven rij.
In topologische zin is het complement van die verzameling goed benaderbare getallen nogal dunnetjes, in het Engels: meagre; de verzameling goed benaderbare getallen is dus, topologisch gesproken, bijna het hele interval (0,1) een dikke verzameling dus.
Het vermoeden van Duffin en Schaeffer ging over een andere notie van dik en dun. Laten we de verzameling goed benaderbare getallen, bij de rij (xn)n, even noteren met G(x). De nu bewezen stelling kijkt naar de (totale) lengte van de intervalletjes die we hierboven gebruikt hebben. Voor elke n is de totale lengte van An gelijk aan 2×n×xn. Als de xn-en te klein zijn zal de verzameling G(x) volgens deze notie als dun aangemerkt worden in die zin dat de kans dat een irrationaal getal goed benaderbaar is gelijk is aan 0.
De stelling van Dimitris Koukoulopoulos en James Maynard spreekt uit dat voor elke rij (xn)n de verzameling G(x) hetzij kans gelijk aan 1 heeft om geraakt te worden, hetzij kans 0; een tussenweg is er niet. Daarnaast geeft de stelling precies aan voor welke rijen kans 1 geldt en voor welke rijen kans 0.
We hebben hier dus twee soorten `dik en dun’ gezien: topologisch en kanstheoretisch. Beide noties worden in de Analyse toegepast om te laten zien dat bepaalde objecten bestaan: als je laat zien dat de verzameling van die dingen `dik’ is is die zeker niet leeg.
Voor topologen is de verzameling goed benaderbare getallen altijd `dik’; voor kansrekenaars is hij soms `dik’ en soms `dun’. Dit klinkt paradoxaal, maar is het niet: het is `gewoon’ een gevolg van de definities. En het illusteert wel treffend de titel van de column die gisteren is aangehaald: ‘De kans is nul’ is niet hetzelfde als ‘dat gaat niet gebeuren’.
Het vermoeden van Duffin en Schaeffer
Recentelijk is het Duffin-Schaeffer-vermoeden bewezen. U kunt de preprint hier lezen. In de krant is er ook aandacht aan besteed. Ik wil hier iets meer over de wiskunde achter dit vermoeden vertellen.
Het vermoeden, nu dus een stelling, zegt iets over het benaderen van irrationale getallen met behulp van rationale getallen. De vraag is in het algemeen hoe efficiëent dergelijke benaderingen kunnen zijn.
Nu zullen de meningen over wat efficiënt is uiteen lopen maar de benaderingen die we in de praktijk gebruiken, namelijk afgekapte decimale ontwikkelingen, zijn het niet echt. Als die afgekapte ontwikkelingen als breuk schrijft is die breuk vrijwel nooit te vereenvoudigen: de benadering 3.14159265358979323846264338327 van π levert een onvereenvoudigbare breuk met een grote teller en een grote noemer.
Een goede benadering is er een waar de nauwkeurigheid groot is, vergeleken met de grootte van teller en noemer. Zo kun je 22/7 een goede benadering van π noemen omdat het verschil 22/7-π kleiner is dan 1/49. Het criterium dat we hier hanteren is: p/q is een goede benadering van α als |α-p/q| kleiner is dan 1/q2. Overigens is 19/6 ook een goede benadering: 19/6-π is kleiner dan 1/36.
Een beetje spelen met een rekenmachientje laat zien dat er geen goede benaderingen van π zijn met noemers 8 of 9.
Het vermoeden van Duffin en Schaeffer, nu dus de stelling van Dimitris Koukoulopoulos en James Maynard, gaat overigens niet over individuele irrationale getallen als π of √2. Het bekijkt de zaak van de andere kant en doet uitspraken over hoeveel irrationale getallen veel goede benaderingen hebben.
Je kunt bijvoorbeeld een vaste noemer n nemen en kijken welke getallen een goede benadering met noemer n hebben. Hierbij beperken we ons tot het interval (0,1); getallen in andere intervallen krijgen we door over een geheel getal op te schuiven.
Nu is meteen duidelijk welke getallen een goede benadering met noemer n hebben: die liggen in de intervalletjes van de vorm (k/n-1/n2,k/n+1/n2), met k=1,…,n-1, en in (0,1/n2) en (1-1/n2,1).
De totale lengte van die intervallen is gelijk aan 2/n (reken maar na).
Hiermee kun je voorspellingen doen: omdat 2/10+2/11+2/12+2/13+2/14+2/15 kleiner is dan 1 zijn er getallen zonder goede benadering met noemers 10 tot en met 15.
Noem de vereniging van de intervalletjes hierboven even An. Met behulp van de Categoriestelling van Baire kun je bewijzen dat er een relatief `dikke’ deelverzameling van het interval (0,1) is waarvan elk element tot oneindig veel van de An behoort en dus oneindig veel goede benaderingen heeft.
Dit nu is de aard van de stelling van Dimitris Koukoulopoulos en James Maynard: deze geeft, bij bepaalde definities van `goede benadering’, voorwaarden onder welke de verzameling getallen met oneindig veel goede benaderingen heel `dik’ is of juist heel `dun’, waarbij `dik’ en `dun’ ondubbelzinnige definities hebben. Daarnaast geeft de stelling ook een dichotomie: `dik’ en `dun’ zijn de enige mogelijkheden. Het is nooit zo dat ongeveer de helft van de getallen oneindig veel goede benaderingen hebben; de kans is altijd gelijk aan nul (wat niet betekent dat er geen getallen zonder oneindig veel goede benaderingen zijn) of gelijk aan één.
In het krantenartikel wordt nog het volgende voorbeeld van `mooie’ benaderingen gegeven: als hierboven moet |α-p/q| kleiner zijn dan 1/q2, maar q moet zelf ook een kwadraat zijn. In dat geval is de kans op oneindig veel mooie benaderingen gelijk aan nul, maar de bovengenoemde stelling van Baire garandeert toch dat er heel veel irrationale getallen met oneindig veel goede benaderingen zijn.
Ten slotte: voor de definitie van `goed’ waar dit stuk mee begon geldt dat <emelk irrationaal getal oneindig veel goede benaderingen heeft. Dat bewijs je niet met de methoden die hier beschreven zijn, daar moet je wat dieper de getaltheorie in duiken. Zie hiervoor de Wikipediapagina’s over Benaderingsstelling van Dirichlet en over Kettingbreuken.
En tau rund jorden, II
Dette er andre delen av en oversettelse av en artikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger). Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen? Kan vi uttrykke høyden i lengden vi spleiset inn?
I går vi så at når vi tar en tau som er en meter langre enn jordens omtrekk og drar tauen strammt ved Nordpolen så skal det høyeste punktet være på 121 meter og lit mer. I dag skal vi lage en enkel formel med radiusen og ekstra lengden i som gir en god approksimasjon av høyden.
En effektiv approksimasjon
Her er tegningen fra i går igjen
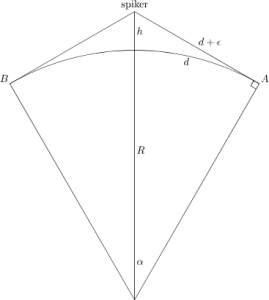
Fra Pythagoras sin læresetning lærte vi at
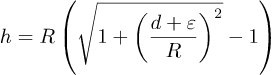
Fra bildet ser vi også at
![]()
Dette kan kombineres til denne ligningen
![]()
Nå har vi et uttrykk for h som bruker R og α men vi trenger et som bruker ε. Dette må gjøres implisitt fordi α er en løsning av
![]()
og der er ingen `pen’ (eller stygg) formel for løsningene.
Som vi så i går er vinkelen α veldi liten (0.006176 radianer). Nå er det slik at α+α3/3 er en veldi bra approksimasjon av tanα. Hvis vi setter dette uttrykket i ligningen så får vi
![]()
Også tanα er veldi liten.
Og for x nær 0 har vi √(1+x)≈1+½x; nå kan vi forenkle formelen for h til en approksimasjon
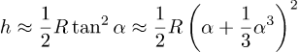
Neste steg er å skrive ut kvadraten
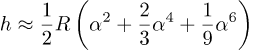
Når vi setter i tallene så får vi Rα2=242.8 m, Rα4=0.009 m og Rα6=3.5×10-7 m. Vi derfor kan trygt kaste fjerde og sjette potensene og så får vi denne approksimasjonen for h:
![]()
Lit lengre siden fant vi at
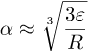
Vi setter det inn i approksimasjonen og får
![]()
Nå bruker vi verdien av R og får til slutt
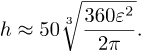
Det flotte med denne formelen er at den gir nesten samme svaret som i går: setter vi inn ε=0.5 så får vi h≈121.4 m igjen.
Oppgav
Sett inn ε=0.005 in formelen vår. Hvor mye forskjeller resultatet fra verdien av h som vi fikk i går?
Exercise
Undersøk hvor bra approksimasjonen √(1+x)≈1+½x er. For eksempel, sammenlign (1+½x)2 med 1+x; for hvilken x er forskjellen liten nok til å bli kastet? Er du enig i hvordan approksimasjonen brukes her?
Bemerkning
Vi kan isolere ε i formelen:

dette gir viktig kvalitativ informasjon: h er omtrent lik en konstant ganger ε2/3.
Hvis du er kjent med Taylorpolynomer kann det være gøy å finne ut hvor stor feilen er (hvilken potens av ε) i denne approksimasjonen.
Rare vragen IV: vier chemici op zoek naar een optimum (deel 2)
We vervolgen de reis die begon bij deze vraag op www.wisfaq.nl. Inmiddels hebben de studenten aangegeven een docent op te zoeken. Ik had toch nog een paar gedachten over het probleem.
Vierde reactie
Mijn vermoeden was dat de zaak als volgt in elkaar stak: er was een drie-dimensionaal array geïndiceerd met [x1,x2,x3] en bij elk drietal een (meet)waarde y1. Eerst werd bij vaste x2 en x3 door middel van kleinste kwadraten een best passend vierdegraadspolynoom voor y1 in termen van x1 bepaald. De term `kleinste kwadraten’ heb ik er zelf bijgehaald; de studenten hadden het over de `lijnschatter’ van Excel en het klinkt alsof dat een zwarte doos is voor het uitvoeren van lineaire regressie (Google gaf weinig info).
De volgende stap leek dit bij vaste x3 in de in de richting van x2 te herhalen, waarbij coëfficiënten als functie van x2 werden geschreven. En ten slotte werd ook x3 bij het functievoorschrift betrokken.
Ik beschreef dit in mijn reactie en gaf aan dat met kleinste kwadraten ook in één keer een polynoom in drie variabelen voor y1 als functie van x1, x2 en x3 te maken is.
Vijfde reactie
De reactie bevestigde mijn vermoeden maar liet ook zien dat de studenten eigenlijk niet wisten wat ze aan het doen waren: geen reactie op `kleinste kwadraten’.
Voor iemand die weet hoe deze methode werkt is het geen grote stap van één naar meer variabelen. Vermoedelijk is dat niet iets dat makkelijk met de `lijnschatter’ van Excel te doen is.
Zesde reactie
In het (voorlopig) laatste deel van dit verhaal wordt duidelijk dat de studenten toch wel wat wiskunde, in het bijzonder Lineaire Algebra, bij zouden moeten leren.
Conclusie?
Ik werd in het begin op het verkeerde been gezet door de manier waarop de vraag in eerste instantie werd gesteld: het leek of de studenten wisten wat ze deden, uit hun verhaal haalde ik dat ze wisten wat kleinste kwadraten waren maar dat ze niet goed wisten wat met meer dan één variabele aan te vangen. Herhaald toepassen is geen slecht idee maar de beschrijving was zo onduidelijk dat het lang duurde voor ik doorhad dat ze slechts op de zwarte doos die Excel is steunden.
En dan waren we nog niet eens aan de gevraagde optima toegekomen. Zelfs als er uiteindelijk een polynoom voor y1 in termen van x1, x2 en x3 gemaakt is dan nog is het optimum van d[6(1-y1)/x3]/dx1 (en d[6(1-y1)/x3]/dx2 en d[6(1-y1)/x3]/dx3) niet zo snel gevonden, in ieder geval niet in formulevorm zoals de studenten hoopten want het nul stellen van de partiële afgeleiden leidt niet tot prettige vergelijkingen.
Mijn eigen conclusie: niet alle vraagstellers weten/kunnen wat hun vraag lijkt te suggereren.
Rare vragen IV: vier chemici op zoek naar een optimum (deel 1)
Op 1 september 2017 verscheen er een vraag op de wisfaq.nl die aanleiding bleek tot een hele serie reacties met vragen en wedervragen. Ik weet eigenlijk niet wie er meer geleerd heeft: de vraagstellers of ikzelf.
De vraag
Ik raad de lezer aan de vraag eerst zelf te lezen; dan zal duidelijk worden dat deze niet makkelijk is samen te vatten. Het probleem was namelijk, voor mij, dat de vraagstellers geen onderscheid leken te kunnen (of willen?) maken tussen enkel- en meervoud. Dat begon al met de zin “We beschikken over een uitgebreide reeksen.” En verder leek “y1 als functie van x1” eerst op één functie te slaan maar later op meer dan één: x2 ging voor variatie zorgen, en later kwam er ook nog een x3 in het spel. Enfin, mijn reactie laat zien dat men wel iets duidelijker kon zijn.
Eerste reactie
De eerste reactie probeerde een en ander te verduidelijken maar dat lukte niet echt; ik kon geen vinger achter de relaties tussen de, inmiddels zes, variabelen x1, x2, x3, y1, y2 en y3 krijgen. Ik maakte een minimaal datasetje dat, dacht ik, aan de eisen voldeed en vroeg hoe ze y1 als functie van x1 dachten te schrijven.
Tweede reactie
Geen reactie op de dataset maar nog meer uitleg van de werkwijze, zonder dat nu echt duidelijk wordt hoe y1 als functie van x1 te schrijven is. Nogmaals gevraagd hoe dat zou werken met het datasetje.
Derde reactie
Andermaal geen reactie op de dataset, wel de medeling “wij zijn studenten chemie, geen wiskunde”. De bijgeleverde uitleg van de vorm van de vier-dimensionale tabel bracht niet echt meer duidelijkheid. De mededeling aan het eind was van alles het meest zorgwekkend: studenten op een hogeschool zoeken wiskunde-experts op de wisfaq, niet op het eigen instituut. Ik heb ze aangeraden toch eens iemand op de eigen school aan te spreken.
Vierde reactie
Na een zo mogelijk nog cryptischere beschrijving van hun werkwijze komt de mededeling dat ze wel naar een docent zullen stappen.
Morgen meer.
Tijdrijden in Bergen
Deze week worden in Bergen, Noorwegen, de wereldkampioenschappen wielrennen op de weg gehouden, met vandaag, 20-09-2017, het tijdrijden voor de heren. Het parcours is interessant: een relatief vlakke rit met aan het eind een klim naar de top van Fløyen, een plek met een mooi uitzicht over de stad en de haven.
In de lokale krant Bergens Tidende staat het profiel van de rit getekent, met de laatste drie kilometer nog een keer apart in het onderstaande plaatje.
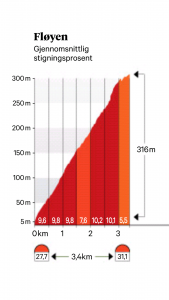
Dat ziet er dramatisch uit, tot je even naar de eenheden kijkt: horizontaal zijn dat kilometers, verticaal gaat het in stappen van 50 meter omhoog. En dat geeft, op zijn zachtst gezegd, een vertekend beeld. Ik heb, bij benadering, het echte profiel even geschetst.
![]()
Dat lijkt niet erg steil en zo van opzij ziet het er niet moeilijk uit; echter, bij wegen met een dergelijke helling staat vaak een waarschuwingsbord voor, juist, een steile helling. Een hellingspercentage van ongeveer 10 % betekent dat er constant met een kracht gelijk aan ongeveer 10 % van het gewicht van jezelf en je fiets tegen je aan geduwd wordt. Naar beneden is dat plezierig al zul je snel zien dat je in je remmen moet knijpen om niet te snel te gaan. Naar boven maak die kracht het fietsen al een stuk moeilijker.
Voor wie wil rekenen: denk maar eens aan de formule F=m×a (kracht is massa maal versnelling). De kracht recht naar beneden is gelijk aan g×m (hier is g de zwaartekrachtsversnelling, daar mochten we op school wel de waarde 10 voor nemen). Hiervan werkt 10 % langs de weg, dus onze F is gelijk aan g×m/10, van school mocht ik daar dus m van maken. Conclusie: de versnelling die we ondervinden als we freewheelend naar beneden gaan is 1 m/s2. Per seconde gaan we dus een meter per seconde sneller. Bereken zelf maar eens hoe snel je dat te link vindt worden.
Snel ordenen
Nog een vraag van de wisfaq:
Ik ben me aan het voorbereiden voor toelatingsexamen aan de Koninklijke Militaire School en kwam volgende vraag tegen:
Sorteer a, b en c volgens stijgende waarden: a=√23; b=1199/250; c=959/200
Nu vroeg ik me af hoe ik dit efficiënt kan doen en zonder rekenmachine weliswaar!
Hoe doe je zoiets snel? Als ik veel haast heb bereken ik misschien 1199×200 en 959×250. Er geldt namelijk dat b>c precies als 1199×200>959×250 (via kruislings vermenigvuldigen) en daarnaast zou ik snel de kwadraten van b en c bepalen en met 23 vergelijken.
Die vermenigvuldigingen kosten wel wat tijd want de getallen zijn een beetje groot. Daarom kan het handig zijn iets beter naar de getallen te kijken. Dan blijkt dat die twee breuken hetzelfde gehele deel hebben, namelijk 4, en dat wat overblijft snel te vergelijken is:
1199/250=4+199/250=4+796/1000 en 959=4+159/200=4+795/1000 en nu zijn b en c in ieder geval heel eenvoudig te vergelijken: b>c.
En hoe zit het met √23? Het kwadrateren van b en c kan iets sneller als je het indirect doet: schijf b=5-204/1000 en c=5-205/1000, en gebruik de bekende formule (x-y)2=x2-2xy+y2. Dan blijkt dat
- b2=23-4/100+(204/1000)2, en
- c2=23-5/100+(205/1000)2.
Nu is (204/1000)2 net iets meer dan (2/10)2=4/100, dus b2 is net iets groter dan 23.
Ook (205/1000)2 is iets meer dan 4/100 maar niet te veel: het is kleiner dan het makkelijkere kwadraat (21/100)2=4,41/100 en dat is weer kleiner dan 5/100, dus c2 is kleiner dan 23.
Conclusie: 959/200<√23<1199/250.
Ik vind dit een aardige opgave omdat met weinig niet al te moeilijke vermenigvuldigingen en delingen drie getallen die heel dicht bij elkaar liggen toch mooi onderscheiden kunnen worden.
KP checkt: Ruim de helft meer …
Op twitter werd er al schande van gesproken: vandaag (2017-06-27) in NRC: … iets meer dan 100 Euro, ruim de helft meer dan de 46,45 Euro … (NRC Checkt).
Is 100 echt ruim de helft meer dan 46,45? Nee, natuurlijk niet. `Meer’ en `minder’ doe je altijd ten opzichte van het beginbedrag, en dat is hier 46,45. De helft van dat bedrag is 23,225 en `ruim de helft’ is wat subjectief, maar hoger dan 30 zou ik toch niet gaan. Ruim de helft meer dan 46.45 is dus niet meer dan ongeveer 76 a 77.
Ik beoordeel deze bewering van NRC Checkt als ONWAAR.
Overigens zie je zo waar dat `ruim de helft’ vandaan komt: 100 is inderdaad ruim de helft van 100 zelf (namelijk 53,55) meer dan 46.45. Hoe begrijpelijk ook, het is op zijn zachtst gezegd niet handig: het wordt snel onwerkbaar als je bij iedere transactie moet vragen of het om een deel van het begin- of van het eindbedrag gaat.
Om verwarring te voorkomen rekent men altijd vanuit het beginbedrag. In het stuk van NRC Checkt zou dat nog spectaculairder klinken: … iets meer dan 100 Euro, ruim het dubbele van de 46,45 Euro …

On-line is het al verbeterd, maar papier is geduldig.
Raaklijnen aan de aarde, II
Vandaag los ik een belofte van gisteren in door te laten zien wat de twee vragen van gisteren gemeen hebben, naast het feit dat beide iets met raaklijnen aan het aardoppervlak te maken hebben.
De vraag naar de hoogte van het eindpunt van de rechte weg van John Körmeling leidde tot de formule

Gisteren stond er 3000 op de plaats van de w maar ik heb die w ingevoerd om de structuur van de formule duidelijk te maken. Ter herinnering R is de straal van de aarde.
De vraag over de wandeling van Zandvoort naar Scheveningen leidde tot
![]()
Hierin is α de hoek, in radialen, tussen de positievectoren (vanuit het middelpunt van de aarde) van Zandvoort en Scheveningen. Er geldt dat α=d/R, waar d de gelopen afstand is (gemeten langs het aardoppervlak natuurlijk).
Die formules lijken niet echt op elkaar maar voor een wiskundige met haast en zonder rekenmachine op zak zijn ze eigenlijk gelijk. Het punt is namelijk dat w/R en α erg klein zijn (en (w/R)2 nog kleiner). Voor kleine x gelden de volgende benaderingen.
![]()
en
![]()
Voor wie wat weet over Taylorpolynomen komen deze benaderingen niet als een verrassing. Voor wie die polynomen niet kent: de benadering van √(1+x) krijg je door je te realiseren dat (1+x/2)2=1+x+x2/4. Als x heel klein is is x2 nog veel kleiner en dat maakt de benadering goed genoeg. Voor de benadering van cos(x) zonder gebruik van de stelling van Taylor verwijs ik naar dit artikel in Pythagoras; daar wordt ook bekeken hoe goed die benadering eigenlijk is.
Als we de benaderingen gebruiken krijgen we de volgende benaderingen van de
twee hoogtes. Voor de weg:
![]()
Voor de hoogte aan het eind van de wandeling:
![]()
Voor deze laatste benadering doen we twee stappen: de teller wordt R×α2/2=d2/(2R). Nu moeten we nog met 1/(1-α2/2) vermenigvuldigen, maar voor kleine x geldt
![]()
dus vermenigvuldigen we met 1+α2/2 met als resultaat
![]()
Die laatste term is zo klein dat we hem weg mogen laten.
Als we de benaderingen toepassen krijgen we 0.706858347 voor de weg en 113.4114948 voor de wandeling. De verschillen met de antwoorden dan gisteren zijn in de orde van grootte van tienden van milimeters voor de weg en van milimeters voor de wandeling.
Waarom zou je die benaderingen maken? Een rekenmachientje geeft toch meteen een uitkomst, ook met de ingewikkelde formules? Het antwoord is tweeledig. Ten eerste heb je niet altijd een rekenmachine bij de hand en dat worden die formules wat bewerkelijk. Ten tweede, en dat is de eigenlijke reden: aan de benadering kun je vaak beter afzien hoe de uitkomst van de invoer afhangt. In beide gevallen hebben we gezien dat er een kwadratisch verband is: de grafiek van h als functie van w of d is nagenoeg een parabool.
Een ander voorbeeld van het werken met benaderingen is te vinden in dit artikel uit Pythagoras:
Een touwtje om de aarde.
Tot slot wat opdrachten.
Opgave 1. Bereken d4/(4R3); was het gerechtvaardigd die term weg te laten?
Opgave 2. Ga na dat de benadering ook werkt voor de diepte van de ingegraven weg.
Opgave 3. De benadering zijn, natuurlijk, niet exact. Ga na of ze de echte waarden over- of onderschatten (ook voor de ingegraven weg).
Opgave 4 Onderzoek hoe goed de benadering 1+x van 1/(1-x) is.

Recent Comments