Posted in July 2017
KP checkt: 0,004 voetbalvelden
Je moet het eigenlijk niet doen, een grap narekenen. Maar toch, De Speld berichtte over een fenomenale prestatie van Harm, die 20 m2 kliklaminaat had gelegd, ruim 0,004 voetbalvelden. Ik heb dat getal toch even geverifieerd.
Na enig zoeken vond ik op de website van de KNVB een document met op pagina 10 een plaatje van een standaard voetbalveld. De lengte van een veld mag variëren van 100 tot 105 m en de breedte van 64 tot 69 m.
Dan zijn we er snel uit: de oppervlakte van een officieel voetbalveld is minimaal 6400 m2 en maximaal 7245 m2. Even cijferen (of een rekenmachientje) leert ons het aantal voetbalvelden dat Harm aan kliklaminaat gelegd heeft tussen de 0,00276 en 0,003125 ligt, Nederlandse voetbalvelden dan.
Internationaal zit er nogal wat speling in de afmetingen van voetbalvelden. Volgens de IFAB website mag de lengte van een veld liggen tussen 90 en 120 m en de breedte tussen 45 en 90 m. Voor internationale wedstrijden is het wat strakker geregeld: lengte van 100 tot 110 m, en breedte van 64 tot 75 m. Bij geschikte keuze van lengte en breedte kan Harm dus inderdaad claimen dat hij ruim 0,004 voetbalvelden aan laminaat heeft gelegd.
Ik ben het overigens wel met deze Wikipedia-pagina eens:
Het voetbalveld wordt ook wel als oppervlaktemaat gebruikt, bedoeld voor mensen die hectare (ha) of vierkante kilometer (km2) te abstract vinden. Het kleinste FIFA-veld past tweemaal in het grootste, dus is een “voetbalveld” geen betrouwbare maat.
Opgave
Harm moest het laminaat ook drie trappen op sjouwen; controleer zijn bewering dat als hij dat nog 30,7 miljoen keer had gedaan hij de afstand tot de maan had afgelegd.
Een `rekenprobleem’
Er gaat weer een vraag het internet rond en de discussies lopen weer hoog op. Hier is de som

De meest gegeven antwoorden zijn 9 en 1; die komen van de volgende twee interpretaties van 6÷2(1+2):
- 6÷2×(1+2), gelezen van links naar rechts, dus 6÷2 bepalen en dan vermenigvuldigen met (1+2)
- 6÷(2×(1+2)), dus eerst 2×(1+2) bepalen en dan 6 daar door delen
Welk van de twee is de juiste? Eigenlijk geen van beide omdat het hier om een afkorting gaat waarvan niet duidelijk is hoe die gelezen moet worden.
Hoe dat zo? Welnu, in de (elementaire) rekenkunde hebben we een paar bewerkingen: optellen aftrekken, vermenigvuldigen, en delen. Als we een som opschrijven dan kunnen we die ondubbelzinnig houden door middel van haakjes: (1+2)×3 betekent iets anders dan 1+(2×3). Als we heel strikt te werk gaan moeten we zelfs ((1)+(2))×(3) en (1)+((2)×(3)) schrijven; de reden is dat + en × twee argumenten nemen en door (al) die haakjes word precies duidelijk wat die argumenten zijn.
De mens is lui en wil al die haakjes niet opschrijven en daarom is bedacht/afgesproken dat × en ÷ sterker binden dan + en -, dus 1+2×3=7 omdat we hebben afgesproken dat 2×3 eerst moet worden bepaald en dan pas de optelling. Wat als er even sterk bindende symbolen achter elkaar staan? Van links naar rechts werken zeggen de officiële voorschriften (pagina 20), dus 4÷2×4=8: eerst 4÷2=2 en dat vermenigvuldigen met 4; er staan dus impliciete haakjes: (4÷2)×4.
Maar de mens is nog luier en heel vaak wordt een × weggelaten, bijvoorbeeld in onze som: 2(1+2) staat voor 2×(1+2). Als we die × weer invoegen en de regel “van links naar rechts” volgen komen we uit op 9. Echter, en daar ontstaat de verwarring, sommige mensen vinden dat een weggelaten × sterker bindt dan een expliciete × of ÷; dat is niet een officiële afspraak maar een ingesleten gewoonte. En dan lezen we de som als 6÷(2×(1+2)), met als uitkomst 1.
Wat is de oplossing? Wat mij betreft: de vraag terugkaatsen met “Wat bedoel je?” Als ik zou moeten kiezen dan toch maar het eerste antwoord: × invoegen en dan van links naar rechts werken.
Hieronder een paar antwoorden van rekenprogramma’s en rekenmachienes.
Het beste antwoord komt van het programma bc:
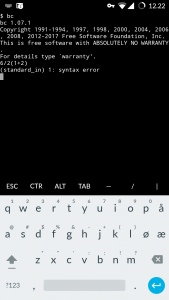
De QAMA-calculator doet gewoon niks; als ik de som intik gaat de cursor weer naar het begin van de regel.
Maple lijkt (1+2) gewoon te negeren
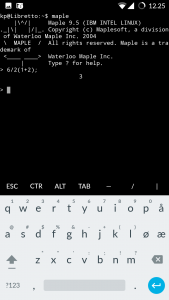
De calculator in mijn telefoon (Android) geeft 9 als antwoord; onderweg wordt 6÷2 uitgerekend, en (1+2) leidt tot een vermenigvuldiging.
En als je niet van haakjes houdt kun je altijd nog dc gebruiken of een andere calculator die met `reverse Polish notation’ werkt:
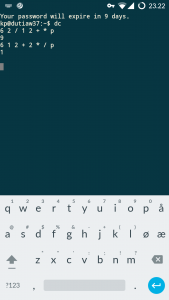
Het echte verhaal
En voor wie echt tot op de bodem wil gaan: delen bestaat niet, 6÷2 is een afkorting van 6×2-1, waarbij 2-1 de multiplicatieve inverse van 2 is (2-1 is een afkorting voor “dat getal, x, met de eigenschap dat 2×x=1”).
De vraag is dus of de som vraagt naar 6×2-1×(1+2) of naar 6×(2×(1+2))-1.
En eigenlijk zijn × en + ook afkortingen, in de echte officiële wiskunde zouden we alles in gewone functienotatie op moeten schrijven: v(a,b) in plaats van a×b, o(a,b) in plaats van a+b, en i(a) in plaats van a^{-1}. De mogelijke interpretaties van de som worden dan respectievelijk v(v(6,i(2)),o(1,2)) en v(6,i(v(2,o(1,2)))).
(On)zinnige vragen
Op 9 juni 2017 stond er een mooi stuk van Ellen de Bruin in NRC over de leeftijden van haar en haar moeder; die waren namelijk elkaars omgekeerde: 47 en 74. Tijdens het schrijven van dat stuk vroeg Ellen mij mee te denken over wat een vraag zinnig maakt.

Zoals in de krant beschreven deed ik dat denken op de fiets en aangezien ik elke dag naar en van het werk fiets kwam ik af en toe ook weer terug op het begrip `zinnige vraag’. Een beroemd wiskundige hield een groep studenten voor: “there are no stupid questions” en presteerde het bij de eerste vraag uit de zaal te zeggen “Now, that is a stupid question”.
Ik ben het met beide bovenstaande uitspraken eens: in principe is elke vraag zinnig want er spreekt, hopelijk, een wens uit meer te weten, en dan is altijd een goede zaak. Aan de andere kant: als een student op de universiteit zich afvraagt of √(x+y) toch niet gelijk is aan √x+√y dan is dat in die context een onzinnige vraag want die student zou beter moeten weten.
Of een vraag zinnig is hangt dus vaak van de context af; voor wie net heeft geleerd wat worteltrekken is is het verband tussen √(x+y) en √x+√y iets nieuws.
Het artikel van Ellen de Bruin had te maken met de speciale schrijfwijze die wij hanteren om getallen boek te houden, en juist die schrijfwijze maakte mogelijk dat er iets met de leeftijden van Ellen en haar moeder aan de hand was. Als we de, nogal omslachtige, de unaire schrijfwijze voor getallen zouden gebruiken dan zagen de leeftijden er zo uit: |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| en |||||||||||||||||||||||||||||||||||||||||||||||. Daar is niet veel bijzonders aan af te zien.
Echter, onze decimale positionele schrijfwijze, met cijfers voor en achter de komma, is er zo bij ons ingebakken dan mensen nog wel eens vergeten dat het niet meer is dan een schrijfwijze. Er zijn vele manieren in gebruik (geweest) om getallen boek te houden en de huidige Indo-Arabische heeft gewonnen omdat deze op het juiste moment door veel handelaren en wetenschappers gebruikt werd. Maar omdat de schrijfwijze nu eenmaal universeel gebruikt vereenzelvigen veel mensen getallen met die ene schrijfwijze. Dat is normaal gesproken niet erg, “het getal 21” is een stuk korter dan “het getal dat in de Indo-Arabische schrijfwijze wordt weergegeven als 21” maar het kan in de wiskunde leiden tot vragen die echt onzinnig zijn.
Sommige mensen lijken te denken dat de rijen cijfers fysieke entiteiten zijn die je beet kunt pakken, op kunt tillen, en ergens anders neer kunt zetten. Een aantal jaren geleden stuurde iemand mij de volgende vraag: “Is het wiskundig toegestaan de oneindig veel negens in 0,999999… in omgekeerde volgorde vóór de komma te zetten?” Ik parafraseer want in de tussentijd is bij een niet-geplande schoonmaak van mijn harde schijf nogal wat email verloren gegaan. Wat ik toen terug had moeten schrijven is dat dat een onzinnige vraag is en wel hierom.
De uitdrukking 0,999999… is een informele manier om het volgende samen te vatten (af te korten): wij nemen de functie, f, van de verzameling N der natuurlijke getallen naar {0,1,2,3,4,5,6,7,8,9}, die voor elke n voldoet aan f(n)=9 en we maken daarbij een reëel getal door de termen van de rij f(1)×10-1, f(2)×10-2, … f(n)×10-n, … op een welbepaalde menier bij elkaar op te tellen.
Het onzinnige van de vraag ligt hem in die achtergrond: een informele afkorting van een niet geheel triviaal stukje wiskunde wordt omgebouwd tot een nieuwe afkorting van … van wat eigenlijk? In ieder geval niet van een of ander natuurlijk getal. In plaats van meteen te zeggen dat dit onzinnig was heb ik geprobeerd door tegenvragen de vraagsteller dit zelf in laten zien; dat is niet gelukt. Hij wilde op deze manier een bijectie tussen N en het interval [0,1] maken en mijn vragen leidden daar alleen maar van af.
Rare Vragen, III
In de serie `Rare Vragen uit de wisfaq‘ vandaag een non-vraag.
Hier is de hele `vraag’
Bepaalde lijnintegraal die de wortel van π als uitkomst geeft
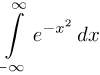
Het gebeurt wel vaker: een uitdrukking of vergelijking zonder verder commentaar, maar met de impliciete vraag (een bevel?) om een uitwerking.
Ik kon het niet helpen; ik heb geantwoord met de beroemde voetnoot uit The Life of Lord Kelvin die een wiskundige beschrijft als iemand voor wie de waarde van die integraal net zo duidelijk is als 2+2=4. Zie bijvoorbeeld dit artikel uit de Bulletin of the American Mathematical Society
Rare vragen, II
In de serie `Rare vragen uit de wisfaq‘ vandaag een verschijnsel dat
gemengde gevoelens bij me oproept.
Hier is een voorbeeld
Re: Deelbaarheid door 11
Voor een onderzoekscompetentie zou ik graag iets doen met de deelbaarheid van getallen. Ik wilde een bewijs opstellen voor de deelbaarheid van het getal 11. Hiervoor heb ik dan volgende formule gekregen.Ik heb ondertussen al ondervonden wat een sommaties en modulo zijn maar snap nog de formule nog steeds niet goed. Zou iemand me kunnen helpen aub?
Het `Re:’ in de vraag geeft aan dat het om een reactie op een antwoord op een eerdere vraag gaat, in dit geval een vraag van de vraagsteller zelf. Hoewel de genoemde `volgende formule’ niet te zien is, gaat het waarschijnlijk om de regel die in het eerdere antwoord gegeven is.
Het verschijnsel waar ik op doelde zit besloten in het woord `onderzoekscompetentie’. De leerling moet kennelijk iets onderzoeken. En dat gebeurt, zo te zien, niet door met `deelbaarheid door 11′ op Google te zoeken (ruim elfduizend treffers) maar door een vraag op een forum te stellen. De eerste vraag klonk nog als een vraag, en kreeg een passend antwoord (al zeg ik het zelf); de follow-up hierboven noemde het onderzoeksaspect maar was passief van toon. Mijn tweede antwoord was een zoekopdracht op de wisfaq; er is heel wat te onderzoeken onder die ruim negentig treffers.
Het komt iets minder vaak voor dan een paar jaar geleden (zegt mijn natte vinger) maar zo af en toe is er weer een vraag die klinkt als: “ik moet/wil een (profiel)werkstuk over onderwerp X maken, kunt U mij onderwerp X uitleggen? Of: kent U websites die wat over onderwerp X zeggen?”
Dat leidt dus tot gemengde gevoelens: je kunt zoiets op een paar manieren lezen/interpreteren: als een vraag het denkwerk voor de leerling te doen of als een echte vraag om hulp omdat de leerling niet weet wat te doen. In het eerste geval wordt ik wat knorrig maar stuur ik de leerling met wat zoektips op weg. In het tweede geval ook, maar de knorrigheid richt zich dan (terecht of niet) op meer dan één doel: de leerling die niet het benul heeft een zoekmachine aan te zetten; de leerkracht die de leerling het bos in stuurt; of het `idee’ dat leerlingen van nature alles willen, en dus zullen, leren. Ik weet niet wie het uiteindelijk verdient maar ik krijg wel door, ook bij het begeleiden van bachelorprojecten, dat het lang nodig blijft leerlingen en studenten duwtjes in de goede richting te geven.
Rare vragen, I
Ik heb hier al een paar keer geschreven over vragen die ik voor de wisfaq beantwoord heb. De wisfaq is een prachtig initiatief en Willem van Ravenstein verdient alle lof voor het oprichten en onderhouden van die website. De Koninklijke Bibliotheek heeft zelfs besloten dat de site een deel van ons `digitaal erfgoed’ is en is begonnen de website te archiveren.
De meeste vragen zijn vragen om hulp bij het huiswerk maar soms is er een vraag waar even over nagedacht moet worden en een enkele vraag heb ik zelfs bij mijn eigen onderwijs kunnen gebruiken.
Maar sommige vraagstellers trekken zich weinig van de spelregels aan. Eén van die regels is “wees duidelijk”. De volgende vraag voldeed daar niet echt aan.
Onder de kop Analytische Meetkunde staat het volgende
twee vragen!
1. De parameter van de ellips is : p = b kwadraat : a ;
heel graag de berekening .
2. de namen : ellips is minder dan iets , parabool is gelijk aan iets en hyperbool is meer dan iets. Wat is dit iets ?
Dat was alles …
De tweede vraag had ik als eens beantwoord in Pythagoras, maar van vraag 1 kon ik niets maken. En eigenlijk wilde ik er niets van maken want het was niet eens een volledige zin. Een vraag om nadere informatie leverde de volgende `verduidelijking’
p is loodlijn uit F op lengte-as tot snijpunt met ellips
a is halve lengte-as, b is halve breedte-as
Ik dacht dat jullie dit wel begrepen hadden :Sorry !
Denkt iedereen echt dat wiskundigen helderziend zijn?
Snel ordenen
Nog een vraag van de wisfaq:
Ik ben me aan het voorbereiden voor toelatingsexamen aan de Koninklijke Militaire School en kwam volgende vraag tegen:
Sorteer a, b en c volgens stijgende waarden: a=√23; b=1199/250; c=959/200
Nu vroeg ik me af hoe ik dit efficiënt kan doen en zonder rekenmachine weliswaar!
Hoe doe je zoiets snel? Als ik veel haast heb bereken ik misschien 1199×200 en 959×250. Er geldt namelijk dat b>c precies als 1199×200>959×250 (via kruislings vermenigvuldigen) en daarnaast zou ik snel de kwadraten van b en c bepalen en met 23 vergelijken.
Die vermenigvuldigingen kosten wel wat tijd want de getallen zijn een beetje groot. Daarom kan het handig zijn iets beter naar de getallen te kijken. Dan blijkt dat die twee breuken hetzelfde gehele deel hebben, namelijk 4, en dat wat overblijft snel te vergelijken is:
1199/250=4+199/250=4+796/1000 en 959=4+159/200=4+795/1000 en nu zijn b en c in ieder geval heel eenvoudig te vergelijken: b>c.
En hoe zit het met √23? Het kwadrateren van b en c kan iets sneller als je het indirect doet: schijf b=5-204/1000 en c=5-205/1000, en gebruik de bekende formule (x-y)2=x2-2xy+y2. Dan blijkt dat
- b2=23-4/100+(204/1000)2, en
- c2=23-5/100+(205/1000)2.
Nu is (204/1000)2 net iets meer dan (2/10)2=4/100, dus b2 is net iets groter dan 23.
Ook (205/1000)2 is iets meer dan 4/100 maar niet te veel: het is kleiner dan het makkelijkere kwadraat (21/100)2=4,41/100 en dat is weer kleiner dan 5/100, dus c2 is kleiner dan 23.
Conclusie: 959/200<√23<1199/250.
Ik vind dit een aardige opgave omdat met weinig niet al te moeilijke vermenigvuldigingen en delingen drie getallen die heel dicht bij elkaar liggen toch mooi onderscheiden kunnen worden.
Tien getallen rond een tafel
Op de Wisfaq stond laatst weer een aardige vraag:
Natuurlijke getallen van 1 tot en met 10 zijn geordend in een willekeurige volgorde rond een cirkel. Je kan steeds (dus in een cirkel is er minstens 1 geval) 3 opeenvolgende getallen vinden waarvoor de som groter is dan 17.
Hoe zou je zoiets aanpakken? Meestal kun je wel iets over die sommen zeggen waardoor blijkt dat er één (of meer) over een bepaalde grens moet gaan, bijvoorbeeld als de som van al die sommen groot moet zijn.
In dit geval kunnen de tien sommen bij elkaar optellen; dan tellen we elk getal 1, 2, …, 9, 10 driemaal mee dus we krijgen als totaal 3×(1+2+…+9+10)=3×55=165.
Dat betekent dat niet alle sommen kleiner dan 17 kunnen zijn, want dan zou hun totaal niet groter zijn dan 10×16=160. Het eerste succes is binnen: we zien vrij goedkoop dat tenminste één drietal een som van 17 of meer moet hebben.
Vervolgens heb ik een paar vellen kladpapier gebruikt om de getallen zo rond de tafel te plaatsen dat alle sommen niet groter waren dan 17. Waarom? Voor mij is het zo dat als ik zoiets vaak genoeg mis zie lopen ik een idee krijg hoe te bewijzen dat het gevraagde waar is: de reden van het mislopen is soms een sleutel tot een bewijs.
In dit geval bleek het lastig het gemiddelde van de sommen in de buurt van 16,5 te houden, dus ging ik kijken hoe dat gemiddelde gelijk kon zijn aan 16,5 terwijl alle sommen niet groter dan 17 mochten zijn.
Na wat proberen bleek dat ten minste vijf van de sommen gelijk aan 17 moeten zijn; immers, bij vier (of minder) sommen gelijk aan 17 zijn de andere zes (of meer) sommen niet groter dan 16 en dus zou het totaal niet groter zijn dan 4×17+6×16=164, en dat is net te klein.
Daarnaast bleek dat er ook maar ten hoogste vijf sommen gelijk aan 17 konden zijn. Dat was zo duidelijk dat ik het eerst over het hoofd zag: neem vier getallen op een rij: x1, x2, x3, x4.
Omdat x1≠x4 volgt dat x1+x2+x3≠x2+x3+x4. Van elk tweetal naast elkaar liggende sommen is er dus hooguit één gelijk aan 17.
Als we de tafel rondlopen zien we dus nooit twee sommen gelijk aan 17 naast elkaar; dat betekent dat we niet meer dan vijf maal een 17 zullen zien.
Nu weten we dat er precies vijf sommen gelijk zijn aan 17, maar dan moeten de andere vijf sommen gelijk zijn aan 16 (om het totaal op 165 te houden) en de sommen 17 en 16 komen dus om en om voor.
Loop nu de tafel rond en noem de getallen die je ziet x1, x2, … en begin op een plek waar x1+x2+x3=17. Dan moet vervolgens gelden
- x2+x3+x4=16, en
- x3+x4+x5=17, en
- x4+x5+x6=16, en
- x5+x6+x7=17.
Trek de tweede vergelijking van de eerste af, je ziet x1-x4=1.
Trek de vierde vergelijking van de vijfde af, je ziet x7-x4=1.
Maar nu volgt x1=x7 en dat kan niet want we hadden tien verschillende getallen rond de tafel gezet.
Conclusie: elke poging alle tien de sommen kleiner dan of gelijk aan 17 te houden zal falen. Hoe je de getallen ook neerzet, er is een som die groter is dan 17.
In de Wiskunde heet zoiets een (niet-constructief) existentiebewijs: we laten zien dat iets moet voorkomen maar er is geen recept dat het gewenste verschijnsel aanwijst. Het bewijs geeft (slechts) aan hoe een poging zal stranden: je moet vijf keer 17 als som hebben, en vijf keer 16, en die moeten om en om voorkomen en dan loopt het echt mis: twee verschillende getallen moeten gelijk zijn.
Opdracht.
Om te puzzelen: is er een verdeling met alle sommen niet groter dan 18? Ik heb het nog niet geprobeerd.
Twee machten vergelijken
Op een paar plekken op het web dook de vraag weer eens op wie groter is: 10001001 of 10011000.
Je kunt die vraag op meer dan één manier/niveau beantwoorden. Achtereenvolgens bekijken we
- Rekenmachientje: neem links en rechts de duizendstemachtswortel en vergelijk 10001,001 met 1001. Dank aan Frank Boers (via `Leraar Wiskunde’ op Facebook).
- Logaritmen en rekenmachientje: de logaritmen (basis 10) kunnen eenvoudig vergeleken worden en we krijgen informatie over het aantal cijfers in beide machten.
- Natuurlijke logaritmen en integralen: de natuurlijke logaritmen van de machten kunnen, met een beroep op een eenvoudige eigenschap van de integraal `met de hand’ vergeleken worden.
- Binomium van Newton: schrijf (1000+1)1000 uit met behulp van het binomium en laat zien dat de termen in de som steeds groter worden; hiermee is de macht snel af te schatten.
- Binomium van Newton (bis): het quotient van (1000+1)1000 en 10001001 is met behulp van het binomium af te schatten met 3/1000.
- Het getal e: met behulp van een definierende rij voor e kan de vorige afschatting verbeterd worden tot e/1000.
- Functieonderzoek: in het algemeen geldt: als e<x<y dan yx<xy. Dit volgt door de functie x/ln(x) te bekijken. Dank aan René Pannekoek.
- Gebruik de e-macht: via ex>1+x vind je 10001,001>1000+ln(1000).
De oplossingen vereisen nogal wat wiskundige notatie; daarom heb ik ze hier in een PDF-file neergezet.
Sorteren
In haar column van 1 juli beschreef Ionica Smeets hoe de logistiek van een menselijke keten van de Belgische kerncentrale Tihange naar de Duitse stad Aken haar aan van alles deed denken, behalve kernenergie.
Een van de problemen die bij haar opkwam was het op alfabet sorteren van de schakels in de mensenketen en hoe lang dat zou duren. De sorteermethode waar ze aan dacht bestaat uit het telkens vergelijken van de namen van twee naast elkaar staande personen en die, indien nodig, omwisselen.
Nu kun je zoiets op veel manieren uitvoeren en zo ongeveer het eerste sorteerprogramma dat ik zelf geschreven heb loopt telkens van begin tot eind door de lijst en wisselt verkeerd geordende buren om. Hier is een versie in de taal python (de n is de lengte van de lijst; in python wordt een lijst van lengte n genummerd van 0 tot en met n-1):
for k in range(1,n-1):
for l in range(1,n-k):
if x[l] < x[l-1]:
xx = x[l]
x[l] = x[l-1]
x[l-1] = xx
Het programma is iets versneld: als k=1 staat aan het eind van de binnenste loop het grootste element in x[n-1]; als k=2 staat aan het eind van de binnenste loop het op één na grootste element in x[n-2], enzovoort. Dit betekent dat er slechts n-1 binnenloops uitgevoerd hoeven worden die ook steeds korter worden: l loopt telkens maar tot n-k.
Hoe lang duurt het voor het programma klaar is? Neem aan dat we het alfabetisch van Aken naar Tihange willen sorteren. In het ergste geval, als de lijst al alfabetisch gesorteerd is maar net andersom, van Tihange naar Aken dus, moeten er 50000×49999/2 verwisselingen gedaan worden. Dat zijn er, afgerond, 1,25×109, (veel) meer dan een miljard dus.
Aangenomen dat een verwisseling een seconde kost dan zijn we met mijn programmaatje wat meer dan 39 jaar bezig.
Efficiënter?
Het bovenstaande programmaatje implementeert het zogeheten bubble-sort (de grotere elementen `borrelen’ omhoog door de lijst). Bedenk dat dit bij onze mensenketen neerkomt op het volgende: de hoofdorganisator holt iedere keer keer weer langs de keten mensen en laat telkens verkeerd geordende tweetallen omwisselen. Hierbij staat iedereen vrijwel de hele tijd te niksen.
We kunnen die mensen beter zelf wat laten doen door ze als parallelle processoren te gebruiken. Op elk moment laten we de mensen die dan op een evengenummerde plaats staan zich met een buur vergelijken en, zo nodig, van plaats verwisselen. Op de oneven momenten kijken die mensen richting Tihange en op de even momenten richting Aken.
Dus bij stap 1 laten we alle paren (0,1), (2,3), (4,5), … (49998,49999) vergelijken en, indien nodig, wisselen. Bij stap 2 laten we dat de paren (1,2), (3,4), (5,6), … (49997,49998) doen. Dit gebeurt om en om tot de rij gesorteerd is. Dit proces staat, om een voor de hand liggende reden, bekend als odd-even sort.
Omdat we nu telkens 25.000 verwisselingen tegelijk laten doen kost dit `maar’ 50.000 iteraties. En als iedereen goed meewerkt zijn we dus in 50.000 seconden klaar, dat is wat minder dan 14 uur.

Recent Comments