Posted in 2017
KP zag een gat
Op twitter raakte ik betrokken in een discussie over gaten, in het bijzonder over het aantal gaten dat een rietje heeft. Het antwoord hangt natuurlijk af van wat je als `gat’ aanmerkt maar als je er wiskundigen (in dit geval Ionica Smeets en mij) bij haalt dan krijgt je `één’ als antwoord. En dat komt omdat wiskundigen precies hebben afgesproken wat een `gat’ is en die afspraak leidt tot dat antwoord.
Wat is een gat dan?
We (de wiskundigen dan) beschouwen het rietje als een oppervlak en we tellen de gaten in dat oppervlak door vanuit een vast punt op dat oppervlak krommen te tekenen die beginnen en eindigen in dat punt. Dat is wat lastig met een fysiek rietje dus nemen we een rietje van een heel elastisch materiaal en door het aan één kant op te rekken kun je er een ringvormig gebied in het platte vlak van maken. Het tekenen gaat daar wat makkelijker; je kunt de krommen met touwtjes of elastiekjes maken; dat scheelt uitgummen als het papier te vol wordt.
Bij sommige krommen kun je het elastiekje laten krimpen tot het zo klein is als het vaste punt en zonder dat het elastiekje buiten het werkgebied komt. Bij andere lukt dat niet, bijvoorbeeld één keer (tegen de klok in) om het binnengebied gaat (of twee keer, of drie keer, …).
Een kromme die niet tot het vaste punt samengetrokken kan worden zonder buiten het werkgebied te komen wijst, wiskundig gesproken, op een gat. Dit betekent niet dat we vinden dat er oneindig veel gaten in het gebied zitten. Je kunt namelijk bewijzen (en dat kost enig werk) dat elke kromme (elastiekje) vervormd kan worden tot die ene kromme die één keer linksom het binnengebied gaat; daarbij wordt het aantal keren dat de kromme om het binnengebied gaat bewaard.
Dus een kromme die drie keer om het binnengebied gaat kun je vervormen tot drie keer achtereen die ene kromme, met behoud van richting.
Omdat elke kromme eigenlijk een aantal keer de ene basiskromme doorloopt vinden we dat het gebied één gat heeft.
Een T-stuk
Verderop in de twitterlijn kwam dit plaatje tevoorschijn: een bouwsel van twee rietjes dat eigenlijk een T-stuk voorstelde. Nu heeft een T-stuk drie openingen maar wiskundig gesproken zijn er maar twee gaten. Dat is met de nieuwe grens van 280 karakters net in één tweet uit te leggen:
Buig gaten 1 en 3 naar links zo dat je een broek krijgt; krimp de pijpen in tot je een zwembroekje overhoudt. Leg het broekje op tafel waarbij je gat 2 onder houdt en zover oprekt dat het de buitenrand wordt. Strijk alles glad: cirkelschijf met twee gaten.

Er zijn nu twee basiskrommen: neem een punt ergens in het midden en teken een kromme die één keer om het linkergat gaat en één keer om het rechtergat (beide tegen de klok in).
Elke andere kromme die in het gekozen punt begint en eindigt is te vervormen tot eentje die de basiskrommen doorloopt. Hierbij is het wat ingewikkelder dan bij één gat. De volgorde is van belang: eerst links dan rechts is niet hetzelfde als eerst rechts dan links.
Dus: twee basiskrommen en daarmee twee gaten.
Gaten in de kaas
Gaten (bubbels) in de kaas kun je niet met krommen detecteren: je kunt elke kromme tot een punt vervormen buiten alle holtes om. In dat geval gebruikt men (virtuele) ballonnen: een ballon waar een gat binnen ligt kun je niet geheel binnen de kaas samentrekken. Je kunt zelfs `basisballonnen’ definiëren en laten zien dat elke andere ballon tot een combinatie van basisbalonnen te vervormen is maar dat afspreken is een stuk ingewikkelder dan bij het doorlopen van krommen.
On this day in 1873, II
A little over a week ago I wrote about a letter from Cantor to Dedekind that contained an auspicious question, namely whether the sets of natural and (positive) real numbers could be put into one-to-one correspondence with each other.
On 7 December 1873 Cantor wrote Dedekind with the answer to his question; the answer was (and still is) “no”. The letter contains a proof of the impossibility of a one-to-one correspondence between the two sets.
This was the first time that something like this was done: attempt to compare two infinite entities by pairing off the elements of the sets such that every element of the first was paired with exactly one from the second and vice versa.
Cantor went on to study this idea in depth and he showed how to give a precise meaning to the idea that one set has (strictly) more (or fewer) elements than another set.
To get back to the original question: it is clear that there are at least as many real numbers as there are natural numbers as the latter set is a subset of the former. Cantor’s proof showed that there are strictly more real numbers than there are natural numbers.
There is a difference between this situation and the one mentioned in Cantor’s letter of 29 November, 1873: he mentioned that the natural numbers also form a subset of the positive rational numbers (all fractions of the form p/q with natural numbers p and q). Thus, it seems that there are more such rational numbers than that there are natural numbers. But, we can pair off the members of both sets in such a way that to one member of one set corresponds exactly one member of the other set.
To see this divide the fractions into groups: put fraction p/q into group n if p+q=n. Now observe that group n contains exactly n-1 fractions: 1/(n-1), 2/(n-2), …, (n-1)/1. This makes it easy to arrange the fractions in a nice simple sequence: first group 2, then group 3, then group 4, and so on and inside each group arrange the fractions according to their numerators, as we did above in group n.
The resulting sequence looks like this: 1/1, 1/2, 2/1, 1/3, 2/2, 3/1, 1/4, 2/3, 3/2, 4/1, … and this makes it easy to pair off the natural numbers and the positive fractions as desired.
Exercise Try to devise a formula for the number that goes with the fraction p/q, or, conversely, concoct a formula that tells us what the nth fraction is.
Exercise What would you do if you had to pair off the natural numbers and the positive rational numbers (one rational number corresponds to many fractions).
Here you can read Cantor’s letter in German. It is a scan from Briefwechsel Cantor-Dedekind. And here you can read my translation into English.
On this day in 1873
On this day, 29 November, in 1873 Georg Cantor wrote a letter to Richard Dedekind. It contained a question that inaugurated a new mathematical discipline: Set Theory.
Cantor writes:
Allow me to put a question before you that is of some theoretical interest to me, but which I have not been able to answer; maybe you can, and would you be so kind as to write me about this, it concerns the following.
One takes the aggregate of a positive whole numbers n and denotes this by (n); furthermore one considers the aggregate of all positive real numbers x and denotes this by (x); then the question is simply that whether (n) and (x) can be put into some correspondence in such a way that every individual from one aggregate belongs to just one of the other and conversely?
In modern terms: is there a bijection between the set of natural numbers and the set of positive real numbers?
Cantor goes on to say that a simple `no’ “because (n) is discrete and (x) forms a continuum” does not suffice because the same could be said of (n) versus the aggregate of positive rational numbers yet one can create a correspondence as desired between these two entities.
The full letter can be read here in German. It is a scan from Briefwechsel Cantor-Dedekind.
The answer to the question? Watch this space.
Het Sinterklaasprobleem
Het probleem van vandaag is niet dat van de kleur van de knechten van de Goedheiligman maar dat van het trekken van de lootjes. Wat is de kans dat dat in één keer goed gaat? Kun je het in één keer goed laten gaan?
De kans dat het goed gaat
Als je de namen van alle deelnemers op een papiertje schrijft en daarna iedereen een papiertje uit de hoed (o.i.d.) laat trekken wat is dan de kans dat niemand zichzelf trekt?
Om die kans te kunnen bepalen moet je twee dingen tellen: het totaal aantal manieren waarop de papiertjes uit de hoed getrokken kunnen worden èn het aantal gunstige mogelijkheden. Het laatste aantal gedeeld door het eerste geeft dan de gewenste kans.
Als je dit wiskundig aan wil pakken maak je de situatie zo eenvoudig mogelijk: zet de mensen op een rij, en nummer ze: 1, 2, …, n. Na de trekking zet je persoon i op de plaats van degene die haar getrokken heeft. Op die manier komt een trekking overeen met het op één of andere volgorde zetten van de getallen 1, 2, …, n. Een gunstige trekking is er één waarbij elk getal van zijn (natuurlijke) plaats gehaald wordt.
Je kunt voor kleine n de tellingen met de hand uitvoeren maar het wordt al gauw een beetje onoverzichtelijk: de gevallen n=1 en n=2 zijn een beetje triest, die slaan we maar over. Bij n=3 kunnen we zes trekkingen uitvoeren (schrijf de volgordes maar eens op) en daarvan zijn er twee gunstig: (2,3,1) en (3,1,2). De kans dat het goed gaat is dus 1/3.
Bij een groep van vier mensen zijn er 24 mogelijk trekkingen: de eerste kan vier papiertjes trekken, de tweede drie, de derde twee en de laatste één. Dat levert 4×3×2×1=24 mogelijke volgordes. Het aantal gunstige mogelijkheden is wat lastiger te tellen: je kunt 1 en 2 omwisselen en ook 3 en 4, of 1 en 3 en ook 2 en 4, of 1 en 4 en ook 2 en 3. Dat geeft drie mogelijkheden. Je kunt de getallen ook doorschuiven: zet de mensen in een kring en laat iedereen een positie (naar links) opschuiven; we zetten 1 telkens op dezelfde vaste plek en zetten de andere drie willekeurig neer en dat levert nog zes mogelijkheden. In totaal 9 gunstige rangschikkingen met kans 9/24, ofwel 3/8.
Wie wil puzzelen kan proberen het aantal gunstige rangschikkingen uit de in totaal 5×4×3×2×1=120 manieren om vijf mensen te plaatsen te tellen maar dat wordt al behoorlijk bewerkelijk.
Inclusie-Exclusie
Er is een manier om de telling van het aantal gunstige manieren systematisch te tellen en die manier is ook op veel andere problemen toepasbaar. Het blijkt makkelijker het aantal ongewenste trekkingen te tellen.
Neem een getal n en bekijk de verzameling {1,2,…,n}. Die verzameling kan op n×(n-1)×…×1 manieren gerangschikt worden (het argument hierboven voor n=4 blijft van toepassing). Dat getal noteren we met n! (spreek uit: n-faculteit).
Voor iedere i noteren we de verzameling rangschikkingen die i op haar plaats laten met Di. We willen dus tellen hoeveel elementen er in de vereniging D1∪D2∪…∪Dn zitten.
Voor het gemak voeren we nog de notatie |X| voor het aantal elementen van de verzameling X in.
Teken een plaatje met twee verzamelingen, zeg X en Y, en ga na dat we |X∪Y| als volgt uit kunnen drukken:
|X∪Y|=|X|+|Y|-|X∩Y|
immers: in de som |X|+|Y| tellen we de punten in X∩Y dubbel en daarom moeten we |X∩Y| aftrekken.
Teken een plaatje met drie verzamelingen, X, Y en Z, (met alle mogelijke doorsneden er in) en ga na dat
|X∪Y∪Y∪Z|=|X|+|Y|+|Z|-(|X∩Y|+|X∩Z|+|Y∩Z|)+|X∩Y∩Z|
immers: in |X|+|Y|+|Z| tellen we |X∩Y|+|X∩Z|+|Y∩Z| dubbel, dus dat trekken we af; maar nu zijn de punten in X∩Y∩Z drie keer meegeteld en drie keer afgetrokken, daarom tellen we |X∩Y∩Z| weer op
Als we dit toepassen op het geval n=3 dan krijgen we
|D1|+|D2|+|D3|-(|D1∩D2|+|D1∩D3|+|D2∩D3|)+|D1∩D2∩D3|
als het aantal ongewenste rangschikkingen; omdat |Di|=2 voor elke i, en omdat |Di∩Dj|=1 als i≠j en omdat |D1∩D2∩D3|=1 vinden we 2+2+2-(1+1+1)+1=4 rangschikkingen waarbij ten minste één punt op zijn plaats blijft. We krijgen dus ons eerder gevonden aantal goede rangschikkingen terug.
In het algemene geval gebeurt hetzelfde: eerst de individuele aantallen optellen, dan twee-bij-twee doorsneden aftrekken, drie-bij-drie doorsneden optellen, vier-bij-vier aftrekken …. Dit heet het Principe van Inclusie-Exclusie.
Er zit veel regelmaat in onze aantallen:
- |Di|=(n-1)! (de andere punten mogen willekeurig gerangschikt worden
- |Di∩Dj|=(n-2)! (de andere punten mogen willekeurig gerangschikt worden
- elke k-bij-k doorsnede heeft (n-k)! elementen
Het aantal k-bij-k doorsneden is gelijk aan n!/(k!×(n-k)!) en dat maakt onze berekening heel overzichtelijk: er zijn
![]()
slechte rangschikkingen en dus
![]()
goede rangschikkingen. Als we dat aantal door n! delen komen we uit op een succeskans van
![]()
bij het lootjes trekken met n personen.
Omdat de termen in de som in absolute waarde steeds kleiner worden en beurtelings positief en negatief zijn volgt dat die kans altijd tussen 1/3 en 3/8 zal liggen.
Altijd succes?
Voor wie wil weten hoe je in één keer een goede trekking kunt verrichten: lees deze column van de Wiskundemeisjes uit 2009.
De methode komt er op neer dat je de deelnemers in een kring zet en hun naambriefjes aan de persoon links laat geven (met een truc om het geheim te houden natuurlijk).
Voor wie van puzzelen houdt: vlooi maar eens uit dat de kans dat er bij willekeurig trekken een permutatie als in die column uit komt gelijk is aan 1/n.
Breien en eenheden
Via een tweet van Ionica Smeets kwam ik op deze pagina van de stichting literaire rechten auteurs (lira). Daar word uitgelegd hoe de uitkeringen voor de auteurs berekend worden.
De berekening verloopt als volgt (citaat):
De puntwaarde maakt onderdeel uit van de berekening van de hoogte van de leenrecht-uitkering. De hoogte van de leenrechtuitkering wordt per titel berekend met behulp van een rekenregel die er per uitgeleende titel als volgt uitziet: A×B=C×D=E.
Heh? Wat? Twee producten die aan elkaar gelijk zijn? Nadere uitleg volgt (citaat):
A staat daarin voor het aantal uitleningen dat blijkens de steekproef-gegevens van een boek heeft plaats gevonden. B staat voor de officiële, aan het ISB-nummer gekoppelde verkoopprijs van het boek, bij gebreke waarvan een forfaitaire prijs wordt ingevoerd, dat wil zeggen: ongeveer de gemiddelde verkoopprijs van het boek in Nederland, tot nu toe steeds afgerond op 25,-. C is het product van A en B en staat voor het aantal punten dat aan deze uitleningen van deze titel wordt toegekend. D staat vervolgens voor het bedrag per punt. Dit bedrag per punt (de puntwaarde) wordt separaat berekend door het totaal aantal binnen de steekproef geconstateerde uitleningen te vermenigvuldigen met de som van alle in het systeem aanwezige verkoopprijzen en de uitkomst daarvan te delen op het totaal van het netto voor uitkering beschikbare bedrag. E tenslotte is het bedrag dat per uitgeleende titel naar gelang het aantal uitleningen en de verkoopprijs als slotsom wordt berekend.
Juist ja, ordinair breiwerk dus: C=A×B en E=C×D, kortom E=(A×B)×D.
Eenheden
Het betrof hier een klacht over vooral die laatste factor D, de puntwaarde, dat begrip werd onduidelijk gevonden. Ik heb de beschrijving van dat ding een paar keer gelezen en ik ben nog niet veel wijzer, ik zie drie dingen
- het totaal aantal binnen de steekproef geconstateerde uitleningen
- dat lijkt verdacht veel op A. Het zou echter ook kunnen zijn dat A een schatting van het totaal aantal uitleningen is, gebaseerd op het onderhavige aantal maar dat had dan wat duidelijker uitgelegd mogen worden.
- de som van alle in het systeem aanwezige verkoopprijzen
- was er een lijst van alle mogelijke bedragen die optreden als prijs van een of ander boek en zijn die bedragen bij elkaar opgeteld? Waarom zou je dat in vredesnaam doen? Ik hoop dat er iets zinvollers werd bedoeld maar ik zou niet weten wat.
- het totaal van het netto voor uitkering beschikbare bedrag
- de woorden `het totaal van’ lijken me hier overbodig
Ik zie hier dus drie grootheden: een aantal, laten we dat n noemen; een bedrag, laten we dat B1 noemen; en nog een bedrag, zeg B2. Uit de beschrijving haal ik dat D gelijk is aan (n×B1)/B2 (of misschien aan B2/(n×B1), want je weet maar nooit wat `delen op’ betekent, ik deel liever door). Maar, hoe dan ook, in tegenstelling tot wat geschreven wordt is de puntwaarde D geen bedrag: D is een dimensieloos getal. De berekening geeft namelijk [getal]×[gulden]/[gulden] (het stuk is uit 2001) en daarin strepen we de guldens tegen elkaar weg.
Ik hoop dat de klager nogmaals geklaagd heeft want deze uitleg was niet best.
Rare vragen IV: vier chemici op zoek naar een optimum (deel 2)
We vervolgen de reis die begon bij deze vraag op www.wisfaq.nl. Inmiddels hebben de studenten aangegeven een docent op te zoeken. Ik had toch nog een paar gedachten over het probleem.
Vierde reactie
Mijn vermoeden was dat de zaak als volgt in elkaar stak: er was een drie-dimensionaal array geïndiceerd met [x1,x2,x3] en bij elk drietal een (meet)waarde y1. Eerst werd bij vaste x2 en x3 door middel van kleinste kwadraten een best passend vierdegraadspolynoom voor y1 in termen van x1 bepaald. De term `kleinste kwadraten’ heb ik er zelf bijgehaald; de studenten hadden het over de `lijnschatter’ van Excel en het klinkt alsof dat een zwarte doos is voor het uitvoeren van lineaire regressie (Google gaf weinig info).
De volgende stap leek dit bij vaste x3 in de in de richting van x2 te herhalen, waarbij coëfficiënten als functie van x2 werden geschreven. En ten slotte werd ook x3 bij het functievoorschrift betrokken.
Ik beschreef dit in mijn reactie en gaf aan dat met kleinste kwadraten ook in één keer een polynoom in drie variabelen voor y1 als functie van x1, x2 en x3 te maken is.
Vijfde reactie
De reactie bevestigde mijn vermoeden maar liet ook zien dat de studenten eigenlijk niet wisten wat ze aan het doen waren: geen reactie op `kleinste kwadraten’.
Voor iemand die weet hoe deze methode werkt is het geen grote stap van één naar meer variabelen. Vermoedelijk is dat niet iets dat makkelijk met de `lijnschatter’ van Excel te doen is.
Zesde reactie
In het (voorlopig) laatste deel van dit verhaal wordt duidelijk dat de studenten toch wel wat wiskunde, in het bijzonder Lineaire Algebra, bij zouden moeten leren.
Conclusie?
Ik werd in het begin op het verkeerde been gezet door de manier waarop de vraag in eerste instantie werd gesteld: het leek of de studenten wisten wat ze deden, uit hun verhaal haalde ik dat ze wisten wat kleinste kwadraten waren maar dat ze niet goed wisten wat met meer dan één variabele aan te vangen. Herhaald toepassen is geen slecht idee maar de beschrijving was zo onduidelijk dat het lang duurde voor ik doorhad dat ze slechts op de zwarte doos die Excel is steunden.
En dan waren we nog niet eens aan de gevraagde optima toegekomen. Zelfs als er uiteindelijk een polynoom voor y1 in termen van x1, x2 en x3 gemaakt is dan nog is het optimum van d[6(1-y1)/x3]/dx1 (en d[6(1-y1)/x3]/dx2 en d[6(1-y1)/x3]/dx3) niet zo snel gevonden, in ieder geval niet in formulevorm zoals de studenten hoopten want het nul stellen van de partiële afgeleiden leidt niet tot prettige vergelijkingen.
Mijn eigen conclusie: niet alle vraagstellers weten/kunnen wat hun vraag lijkt te suggereren.
Rare vragen IV: vier chemici op zoek naar een optimum (deel 1)
Op 1 september 2017 verscheen er een vraag op de wisfaq.nl die aanleiding bleek tot een hele serie reacties met vragen en wedervragen. Ik weet eigenlijk niet wie er meer geleerd heeft: de vraagstellers of ikzelf.
De vraag
Ik raad de lezer aan de vraag eerst zelf te lezen; dan zal duidelijk worden dat deze niet makkelijk is samen te vatten. Het probleem was namelijk, voor mij, dat de vraagstellers geen onderscheid leken te kunnen (of willen?) maken tussen enkel- en meervoud. Dat begon al met de zin “We beschikken over een uitgebreide reeksen.” En verder leek “y1 als functie van x1” eerst op één functie te slaan maar later op meer dan één: x2 ging voor variatie zorgen, en later kwam er ook nog een x3 in het spel. Enfin, mijn reactie laat zien dat men wel iets duidelijker kon zijn.
Eerste reactie
De eerste reactie probeerde een en ander te verduidelijken maar dat lukte niet echt; ik kon geen vinger achter de relaties tussen de, inmiddels zes, variabelen x1, x2, x3, y1, y2 en y3 krijgen. Ik maakte een minimaal datasetje dat, dacht ik, aan de eisen voldeed en vroeg hoe ze y1 als functie van x1 dachten te schrijven.
Tweede reactie
Geen reactie op de dataset maar nog meer uitleg van de werkwijze, zonder dat nu echt duidelijk wordt hoe y1 als functie van x1 te schrijven is. Nogmaals gevraagd hoe dat zou werken met het datasetje.
Derde reactie
Andermaal geen reactie op de dataset, wel de medeling “wij zijn studenten chemie, geen wiskunde”. De bijgeleverde uitleg van de vorm van de vier-dimensionale tabel bracht niet echt meer duidelijkheid. De mededeling aan het eind was van alles het meest zorgwekkend: studenten op een hogeschool zoeken wiskunde-experts op de wisfaq, niet op het eigen instituut. Ik heb ze aangeraden toch eens iemand op de eigen school aan te spreken.
Vierde reactie
Na een zo mogelijk nog cryptischere beschrijving van hun werkwijze komt de mededeling dat ze wel naar een docent zullen stappen.
Morgen meer.
Tijdrijden in Bergen
Deze week worden in Bergen, Noorwegen, de wereldkampioenschappen wielrennen op de weg gehouden, met vandaag, 20-09-2017, het tijdrijden voor de heren. Het parcours is interessant: een relatief vlakke rit met aan het eind een klim naar de top van Fløyen, een plek met een mooi uitzicht over de stad en de haven.
In de lokale krant Bergens Tidende staat het profiel van de rit getekent, met de laatste drie kilometer nog een keer apart in het onderstaande plaatje.
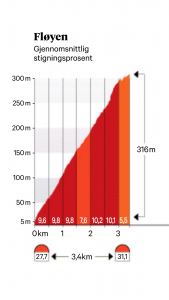
Dat ziet er dramatisch uit, tot je even naar de eenheden kijkt: horizontaal zijn dat kilometers, verticaal gaat het in stappen van 50 meter omhoog. En dat geeft, op zijn zachtst gezegd, een vertekend beeld. Ik heb, bij benadering, het echte profiel even geschetst.
![]()
Dat lijkt niet erg steil en zo van opzij ziet het er niet moeilijk uit; echter, bij wegen met een dergelijke helling staat vaak een waarschuwingsbord voor, juist, een steile helling. Een hellingspercentage van ongeveer 10 % betekent dat er constant met een kracht gelijk aan ongeveer 10 % van het gewicht van jezelf en je fiets tegen je aan geduwd wordt. Naar beneden is dat plezierig al zul je snel zien dat je in je remmen moet knijpen om niet te snel te gaan. Naar boven maak die kracht het fietsen al een stuk moeilijker.
Voor wie wil rekenen: denk maar eens aan de formule F=m×a (kracht is massa maal versnelling). De kracht recht naar beneden is gelijk aan g×m (hier is g de zwaartekrachtsversnelling, daar mochten we op school wel de waarde 10 voor nemen). Hiervan werkt 10 % langs de weg, dus onze F is gelijk aan g×m/10, van school mocht ik daar dus m van maken. Conclusie: de versnelling die we ondervinden als we freewheelend naar beneden gaan is 1 m/s2. Per seconde gaan we dus een meter per seconde sneller. Bereken zelf maar eens hoe snel je dat te link vindt worden.
Een meer dan reële kans?
Op twitter keek Marc van Oostendorp terug naar een blogpost van hemzelf over het woord `reëel’: Hoe reëel is meer dan reëel?. In dat stuk wordt gesproken van reële kansen en van kansen die meer dan reëel zijn. En toen sloeg mijn hoofd een beetje op hol: wat voor kansen zijn dat nou weer?
In de wiskunde wordt met het begrip `kans’ heel anders omgegaan dan in het dagelijks leven. In deze column van Ionica Smeets word de wiskundige opvatting van `kans nul’ vergeleken met de dagelijkse. In het kort: het wiskundige `kans nul’ betekent niet hetzelfde als `dat gebeurt niet’ maar als we horen dat de morgen de kans op regen nul is gaan we er van uit dat het morgen niet zal regenen.
Dat verschil brengt de professionele kansrekenaars er toe het woord `kans’ maar los te laten en het bijna-synonieme `waarschijnlijkheid’ gebruiken.
Maar goed, omdat die termen `kans’ en `waarschijnlijkheid’ buiten de wiskunde nagenoeg synoniem zijn kan men zich afvragen wat we aanmoeten met `reële kansen’ en `meer dan reële kansen’.
Wat het eerste betreft: `reële kansen’ is een pleonasme. De kans/waarschijnlijkheid van een gebeurtenis is, per definitie, een reëel getal uit het interval [0,1].
Maar nu het tweede, `meer dan reële kansen’. Wat moeten we daar als wiskundigen mee? Je zou kunnen denken een waarschijnlijkheden met waarden buiten de reële getallen. Is dat mogelijk? Zou je complexwaardige kansen kunnen hebben of zelf quaternion-waardige?
Als je naar de Axioma’s van Kolmogoroff kijkt lijkt het niet: de eerste eis is dat P(A)≥0 voor elke gebeurtenis. Aan de andere twee eisen is met complex- of quaternion-waardige kansen wel te voldoen; er is een goed ontwikkelde theorie van maten met waarden in de complexe getallen of in de quaternionen. Met een beetje goede wil kun je in dit geval een kansmaat definiëren als eentje die alleen waarden in de eenheidsbol aanneemt. De vraag is natuurlijk wat je je dan moet voorstellen bij negatieve of een zuiver imaginaire waarschijnlijkheid, maar we kunnen er in ieder geval mee rekenen. En, wie weet, het zou niet de eerste keer zijn dat zulk wiskundig speelgoed een toepassing vindt.
Er is nog een andere manier om kansen `meer dan reëel’ te maken en dat heeft, onder meer, te maken met die `kans nul’ van hierboven. Denk, bijvoorbeeld, aan de uniforme kansverdeling op het interval [0,1]. Deze kansverdeling beschrijft wat er gebeurt als je willekeurig pijltjes in dat interval gooit: de kans dat je het interval [⅓,⅔] raakt is gelijk aan ⅓ en in het algemeen: elk interval (a,b) heeft raakkans b-a. Het gevolg van deze afspraak is dat elk punt raakkans nul heeft. Echter, als je een pijltje in het interval gooit dan raak je een punt, ook al had je kans nul dat punt te raken. Dit is waar het in de column van Ionica Smeets om ging: wiskundig betekent `kans nul’ dus niet hetzelfde als `onmogelijk’.
Wat sommige mensen hierbij ook een beetje stoort is dat kansen niet altijd goed opgeteld kunnen worden: elk punt heeft raakkans nul en als we al die raakkansen optellen krijgen we weer nul, toch? Maar die som zou gelijk moeten zijn aan de kans dat je het interval [0,1] raakt en die is toch gelijk aan 1. Daarnaast is het ook nog zo dat niet elke deelverzameling van [0,1] een welgedefinieerde raakkans heeft. In de praktijk is dat allemaal niet zo erg: het gaat bij de berekeningen vrijwel nooit om individuele punten maar om verzamelingen, en die verzamelingen hebben hebben vaak beschrijvingen waaraan meteen te zien is dat ze een welbepaalde raakkans moeten hebben.
Wat te doen? Je kunt in het model van Solovay gaan werken; daar heeft elke verzameling een welgedefinieerde raakkans. Echter, de optelwet heb je daar nog steeds niet, en die kun je ook niet krijgen zolang je eist dat je raakkansen reële getallen zijn. En hier komen de meer dan reële kansen in beeld.
In dit artikel (ook hier te vinden) ontwikkelden Vieri Benci, Leon Horsten, en Sylvia Wenmackers een waarschijnlijkheidsrekening met waarden in het interval [0,1] van een veel grotere getallenverzameling dan R, maar die er wat elementaire algebra betreft niet van te onderscheiden is. Het onderscheid zit hem in de rijkheid van de verzameling en de mogelijkheid een heleboel oneindige sommen zinvol te kunnen behandelen. De raakkans van een enkel punt van het gewone interval [0,1] is positief maar kleiner dan elk `normaal’ positief reëel getal en dat maakt die kans `meer dan reëel’; ook de verzamelingen die geen welbepaalde raakkans hadden krijgen er nu een, maar ook die kansen zijn `meer dan reëel’.
Kwadratuur van de cirkel, II
Vorige keer hebben we bekeken wat `Kwadratuur van de Cirkel’ inhoudt in het kader van Euclidische Meetkunde. We hebben ook gezien dat kwadratuur van de cirkel niet mogelijk is met een passer en een latje. Deze keer gaan we bekijken of er andere manieren zijn om die kwadratuur uit te voeren.
Banach en Tarski
In het begin van de twintigste eeuw rees de behoefte om aan steeds meer deelverzamelingen van de getallenlijn, het vlak, en de ruimte respectievelijk een `lengte’, `oppervlakte’ of `volume’ toe te kennen. Om enige afstand tot de concrete meetkunde te bewaren begon men het woord `maat’ te gebruiken en de eerste die een goede definitie van `maat’ formuleerde was Lebesgue, in 1908.
Later is dit door anderen in zijn volle algemeenheid uitgewerkt maar in de bovengenoemde drie gevallen gebruiken we de Lebesgue-maat nog vrijwel zo als Lebesgue hem gedefinieerd heeft.
Voor bekende meetkundige figuren geeft de Lebesgue-maat de reeds bekende waarde maar voor willekeurige verzamelingen gaat het niet altijd even goed.
Een extreem voorbeeld hiervan werd gegeven door de Polen Banach en Tarski. Voortbouwend op werk van Hausdorff lieten ze zien dat men een massieve bol met straal 1 in eindig veel (vijf is genoeg) deelverzamelingen kan verdelen, en dat men daarna die eindig veel stukken in elkaar kan schuiven tot twee massieve bollen van straal 1. Wie met het artikel van Banch en Tarski in de hand nu een wonderbaarlijke vermenigvuldiging van één sinaasappel tot twee sinaasappels wil uitvoeren komt bedrogen uit.
De bollen zijn ideale wiskundige bollen, geen fysieke sinaasappels. En, en daar was het Banach en Tarski om te doen, de stukken waarin ze de bol verdeelden zijn zo lelijk dat er op geen enkele manier een maat aan toe te kennen is. Immers als dat wel mogelijk was dan zou 1+1=1 bewezen zijn.
Terug naar het vlak
De vraag is nu of de wonderbaarlijke vermenigvuldiging in het vlak ook mogelijk is. Dat bleek niet het geval. Als je een verzameling die een maat heeft in eindig veel deelverzamelingen verdeelt en als je die stukken, hoe lelijk ook, tot een andere verzameling in elkaar legt en die nieuwe verzameling heeft een maat dan zijn de maten van beide verzamelingen gelijk.
U voelt hem wellicht al aankomen: Tarski formuleerde een abstracte versie van `de kwadratuur van de cirkel’: kunnen we een cirkelschijf, zeg van oppervlakte 1, in eindig veel verzamelingen verdelen en die stukken weer in elkaar schuiven tot een vierkant van oppervlakte 1?
In 1990 beantwoordde Miklos Laczkovich deze vraag met “Ja”. De gebruikte stukken zijn vrij lelijk, maar ze hoeven alleen verschoven te worden, draaien hoeft niet. De kwadratuur van de cirkel is dus mogelijk, zij het met instrumenten die veel geavanceerder zijn dan een passer en een liniaal.
Iets over het woord `lelijk’. De ontdekkingen door Banach en Tarski en anderen van verzamelingen waaraan geen maat toe te kennen is leidden tot een vakgebied dat Beschrijvende Verzamelingenleer is gaan heten. Hierin worden verzamelingen geklassificeerd naar hun beschrijvingen; het `lelijk’ dat ik een paar keer gebruikt heb kan daar precies gemaakt worden: de verzamelingen van Banach en Tarski, en van Laczkowicz hebben, noodzakelijk, beschrijvingen die vele malen ingewikkelder zijn dan die van verzamelingen die je normaal tegenkomt als lijnen, krommen en andere herkenbare figuren.
En toch …
Aan het eind van 2016 kreeg dit verhaal nog een nieuw slot. Andrew Marks en Spencer Unger bewezen dat de kwadratuur van de cirkel met stukken gedaan kan worden die in de Beschrijvende Verzamelingenleer als zeer mooi zouden worden aangemerkt, de technische term is “van Borel-complexiteit ten hoogste vier”. Voor U naar de winkel holt om deze `heel mooie’ legpuzzel aan te schaffen: hoewel de stukken in het grote geheel van de deelverzamelingen van het vlak redelijk eenvoudig zijn, zijn ze nou ook weer niet zo makkelijk met de hand te maken en vast te pakken.
Daar komt nog bij dat er wel een heel grote doos nodig is om alle stukken in te bewaren: bij een lezing over dit resultaat werd Andrew Marks naar het aantal benodigde stukken gevraagd; zijn antwoord: in de orde van grootte van 10220. Dat is dus een Googol in het kwadraat, maal nog een keer 1020.
Verder lezen
Veel van wat hierboven is beschreven is uitgebreid na te lezen in The Banach-Tarski Paradox (second edition) van Grzegorz Tomkowicz en Stan Wagon uit 2016. Het resultaat van Marks en Unger is daar nog niet te vinden; `Borel circle-squaring’ is nog één van de grote open problemen in het boek. Wie zin heeft kan het artikel te pakken krijgen via arxiv.org.

Recent Comments