Posts in category rekenen
Hogere Machten
Gisteren bekeken we een weergave in woorden van een kansberekening in een column van Maarten Keulemans. Vandaag kijken we even naar die berekening zelf en hoe je snel iets over de 5000ste macht van een breuk als 9999/10000 kunt zeggen.
Even ter herinnering:
En het protest op De Dam? Misschien had men gewoon geluk, berekende epidemioloog Frits Rosendaal (LUMC). ‘De kans om corona te hebben, was op dat moment klein, ongeveer een op tienduizend’, stelt Rosendaal. ‘Dat maakt de kans dat van de 5.000 aanwezigen er een of meer besmettelijk waren, op dat moment 39 procent: 1 min 9.999 gedeeld door 10.000, tot de macht 5.000. Vandaar dat er niks gebeurd is.’
Gisteren hebben we gezien dat de te berekenen kans er zo uit moet zien:

Nu kun je die macht in een rekenmachientje stoppen en als dat goed geprogrammeerd is krijg je ongeveer 0,6065, en dat geeft inderdaad, afgerond, een kans van 39 procent.
Met de juiste formules kun je bijna uit het hoofd een goede onderschatting van de macht maken, en daarmee een overschatting van die kans. De eerste formule is een ongelijkheid:
![]()
Deze ongelijkheid heeft een naam: De Ongelijkheid van Bernoulli, deze geldt voor alle x-en groter dan -1 (en ongelijk aan 0), en alle nauurlijke getallen. Als we 9999/10000 schrijven als 1-1/10000 kunnen we x=-1/10000 nemen, en n=5000, met als resultaat

Zonder al te veel moeite zien we dat de kans in ieder geval kleiner dan ½ was. Voor dit soort schattingen is de Ongelijkheid van Bernoulli een mooi stuk gereedschap om bij de hand te hebben.
Wat scherper
Kan het beter? Ja natuurlijk. Wat extra kennis over over de rij (1-1/n)n vertelt ons dat

en daaruit vinden we dan (met een relatieve fout van niet meer dan 0,0001):

Hierin is e het grondtal van de natuurlijke logaritme.
Onze macht is dan ongeveer de wortel uit 1/e; en daar hebben we een reeks voor die iedere eerstejaars wiskundestudent leert:

En de eerste paar termen geven ons een antwoord dat al heel dicht bij het resultaat van het rekenmachientje ligt.
Binomium
Voor degenen die het Binomium van Newton kennen (en beheersen): schrijf de eerste paar termen van de uitgewerkte macht maar eens op en vergelijk met de som voor 1/√e.
Spreken met haakjes
In een column van Maarten Keulemans in de Volkskrant werd aan het eind even snel aangegeven hoe groot de kans was dat er bij de Black-Live-Matter demonstratie op 2 juni iemand was die met corona besmet was. Aan het eind gebeurde iets dat mij op het verkeerde been zette.
Daar stond namelijk dit
En het protest op De Dam? Misschien had men gewoon geluk, berekende epidemioloog Frits Rosendaal (LUMC). ‘De kans om corona te hebben, was op dat moment klein, ongeveer een op tienduizend’, stelt Rosendaal. ‘Dat maakt de kans dat van de 5.000 aanwezigen er een of meer besmettelijk waren, op dat moment 39 procent: 1 min 9.999 gedeeld door 10.000, tot de macht 5.000. Vandaar dat er niks gebeurd is.’
Ik heb de zinsnede waar ik over struikelde even rood gemaakt. Het gaat mij om die komma.
Voor de komma staat dus “1 min 9.999 gedeeld door 10.000” en na de komma “tot de macht 5.000”. Die komma had voor mij de functie van haakjes, en met Mijnheer Van Dalen aan mij zijde las ik het gedeelte ervoor als
![]()
en met de komma als haakjes las ik

en daar staat gewoon 0,00015.000 en dat is 10-20.000, veel kleiner dan 0,39 dus.
Dat was niet de bedoeling. De bedoeling was dat de haakjes heel anders stonden, namelijk zo:

Dat is nog lastig in zo’n snelle zin te formuleren; als ik dit op college zou doen zou ik het natuurlijk op het bord schrijven maar soms spreek ik het uit voor ik het opschrijf. Ik zou er dit van maken: “1 min de 5000ste macht van: 9999 gedeeld door 10000”. En bij die “9999 gedeeld door 10000” zou ik de haakjes met mijn armen uitbeelden.
Morgen zullen we even naar die 5000ste macht kijken: hoe kun je snel zien dat hij groter dan een half is? En dus die kans kleiner dan een half?
Het laatste cijfer
Op twitter werd gevraagd naar het laatste cijfer van het getal van Graham. Grappig genoeg heeft dat een redelijk eenvoudig antwoord.
In deze coronatijden krijgen ouders vragen van hun kinderen die deze meestal aan de onderwijzer(es) vragen, zoals
waarom eindigt dat op een 7, en niet op een 9 of een 0? Daar hield onze lokale kennis op, dus hopelijk weet jij raad @ionicasmeets ?
— Mirjam070 (@MvL070) April 5, 2020
Nu is het getal van Graham het resultaat van een ongelooflijk aantal malen machten van 3 nemen, in een toren van 3-en. Het resulterende getal is nog groter. Maar hoe zou je het laatste cijfer van dat getal kunnen bepalen? Dat is eenvoudiger dan het lijkt. We doen het in stappen.
Om te beginnen het getal is een macht van 3 en als we de eerste paar machten van 3 opschrijven, en alleen het laatste cijfer noteren vinden we 3, 9, 7, 1, 3, 9, 7, 1, … Dat dit zich zo blijft herhalen wordt duidelijk als je je realiseert dat het laatste cijfer van 3×n alleen van het laatste cijfer van n afhangt.
Welke van die vier cijfers is het nu? Welnu de exponent van het getal is weer een macht van drie en dus oneven. Dat betekent dat we alleen een 3 of een 7 als mogelijkheid overhouden. Als we van die exponent de rest kunnen vinden bij deling door 4 weten we welk van de twee het is.
Schrijf die resten maar op: 31 heeft rest 3; 32 heeft rest 1; 33 heeft rest 3; 34 heeft rest 1; … het patroon wordt duidelijk: bij oneven exponenten is het 1 en bij oneven exponenten is het 3.
Maar we hebben een toren van drieën, dus de exponent van de exponent is oneven en het eindcijfer is gelijk aan 7.
Iets geavanceerder
Als je hebt leren rekenen modulo getallen (`klokrekenen’) gaat het sneller.
Onze vondst van periode 4 vind je door te zeggen 31=3,
32=9, 33=27=7 modulo 10, 34=3×7=21=1 modulo 10 en zodra we 1 hebben gevonden is duidelijk dat we de periode hebben.
Dan moeten we modulo 4 rekenen om te weten of we 3 of 7 krijgen, maar 3=-1 modulo 4, dus 3k=(-1)k modulo 4 en dan is duidelijk wat we krijgen bij een oneven exponent.
Opgave
Probeer zelf de laatste twee cijfers van het getal van Graham te bepalen. Het duurt iets langer maar met een beetje volhouden kom je er wel.
KP checkt: Hartslag en de Gulden Snede
In deze blogpost beschreef ik een artikel waarin metingen aan mensenschedels moesten aantonen dat een aantal maten zich volgens de Gulden Snede zouden verhouden. De conclusies waren nogal discutabel maar ook al waren de getallen niet echt dicht bij de Gulden Snede ze leken tenminste te kloppen. In de referenties van het artikel vond ik veel verwijzingen naar andere voorkomens van de Gulden Snede. Twee daarvan heb ik nader bekeken: Golden Ratio is beating in our heart en Does systolic and diastolic blood pressure follow Golden Ratio. Daar kloppen de getallen iets minder goed.
Kloppende getallen
Wat bedoel ik met `kloppende getallen’? Welnu, als je een lengte, zeg A, in twee stukken verdeeld, zeg B en C, dan geldt natuurlijk A=B+C. Als je op jacht bent naar de Gulden Snede neem je de grootste van de twee stukken, zeg C, en dan bekijk je de verhoudingen A/C en C/B. Je hoopt dat die verhoudingen gelijk zijn want dan heb je de Gulden Snede te pakken.
Tussen die twee verhoudingen bestaat een relatie: deel de gelijkheid maar door C dan krijg je A/C=B/C+1, of iets ingewikkelder opgeschreven: A/C=1/(C/B)+1. Als we onze twee verhoudingen even afkorten, A/C=y en C/B=x, dan staat hier y=1/x+1.
Anders gezegd: het punt met coordinaten (C/B,A/C) ligt op de grafiek van y=1/x+1.
In het artikel Mammalian Skull Dimensions and the Golden Ratio worden de volgende gemiddelden van de verhoudingen gerapporteerd: A/C=1.64 ± 0.04) en C/B=1.57 ± 0.10 (de letters zijn anders, maar het gaat om de getallen).
Niet alleen het punt (1.57,1.64) ligt op de grafiek van y=1/x+1 maar ook de punten (1.47,1.68) en (1.67,1.60); deze worden bepaald door de randpunten van de intervallen (1.60,1.68) (voor A/C) en (1.47,1.67) (voor (C/B). Zie het plaatje hieronder.
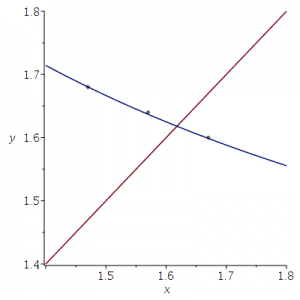
Dit bedoel ik met kloppende getallen: de resultaten horen in ieder geval bij de stituatie waar A=B+C.
Overigens laat ik het aan de lezer om te beoordelen, gezien dit plaatje, in hoeverre deze conclusie gerechtvaardigd is:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Het snijpunt van de twee grafieken (y=1/x+1 en y=x) is het punt (Φ,Φ), en daar ligt (1.57,1.64) toch nog wel ver vandaan.
Hartslag en bloeddruk
In de referenties van het schedelartikel vond ik de artikelen die hierboven genoemd werden.
Hartslag
Om te beginnen: in Golden Ratio is beating in our heart wordt de Gulden Snede ontdekt in verhoudingen van tijdsintervallen in de hartslag. Een mooi plaatje met een uitleg van alle termen staat op de wikipedia-pagina over het QRS-complex:

De drie grootheden waar het hier om gaat zijn: (A) het R-R-interval (tussen twee opeenvolgende R-en), (B) de systole (samentrekfase), en (C) de diastole (ontspanningfase).
De letters komen overeen met onze eerste paragraaf en met de verhoudingen waar het artikel over gaat.
De resultaten zijn
- A=866 ± 73
- B=333 ± 22
- C=536 ± 66
- C/B=1.611
- A/C=1.618
Deze getallen zijn problematisch.
Ten eerste tellen de gemiddelde waarden niet goed op: A=866 en B+C=869. Dat zou wel moeten als alle metingen goed waren dan geldt A=B+C voor elke meting en dan ook voor de gemiddelden.
Ten tweede: als een van de verhoudingen gelijk is aan Φ dan is de andere dat ook, hier is dat niet zo.
Ten derde: als je, net als in het schedelmetingartikel, de verhoudingen van de gemiddelden neemt kom je op andere getallen uit: 866/536=1.61567 en 536/333=1.6096.
Het zou kunnen zijn dat de gerapporteerde verhoudingen gemiddelden zijn van de verhoudingen per meting maar dan hadden de auteurs dat wel even mogen vermelden.
Voorlopig geloof ik niets van de conclusies van het artikel.
Het lijkt er op dat de individuele verhoudingen wel zijn uitgerekend want het artikel bevat nog een niet-ter-zake-doende grafiek waarin de verhouding C/B is uitgezet tegen de hartslag.

Daar is in ieder geval te zien dat de verhouding C/B behoorlijk variabel is.
Bloeddruk
In het artikel Does systolic and diastolic blood pressure follow Golden Ratio gaat het om de bloeddruk. De grootheden zijn nu: (A) de systolische druk (bovendruk), (C) de diastolische druk (onderdruk), en (B) hun verschil; alle in mm Hg.
| A | C | B | A/C=y | C/B=x | |
|---|---|---|---|---|---|
| etmaal | 137 ± 16 | 86 ± 12 | 51 | 1.59 | 1.69 |
| dag | 140 ± 17 | 89 ± 12 | 51 | 1.57 | 1.75 |
| nacht | 131 ± 18 | 80 ± 13 | 51 | 1.64 | 1.62 |
Wat hier opvalt is dat er voor het verschil geen interval is opgegeven; alsof het bij alle metingen precies 51 mm Hg was (dat geloof ik dus niet). De verhoudingen komen hier wel voort uit de gemiddelden behalve de verhouding C/B in de nacht: 80/51=1.56862. Laat die foute 1.62 nou net de verhouding zijn die het dichtst bij de Gulden Snede ligt.
Ik heb de punten vergeleken met de grafiek van y=1/x+1.
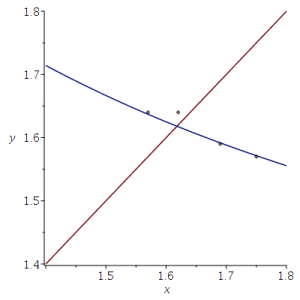
De twee punten rechts horen bij de verhoudingen voor een etmaal en overdag. Het meest linkse punt hoort bij de echte nachtelijke verhoudingen. Het punt dat ruim boven de grafiek ligt hoort bij de gerapporteerde nachtelijke verhoudingen. Ik heb geen idee hoe dat gebeurd kan zijn.
De koningin en de profeet
Via facebook kwam ik bij dit artikel uit The Poke: de Koningin van Engeland zou afstammen van de profeet Mohammed. Het refereert aan een stuk uit de Daily Mail van vorig jaar. Maar goed, is dit bijzonder?
Een nuttig gegeven in het artikel is dat we van de koningin 43 generaties terug moeten om bij de profeet te komen. Daar kunnen we mee rekenen.
Op deze pagina wordt met veel slagen om de arm geschat hoeveel mensen er ooit op aarde geleefd hebben. Dat zouden er zo’n 108 miljard zijn. Op die pagina staat een tabel met bevolkingsaaantallen voor diverse jaartallen. Daaruit kunnen we schatten dat er in de tijd van Mohammed niet veel meer dan 400.000.000 mensen op de hele aarde leefden.
Aan de andere kant: als we vanuit om het even welk persoon 43 generaties terug in de tijd gaan en consequent bij elke voorouder de naam van de vader en moeder op zouden schrijven, dan bevat elke nieuwe generatie twee keer zoveel namen als de voorgaande: twee ouders, vier grootouders, acht overgrootouders, enzovoort. De 43ste generatie bevat dan 243=8.796.093.022.208 namen.
Wat dan overduidelijk is dat er heel wat personen meer dan één keer in die 43ste generatie genoemd zullen worden: gemiddeld ruim 20.000 maal. Als je zo naar die getallen kijkt wordt het hoogst onwaarschijnlijk dat Mohammed niet een voorouder van de koningin is.
Er zijn natuurlijk geografische omstandigheden die personen uit bepaalde gebieden wat onwaarschijnlijker als voorouder maken, maar er is altijd veel verkeer tussen Europa en de Arabische wereld geweest. Ik hou het er op dat het helemaal niet bijzonder is dat er een lijntje loopt van Mohammed naar Elizabeth. Het zou wel knap zijn als ze echt zo’n lijntje zouden hebben gevonden.
Exacte oplossingen
Een veel voorkomende vraag op de wisfaq is: “Hoe los ik … op?” Op de plaats van de puntjes staat dan een vergelijking die maar niet tot een mooie oplossing wil leiden, zoals bijvoorbeeld -x2+4x-3 = sin(x). Het antwoord op de vraag is vaak: “Het kan niet exact, doe maar een numerieke benadering.” Maar wat betekent `exact’ eigenlijk?
Heel veel wiskundesommen komen uiteindelijk neer op het oplossen van een vergelijking, het invullen van een of meer getallen in een of andere uitdrukking, en/of het daarna vereenvoudigen van de uitkomst tot …, tot wat eigenlijk? Tot een compacte overzichtelijke uitdrukking waarvan wellicht ook makkelijk te controleren of het een oplossing van het probleem is. Wat een compacte overzichtelijke uitdrukking is varieert met de tijd. Het begint met natuurlijke getallen; een antwoord als `3′ is duidelijk en je kunt waarschijnlijk natellen of het klopt. Vrij snel komen (positieve) breuken bij het verdelen van dingen (traditioneel taarten) over personen: drie taarten over vijf personen eerlijk verdelen levert iedereen 3/5 taart op. Nog later komen er negatieve getallen bij, meestal uitgelegd als `schuld’.
Dat is allemaal nog redelijk overzichtelijk maar dan wordt het spannender: als je een vierkant met een oppervlakte van 2 m2 wilt maken dan heb je niks aan al die breuken, positief of niet. Om praktische redenen is het wel gewenst de lengte van de zijden van dat vierkant te benoemen, en dat heeft geleid tot een van de eerste afkortingen die je bij de wiskunde leert: √2. Dat getal is echt nieuw, niet te weer te geven als een breuk. Er is zelfs een heel Zebraboekje aan √2 gewijd.
Het interessante is dat na verloop van tijd dat symbool √ heel vertrouwd wordt en dat we het accepteren als ingredient in die `compacte overzichtelijke’ uitdrukkingen. Met de abc-formule als eerste hoogtepunt. Ondanks het feit dat √D niet meer is dan een afkorting van “het positieve reële getal waarvan het kwadraat gelijk is aan D”.
Een andere bekende afkorting is natuurlijk π: de verhouding tussen omtrek en diameter van een cirkel. Ook π is niet als breuk uit te drukken, erger nog: met π is algebraïsch helemaal geen goed garen te spinnen. Maar π komt in zoveel uitkomsten en formules voor dat het onderhand een vertrouwde vriend geworden is.
Op de middelbare school en later stijgt het aantal `vertrouwde vrienden’ snel, via allerlei nieuwe functies als sinus, cosinus, e-macht, logaritme, … Zo is de lengte van het stukje van de parabool met vergelijking y=x2 tussen de punten (0,0) en (1,1) gelijk aan
![]()
en niemand knippert met de ogen. Als je de echte betekenis van die uitdrukking wilt achterhalen zul je vrij diep de wiskunde in moeten duiken want hij hangt van afkortingen aan elkaar.
Even terug naar de vergelijking aan het begin. Heeft die vergelijking wel oplossingen? Ja, daar kun je je van overtuigen door de grafieken van het linker- en rechterlid even te schetsen; je ziet dan dat er een intervalletje is waarop -x2+4x-3 groter is dan sin(x) en de eindpunten van dat intervalletje zijn de oplossingen van de vergelijking. Is er een formule voor de linkeroplossing? Ja:
![]()
deze komt direct uit het bewijs van de tussenwaardestelling. Die stelling zegt dat dat minimum bestaat, noem het even a, en dat a daadwerkelijk aan de vergelijking voldoet. Voor wie dit geen mooie formule vindt, bedenk dan dat √2 niets meer is dan een afkorting voor
![]()
hetwelk volgens diezelfde tussenwaardestelling bestaat.
Met a en √2 is goed te werken; je kunt ze in allerlei uitdrukkingen stoppen en die weer proberen te vereenvoudigen. In het geval van √2 vervang je telkens (√2)2 door 2; probeer maar eens aan te tonen dat
![]()
Wat a betreft: telkens als je sin(a) ziet kun je daar -a2+4a-3 van maken (of omgekeerd); dat gebeurt niet zo vaak en daarom zal a lang niet zo vertrouwd worden als √2 dat al eeuwen is.
En tau rund jorden, II
Dette er andre delen av en oversettelse av en artikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger). Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen? Kan vi uttrykke høyden i lengden vi spleiset inn?
I går vi så at når vi tar en tau som er en meter langre enn jordens omtrekk og drar tauen strammt ved Nordpolen så skal det høyeste punktet være på 121 meter og lit mer. I dag skal vi lage en enkel formel med radiusen og ekstra lengden i som gir en god approksimasjon av høyden.
En effektiv approksimasjon
Her er tegningen fra i går igjen
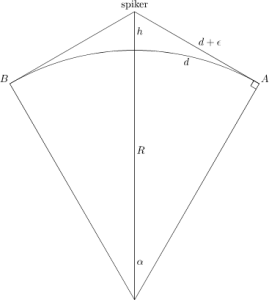
Fra Pythagoras sin læresetning lærte vi at
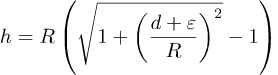
Fra bildet ser vi også at
![]()
Dette kan kombineres til denne ligningen
![]()
Nå har vi et uttrykk for h som bruker R og α men vi trenger et som bruker ε. Dette må gjøres implisitt fordi α er en løsning av
![]()
og der er ingen `pen’ (eller stygg) formel for løsningene.
Som vi så i går er vinkelen α veldi liten (0.006176 radianer). Nå er det slik at α+α3/3 er en veldi bra approksimasjon av tanα. Hvis vi setter dette uttrykket i ligningen så får vi
![]()
Også tanα er veldi liten.
Og for x nær 0 har vi √(1+x)≈1+½x; nå kan vi forenkle formelen for h til en approksimasjon
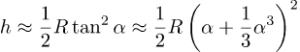
Neste steg er å skrive ut kvadraten
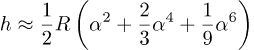
Når vi setter i tallene så får vi Rα2=242.8 m, Rα4=0.009 m og Rα6=3.5×10-7 m. Vi derfor kan trygt kaste fjerde og sjette potensene og så får vi denne approksimasjonen for h:
![]()
Lit lengre siden fant vi at
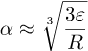
Vi setter det inn i approksimasjonen og får
![]()
Nå bruker vi verdien av R og får til slutt
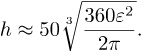
Det flotte med denne formelen er at den gir nesten samme svaret som i går: setter vi inn ε=0.5 så får vi h≈121.4 m igjen.
Oppgav
Sett inn ε=0.005 in formelen vår. Hvor mye forskjeller resultatet fra verdien av h som vi fikk i går?
Exercise
Undersøk hvor bra approksimasjonen √(1+x)≈1+½x er. For eksempel, sammenlign (1+½x)2 med 1+x; for hvilken x er forskjellen liten nok til å bli kastet? Er du enig i hvordan approksimasjonen brukes her?
Bemerkning
Vi kan isolere ε i formelen:
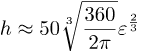
dette gir viktig kvalitativ informasjon: h er omtrent lik en konstant ganger ε2/3.
Hvis du er kjent med Taylorpolynomer kann det være gøy å finne ut hvor stor feilen er (hvilken potens av ε) i denne approksimasjonen.
En tau rund jorden, I
Dette er første delen av en oversettelse av en art ikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger).
Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen?
Fast alle har hørt om følgende oppgaven. Vi tar en tau og strekker den rund jorden, langs polene, slik at den sitter tett. På Nordpolen spleiser vi inn en ekstra meter tau. Så drar vi, og mange folk rund jorden, tauen opp slik at den er overalt like høyt over jordoverflaten; den blir en sirkel igjen. Hvor høyt kommer den til å bli? Kan en mus komme seg under tauen?
Svaret, tauen skal være overalt 16 centimeter høyt, blir en overraskelse for mange folk. inntil du utfører beregningen. Vi begynner med en tau som er 2πR lang, der R er jordens radius. Oppgaven er å bestemme radiusen til sirkelen som er en meter lengre. Det vil si: bestem R’ slik at 2πR’=2πR+1. Men det er lett å gjøre: divider med 2π, så får vi R’=R+1/(2π)≈R+0.159.
Beregninger viser at verdien av R er ikke viktig: hvis du forlenger en sirkel med en meter så forlenger du radiusen med nesten 16 centimeter.
Vi henger jorden på en spiker
Men hva om vi drar opp tauen bare på Nordpolen til den er helt stramm igjen? Som om vi skule bruke tauen til å henge jorden på en spiker. Hvor høyt kommer spikeren til å bli over Nordpolen? Kan en isbjørn komme seg under tauen?
Her er en tegning som viser hva vi prøver å gjøre.

Det er lit enklere med bokstaver: R er jordens radius, ε er halvparten av tauen vi spleiset inn (en halv meter altså) og h er svaret på spørsmålet.
Buen d viser distansen fra Nordpolen til begge punktene der tauen sist berører jorden.
Vi har en rett vinkel i A (og B) fordi linjen fra A til spikeren er en
tangent til sirkelen. Nå kan vi finne en formel for h.
Vi begynner med Pythagoras sin læresetning:
![]()
og så h+R=±√(R2+(d+ε)2), eller
![]()
Dersom h er positiv må vi ta plussen, og
![]()
Vi tar R utenfor parentesen og får
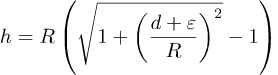
Det vi ikke vet her er verdien til d. Vi bruker radianer, og derfor d=αR eller α=d/R fordi, som vi skal se, det er enklere å lage en ligning for α.
Fra bildet ser vi hva tangensen til vinkelen α er:
![]()
og derfor
![]()
eller
![]()
Så, vår α er en løsning på siste ligningen.
Nå trenger vi noen tall. Jordens omkrets er, per definisjon, 40.000 km
(se illustrasjonen her). Derfor R=40.000.000/(2π) m og, selffølgelig, ε=½ m. Det betyr at vi må løse
![]()
Det finnes ingen enkelt formel for løsningen; det beste vi gjøre er å løse ligningen numerisk. De fleste grafiske kalkulatorene kan gjøre det for deg og jeg fikk denne løsningen: alpha;≈0.006176=6.176×10-3 og det betyr at d≈247.040 km. Det er interessant å vite hvor langt fra Nordpolen tauen forlater jorden men vi trenger ikke d i beregningene våre: vi setter α for d/R in formelen for h:
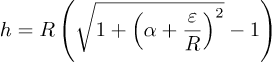
Når vi taster alle tallene in kalkulatoren får vi h≈121.4 m.
Oppgave
Gjør alt igjen men nå spleiser du inn bare en centimeter tau. Hvis tauen er lett nok kan du dra den stramm uten hjelp?
Selv om vi ikke har en eksakt formel for h som involverer ε og R kan vi noe om relasjonen mellom de tre størrelsene. Jeg skal skrive noe om det senere, in andere delen av denne historien.
Bruggen bouwen
In het Noorse radioprogramma Abels Tårn werd op 23 maart een poging gedaan uit te leggen waarom Robert Langlands de Abelprijs 2018 had gekregen. “Hij bouwde bruggen tussen diverse gebieden in de Wiskunde.” Veel verder ging de discussie niet; al viel de kreet `Automorfe Vormen’ nog even.
Voor wie wil weten wat het Langlands Program inhoudt kan op op de website van de Abelprijs wat inleidende artikelen vinden. In het radioprogramma werd nog even verwezen naar een eerdere winnaar Andrew Wiles. Diens bewijs van de Grote Stelling van Fermat is een voorbeeld van het gebruik van zo’n brug tussen Getaltheorie aan de ene oever en Algebraïsche Meetkunde aan de andere.
Ik vroeg me af of er niet een klein bruggetje tussen getaltheorie en meetkunde (algebraïsch of anderszins) bestaat dat als illustratie kan dienen.
Misschien helpt dit, een eenvoudige getaltheoretische vraag: bestaan er twee kwadraten (van natuurlijke getallen) waarvan de ene het dubbele van de andere is? Dat wil zeggen: zijn er twee natuurlijke getallen, m en n, zo dat n2=2×m2?
Je kunt voor dit probleem een brug naar de meetkunde slaan: teken twee vierkanten, een van n bij n en een van m bij m. De vraag is of je m en n zo kunt kiezen dat de oppervlakte van het eerste vierkant twee keer zo groot is als het tweede.
In de meetkundige versie kun je de vierkanten als hieronder tekenen.
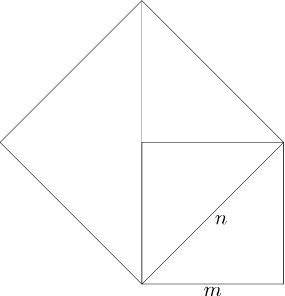
Om een gegeven vierkant in oppervlakte te verdubbelen moet je een vierkant tekenen waarvan de zijden gelijk zijn aan de diagonaal van het eerste vierkant.
Neem nu de rechthoekige driehoek met zijden m, m en n. Pas m af op de schuine zijde en teken de lijn vanuit z loodrecht op de schuine zijde naar de basis.
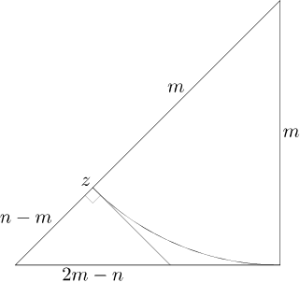
De schuine zijde van de nieuwe driehoek is de diagonaal van een vierkant met zijden n-m en dus geldt dat het kwadraat van die zijde gelijk is aan 2(n-m)2. Schrijf dat uit en gebruik dat n2=2m2:
2(n-m)2=2n2-4nm+2m2=4m2-4nm+n2=(2m-n)2
Dus die schuine zijde is inderdaad 2m-n lang.
Dit laat zien dat het niet mogelijk is natuurlijke getallen m en n te vinden als gewenst: als er twee van die getallen zijn dan kun je twee andere vinden die kleiner zijn. Maar in de natuurlijke getallen geldt: als er een getal met een bepaalde eigenschap bestaat dan is er ook een kleinste getal met die eigenschap. We hadden dus onze m en n zó kunnen kiezen dat n het kleinste getal is waarvoor een m bestaat met n2=2m2 en dan is 2m-n een echt kleiner getal met dezelfde eigenschap. Die tegenspraak laat zien dat zo’n n er in het geheel niet is.
Dus, als in het bewijs van Wiles, heeft de meetkunde geholpen bij het oplossen van een getaltheoretisch probleem.
Overigens heeft het getaltheoretische probleem een eenvoudige getaltheoretische oplossing: in een kwadraat n2 komt de priemfactor 2 een even aantal malen voor, namelijk twee keer zo vaak als in n zelf. En in het dubbele van een kwadraat, 2m2 komt 2 een oneven aantal malen voor: een even aantal maal in m2 plus de ene extra factor 2. Dus 2m2
is nooit gelijk aan n2.
En vele mensen hopen dat de grote stelling van Fermat ook zo’n eenvoudig bewijs heeft.
KP checkt: 200 liter inkt
Op twitter toonde Dap Hartmann zich een aanhanger van regel 17 uit The Elements of Style: Omit needless words (er zijn twee regels 17, dit is de eerste). Dat zou hem bij het nakijken wel 200 liter (rode?) inkt per jaar besparen.
Navraag leerde dat Dap met een vulpen nakijkt. Een snelle zoektocht leerde dat vulpeninkt in potjes van, onder meer, 60 en 80 ml wordt verkocht. Nu rekent 80 ml iets makkelijker: er gaan 12.5 van die potjes in een liter, en dus 2500 potjes in 200 liter.
Als Dap 50 weken per jaar van maandag tot en met vrijdag zit na te kijken (welk een plichtsbetrachting) dan komen die 200 liter neer op 10 potjes inkt per dag.
Ik denk dat Dap van de stijlfiguur `overdrijving’ gebruik heeft gemaakt.

Recent Comments