En tau rund jorden, I

Dette er første delen av en oversettelse av en art ikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger).
Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.

Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen?

Fast alle har hørt om følgende oppgaven. Vi tar en tau og strekker den rund jorden, langs polene, slik at den sitter tett. På Nordpolen spleiser vi inn en ekstra meter tau. Så drar vi, og mange folk rund jorden, tauen opp slik at den er overalt like høyt over jordoverflaten; den blir en sirkel igjen. Hvor høyt kommer den til å bli? Kan en mus komme seg under tauen?

Svaret, tauen skal være overalt 16 centimeter høyt, blir en overraskelse for mange folk. inntil du utfører beregningen. Vi begynner med en tau som er 2πR lang, der R er jordens radius. Oppgaven er å bestemme radiusen til sirkelen som er en meter lengre. Det vil si: bestem R’ slik at 2πR’=2πR+1. Men det er lett å gjøre: divider med 2π, så får vi R’=R+1/(2π)≈R+0.159.

Beregninger viser at verdien av R er ikke viktig: hvis du forlenger en sirkel med en meter så forlenger du radiusen med nesten 16 centimeter.

Vi henger jorden på en spiker

Men hva om vi drar opp tauen bare på Nordpolen til den er helt stramm igjen? Som om vi skule bruke tauen til å henge jorden på en spiker. Hvor høyt kommer spikeren til å bli over Nordpolen? Kan en isbjørn komme seg under tauen?

Her er en tegning som viser hva vi prøver å gjøre.

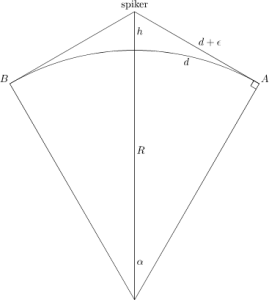
Det er lit enklere med bokstaver: R er jordens radius, ε er halvparten av tauen vi spleiset inn (en halv meter altså) og h er svaret på spørsmålet.
Buen d viser distansen fra Nordpolen til begge punktene der tauen sist berører jorden.
Vi har en rett vinkel i A (og B) fordi linjen fra A til spikeren er en
tangent til sirkelen. Nå kan vi finne en formel for h.

Vi begynner med Pythagoras sin læresetning:

og så h+R=±√(R²+(d+ε)²), eller

Dersom h er positiv må vi ta plussen, og

Vi tar R utenfor parentesen og får

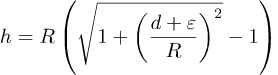
Det vi ikke vet her er verdien til d. Vi bruker radianer, og derfor d=αR eller α=d/R fordi, som vi skal se, det er enklere å lage en ligning for α.

Fra bildet ser vi hva tangensen til vinkelen α er:

og derfor

eller

Så, vår α er en løsning på siste ligningen.

Nå trenger vi noen tall. Jordens omkrets er, per definisjon, 40.000 km
(se illustrasjonen her). Derfor R=40.000.000/(2π) m og, selffølgelig, ε=½ m. Det betyr at vi må løse

Det finnes ingen enkelt formel for løsningen; det beste vi gjøre er å løse ligningen numerisk. De fleste grafiske kalkulatorene kan gjøre det for deg og jeg fikk denne løsningen: alpha;≈0.006176=6.176×10^-3 og det betyr at d≈247.040 km. Det er interessant å vite hvor langt fra Nordpolen tauen forlater jorden men vi trenger ikke d i beregningene våre: vi setter α for d/R in formelen for h:

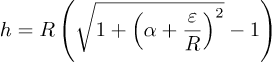
Når vi taster alle tallene in kalkulatoren får vi h≈121.4 m.

Oppgave
Gjør alt igjen men nå spleiser du inn bare en centimeter tau. Hvis tauen er lett nok kan du dra den stramm uten hjelp?

Selv om vi ikke har en eksakt formel for h som involverer ε og R kan vi noe om relasjonen mellom de tre størrelsene. Jeg skal skrive noe om det senere, in andere delen av denne historien.

Be Sociable, Share!

• 
•