Posts in category rekenen
Fruitmanden samenstellen
Op Facebook stond in de groep Wiskundelessen de volgende vraag (verkort weergegeven): “Hoeveel fruitmanden met zes stuks fruit kun je samenstellen uit vier kiwis, vijf bananen, zes peren, en zeven appels?” De vraagsteller wist dat het antwoord 79 moest zijn maar zag geen manier om daar aan te komen.
Een reageerder vond 79 wel erg weinig want het aantal manieren om 6 dingen uit 22 te kiezen, zonder op de volgorde te letten, is gelijk aan de binomiaalcoëfficiënt 22 boven 6 en die is gelijk aan 74613.
Dat antwoord zou kloppen als de vruchten er wel erg verschillend uit zouden zien. De vraagstelling vermeldt dat niet en het antwoord 79 suggereert dat de vruchten van dezelfde soort ononderscheidbaar zijn.
Hoe pak je zoiets aan? Elke fruitmand is eigenlijk een woord van zes letters, gekozen uit {k,b,p,a}, en gesorteerd: eerst de k’s, dan de b’s, de p’s, en aan het eind de a’s . Bijvoorbeeld kkbbpa, aaaaaa, ppppp, … Die woorden kun je lezen als producten: k2b2pa, a6, p6, … Het komt er dus op neer al dat soort producten te tellen. Hoe doe je dat systematisch, zonder een product te missen?
Dat gaat het best met wat eenvoudige algebra, werk het volgende product uit:
(1+k+k2+k3+k4)(1+b+b2+b3+b4+b5)(1+p+p2+p3+p4+p5+p6)(1+a+a2+a3+a4+a5+a6+a7)
Je krijgt dan alle mogelijke gesorteerde woorden met ten hoogste vier k’s, vijf b’s, zes p’s en zeven a’s.
Nu nog even de woorden van zes letters opzij zetten en tellen: klaar.
Dat kan nog iets sneller: maak van elke letter een x. Elk woord van zes letters wordt dan x6 en dat maakt het uitwerken van het product wat makkelijker.
(1+x+x2+x3+x4)(1+x+x2+x3+x4+x5)(1+x+x2+x3+x4+x5+x6)(1+x+x2+x3+x4+x5+x6+x7)
Met (be)hulp van Maple is het resultaat snel gevonden:
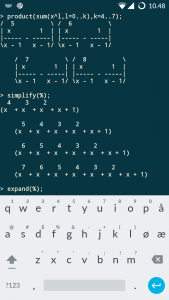

Inderdaad: 79 fruitmanden met zes vruchten. We kunnen nu ook aflezen hoeveel fruitmanden met andere aantallen vruchten gemaakt kunnen worden.
In het februarinummer uit 2016 van Pythagoras staat nog meer over deze manier van combinaties tellen.
Nul tot de macht nul
In de Facebookgroep Leraar Wiskunde ontspon zich een discussie over de waarde van 00 (nul tot de macht nul). Het begon met een opinieonderzoek met als opties
- 0
- 1
- onbepaald
De macht 00 komt wel eens voor bij het bepalen van limieten: als f(x) en g(x) limiet 0 hebben (als x naar een reëel getal of ∞ gaat) wat is dan de limiet van f(x)g(x)?
Je kunt proberen 00 te definiëren maar dat zal altijd een beetje onbevredigend blijven.
Het uitgangspunt zal natuurlijk de situatie zijn waar xy undubbelzinnig afgesproken kan worden. Dat is voor positieve x. Voor rationale y komt men met interpretatie `herhaald vermenigvuldigen’ een heel eind, zie bijvoorbeeld dit artikel in Pythagoras; daar wordt ook uitgelegd wat te doen als y irrationaal is.
Een andere aanpak is die van Cauchy. In zijn Analyse Algébrique vindt men vanaf bladzijde 106 hoe de continue functies φ te bepalen die voldoet aan de vergelijking φ(x+y) = φ(x)×φ(y). Het resultaat: exponentiële functies: er geldt φ(x)=φ(1)x.
Niets weerhoudt ons ervan te kijken wat er gebeurt als we φ(1)=0 eisen. Dan kunnen we het bewijs volgen zolang de exponent positief is; het resultaat is dat noodzakelijk 0x=0 en continuïteit dwingt ons dan 00=0 te nemen.
Aan de andere kant: Cauchy concludeerde ook dat φ(0)=1 in alle gevallen dat φ(1)>0; dan leidt een limietovergang tot de conclusie 00=1.
Er zijn natuurlijk diverse andere manieren om 00 via een limiet aan te pakken: voor de hand ligt te kijken wat met xx gebeurt als x (van boven) naar 0 nadert. Dat gaat het snelst via de gelijkheid xx=ex×ln(x): de limiet van die exponent is gelijk aan 0, dus de gehele limiet is gelijk aan 1.
Ik zou zeggen dat mogelijkheid 3 toch wel de juiste is.
Dat kunnen we nog beter beargumenteren door wat meer functies in het probleem van de limiet van de macht f(x)g(x) te stoppen.
Neem eens f(x)=exp(-1/x) en g(x)=x; beide functies hebben limiet 0 als x (van boven) naar 0 gaat. Maar f(x)g(x) is constant, met waarde e. Een kleine variatie: neem a>0 en verander g(x) in a×x; dan is de limiet gelijk aan e-a. We kunnen dus elk positief getal als limiet krijgen.
En het volgende paar functies geeft aan dat ∞ ook mogelijk is: neem f(x)=exp(-1/x^2) en g(x)=-x, dan is f(x)g(x) gelijk aan exp(1/x), met limiet ∞ als x (van boven) naar 0 gaat.
Misplacing ones excrement
In the somewhat more colourful language of this site: The Internet is losing its shit over this second grade math problem.
What is the problem?
“There are 49 dogs signed up to compete in the dog show. There are 36 more small dogs than large dogs signed up to compete. How many small dogs are signed up to compete?”
The answers that are discussed on the site are
- 36, with an argument not worthy of the name: 49-36=13, so 13 large dogs, so the answer is 36
- 42.5, because 49-36=13, 13/2=6.5 and 36+6.5=42.5
- 36 once more, but with the added information that 36-13=23, that’s 23 more small dogs
Answers 1 and 3 suffer from something that I observe with many first-year students: I ask something, in a Calculus class it is quite often a primitive function, and many suggestions come flying in, with the expectation that I will deem one of them correct. My reaction then is: you could have checked your answer yourself, in the case of the primitive by differentiation. That is why I asked that question in the first place: to show that they can verify many of their solutions by just substituting back into whatever it was they were solving.
You can verify whether 36 is correct: 36 small dogs is 23 more than 13 large dogs and 23 is definitely not equal to 36. So, no, 36 is not the correct answer.
The second answer — “That’s how I did it in my head.” — is correct, albeit unfortunate for one dog. It is also how I would (try to) explain it to a second-grader.
There are 36 more small dogs than large dogs, so we can set 36 small dogs aside and then look at the remaining dogs. If we want to keep the difference equal to 36 then we must be able to take away two dogs at a time (small and large) from those remaining until we have a group of small and a group of large dogs left. Most likely the second-grader will tell you that that is not going to happen with an odd number of dogs. The conclusion of course is that this is an ill-posed problem.
You can solve this problem — or rather, show it’s unsolvability — in other ways.
The sum of the two numbers in question is odd, that means that they have different parity, i.e., one is odd the and other is even, but then their difference is odd as well and it can’t be 36.
Or you can introduce letters, S and L, and express the demands as equations: S+L=49 and S-L=36. Solving these will lead to the solution done in the head: 2S=85, hence S=42.5 and L=6.5.
I hope that the teacher will admit that there was an error in the problem and that they will turn this into a valuable lesson: you can often check whether your answer is correct or makes sense.
Flauwekul
Op de Facebookpagina Wiskundelessen stond laatst een oude bekende: een bewijs van de gelijkheid 2=1 door middel van differentiëren. Dat gaat als volgt: schrijf x2=x×x=x+x+…+x (met x termen). Links en rechts differentiëren geeft 2x=1+1+…+1 (met x termen) en dus 2x=x en daarmee 2=1.
De commentaren vielen eigenlijk een beetje tegen. De enig juiste reactie zou moeten zijn: dat is flauwekul.
Hoezo flauwekul? Nou, vul voor x maar eens iets in als π of ½. Zie je het voor je? Je neemt een halve term die gelijk is aan ½ en die tel je op ….
Hier zit een serieus probleem achter: in het basisonderwijs komt vermenigvuldiging vaak eerst te voorschijn als afkorting voor herhaald optellen van hetzelfde getal. Immers, 5×6 is toch wat korter dan 6+6+6+6+6. Later blijkt dat dat je een veldje van 5 bij 6 meter in 5×6 blokken van 1 bij 1 meter kunt verdelen; dan wordt vermenigvuldigen ook nuttig bij het berekenen van oppervlakten: oppervlakte=lengte×breedte. Maar voor die lengte en breedte kun je ook andere dan natuurlijke getallen invullen en dan is die vermenigvuldiging nog niet afgesproken. Nog later komen er ook nog negatieve getallen bij en dan kan dat vermenigvuldigen best ingewikkeld worden.
Keith Devlin heeft over dit probleem twee lezenswaardige columns geschreven: It Ain’t No Repeated Addition en It’s Still Not Repeated Addition. Ik ga zijn verhalen hier niet overschrijven maar de essentie is dat optelling en vermenigvuldiging van (reële, complexe, …) getallen twee losse bewerkingen zijn, met als enige verbindende relatie de distributieve wet. Losjes gesproken gaat optellen over toevoegen en vermenigvuldigen over schalen. Als we het over π2 hebben dan bedoelen we dus π geschaald met een factor π en niet zoiets raars als de som van π termen die allemaal gelijk zijn aan π.
En dan hebben we het nog niet over machtsverheffen gehad … Dat leren we in eerste instantie door herhaald vermenigvuldigen maar op een gegeven moment gaat ook dat schuren als we het resultaat van exponentiële groei op niet-rationale tijdstippen willen weergeven.
Eén van mijn favoriete vragen aan eerstejaarsstudenten is naar de definitie van de exponentiële functie 2x; in het bijzonder wat de waarde van 2√2 zou moeten zijn, of beter: hoe je die zou definiëren.
Ik moet bekennen dat ik me in dat artikel aan `herhaald vermenigvuldigen’ heb bezondigd; de juiste definitie van 2x is: de unieke continue functie φ die voldoet aan φ(1)=2 en φ(x+y)=φ(x)×φ(y) voor alle x en y. Lees Analyse Algébrique van Cauchy er maar op na.
Maple en zo, II
“Waarom makkelijk als het moeilijk kan”, lijkt onze vraagsteller gedacht te hebben.
Eigenlijk is het gebruik van Maple en zo een recht dat je moet verwerven.
Maple en zo
Om met een Computer-Algebra-Systeem (CAS) als Maple of Mathematica om te kunnen gaan helpt het als je wat wiskunde beheerst. Dat bleek bijvoorbeeld bij het beantwoorden van een vraag op de wisfaq.
Het begon met deze vraag; daarin kwam een geweldige integraal ter sprake:
![]()
uit de rest van de vraag bleek dat de ondergrens in de integraal ta0 had moeten zijn in plaats van 0. De vraagsteller had dat niet in de gaten en probeerde behulp van het commando piecewise Maple tot het bepalen van de integraal te verleiden. Dat lukte niet.
Bij mijn antwoord op de eerste reactie heb ik, met de hand, de integraal getransformeerd tot een vorm waarin duidelijk werd dat we hier met een getransformeerde β-functie te maken hadden.
De volgende reactie laat zien wat er gebeurt als je niet goed weet wat je doet; het lukte niet de transformatie om te keren.
Twee reacties later leek het verhaal bijna te ontsporen want er kwam een `Gegeneraliseerde β-verdeling’ ter sprake; of het resultaat daar een speciaal geval van was? Door de parameters geschikt te kiezen leek dat wel het geval.
Maar eigenlijk was dat te veel eer; bij de laatste reactie bleek dat om niet veel meer ging dan de dichtheids (p+q)xp+q-1 op het interval [0,1] ging, maar dan getransformeerd.
Wat mij vooral opviel dat er geen enkele poging werd gedaan de Mapleuitvoer een beetje te fatsoeneren of te vereenvoudigen, terwijl dat toch heel wel mogelijk was. En er werd ook geen onderscheid gemaakt (of gezien) tussen hoofd- en bijzaken.
Het Sinterklaasprobleem
Het probleem van vandaag is niet dat van de kleur van de knechten van de Goedheiligman maar dat van het trekken van de lootjes. Wat is de kans dat dat in één keer goed gaat? Kun je het in één keer goed laten gaan?
De kans dat het goed gaat
Als je de namen van alle deelnemers op een papiertje schrijft en daarna iedereen een papiertje uit de hoed (o.i.d.) laat trekken wat is dan de kans dat niemand zichzelf trekt?
Om die kans te kunnen bepalen moet je twee dingen tellen: het totaal aantal manieren waarop de papiertjes uit de hoed getrokken kunnen worden èn het aantal gunstige mogelijkheden. Het laatste aantal gedeeld door het eerste geeft dan de gewenste kans.
Als je dit wiskundig aan wil pakken maak je de situatie zo eenvoudig mogelijk: zet de mensen op een rij, en nummer ze: 1, 2, …, n. Na de trekking zet je persoon i op de plaats van degene die haar getrokken heeft. Op die manier komt een trekking overeen met het op één of andere volgorde zetten van de getallen 1, 2, …, n. Een gunstige trekking is er één waarbij elk getal van zijn (natuurlijke) plaats gehaald wordt.
Je kunt voor kleine n de tellingen met de hand uitvoeren maar het wordt al gauw een beetje onoverzichtelijk: de gevallen n=1 en n=2 zijn een beetje triest, die slaan we maar over. Bij n=3 kunnen we zes trekkingen uitvoeren (schrijf de volgordes maar eens op) en daarvan zijn er twee gunstig: (2,3,1) en (3,1,2). De kans dat het goed gaat is dus 1/3.
Bij een groep van vier mensen zijn er 24 mogelijk trekkingen: de eerste kan vier papiertjes trekken, de tweede drie, de derde twee en de laatste één. Dat levert 4×3×2×1=24 mogelijke volgordes. Het aantal gunstige mogelijkheden is wat lastiger te tellen: je kunt 1 en 2 omwisselen en ook 3 en 4, of 1 en 3 en ook 2 en 4, of 1 en 4 en ook 2 en 3. Dat geeft drie mogelijkheden. Je kunt de getallen ook doorschuiven: zet de mensen in een kring en laat iedereen een positie (naar links) opschuiven; we zetten 1 telkens op dezelfde vaste plek en zetten de andere drie willekeurig neer en dat levert nog zes mogelijkheden. In totaal 9 gunstige rangschikkingen met kans 9/24, ofwel 3/8.
Wie wil puzzelen kan proberen het aantal gunstige rangschikkingen uit de in totaal 5×4×3×2×1=120 manieren om vijf mensen te plaatsen te tellen maar dat wordt al behoorlijk bewerkelijk.
Inclusie-Exclusie
Er is een manier om de telling van het aantal gunstige manieren systematisch te tellen en die manier is ook op veel andere problemen toepasbaar. Het blijkt makkelijker het aantal ongewenste trekkingen te tellen.
Neem een getal n en bekijk de verzameling {1,2,…,n}. Die verzameling kan op n×(n-1)×…×1 manieren gerangschikt worden (het argument hierboven voor n=4 blijft van toepassing). Dat getal noteren we met n! (spreek uit: n-faculteit).
Voor iedere i noteren we de verzameling rangschikkingen die i op haar plaats laten met Di. We willen dus tellen hoeveel elementen er in de vereniging D1∪D2∪…∪Dn zitten.
Voor het gemak voeren we nog de notatie |X| voor het aantal elementen van de verzameling X in.
Teken een plaatje met twee verzamelingen, zeg X en Y, en ga na dat we |X∪Y| als volgt uit kunnen drukken:
|X∪Y|=|X|+|Y|-|X∩Y|
immers: in de som |X|+|Y| tellen we de punten in X∩Y dubbel en daarom moeten we |X∩Y| aftrekken.
Teken een plaatje met drie verzamelingen, X, Y en Z, (met alle mogelijke doorsneden er in) en ga na dat
|X∪Y∪Y∪Z|=|X|+|Y|+|Z|-(|X∩Y|+|X∩Z|+|Y∩Z|)+|X∩Y∩Z|
immers: in |X|+|Y|+|Z| tellen we |X∩Y|+|X∩Z|+|Y∩Z| dubbel, dus dat trekken we af; maar nu zijn de punten in X∩Y∩Z drie keer meegeteld en drie keer afgetrokken, daarom tellen we |X∩Y∩Z| weer op
Als we dit toepassen op het geval n=3 dan krijgen we
|D1|+|D2|+|D3|-(|D1∩D2|+|D1∩D3|+|D2∩D3|)+|D1∩D2∩D3|
als het aantal ongewenste rangschikkingen; omdat |Di|=2 voor elke i, en omdat |Di∩Dj|=1 als i≠j en omdat |D1∩D2∩D3|=1 vinden we 2+2+2-(1+1+1)+1=4 rangschikkingen waarbij ten minste één punt op zijn plaats blijft. We krijgen dus ons eerder gevonden aantal goede rangschikkingen terug.
In het algemene geval gebeurt hetzelfde: eerst de individuele aantallen optellen, dan twee-bij-twee doorsneden aftrekken, drie-bij-drie doorsneden optellen, vier-bij-vier aftrekken …. Dit heet het Principe van Inclusie-Exclusie.
Er zit veel regelmaat in onze aantallen:
- |Di|=(n-1)! (de andere punten mogen willekeurig gerangschikt worden
- |Di∩Dj|=(n-2)! (de andere punten mogen willekeurig gerangschikt worden
- elke k-bij-k doorsnede heeft (n-k)! elementen
Het aantal k-bij-k doorsneden is gelijk aan n!/(k!×(n-k)!) en dat maakt onze berekening heel overzichtelijk: er zijn
![]()
slechte rangschikkingen en dus
![]()
goede rangschikkingen. Als we dat aantal door n! delen komen we uit op een succeskans van
![]()
bij het lootjes trekken met n personen.
Omdat de termen in de som in absolute waarde steeds kleiner worden en beurtelings positief en negatief zijn volgt dat die kans altijd tussen 1/3 en 3/8 zal liggen.
Altijd succes?
Voor wie wil weten hoe je in één keer een goede trekking kunt verrichten: lees deze column van de Wiskundemeisjes uit 2009.
De methode komt er op neer dat je de deelnemers in een kring zet en hun naambriefjes aan de persoon links laat geven (met een truc om het geheim te houden natuurlijk).
Voor wie van puzzelen houdt: vlooi maar eens uit dat de kans dat er bij willekeurig trekken een permutatie als in die column uit komt gelijk is aan 1/n.
Breien en eenheden
Via een tweet van Ionica Smeets kwam ik op deze pagina van de stichting literaire rechten auteurs (lira). Daar word uitgelegd hoe de uitkeringen voor de auteurs berekend worden.
De berekening verloopt als volgt (citaat):
De puntwaarde maakt onderdeel uit van de berekening van de hoogte van de leenrecht-uitkering. De hoogte van de leenrechtuitkering wordt per titel berekend met behulp van een rekenregel die er per uitgeleende titel als volgt uitziet: A×B=C×D=E.
Heh? Wat? Twee producten die aan elkaar gelijk zijn? Nadere uitleg volgt (citaat):
A staat daarin voor het aantal uitleningen dat blijkens de steekproef-gegevens van een boek heeft plaats gevonden. B staat voor de officiële, aan het ISB-nummer gekoppelde verkoopprijs van het boek, bij gebreke waarvan een forfaitaire prijs wordt ingevoerd, dat wil zeggen: ongeveer de gemiddelde verkoopprijs van het boek in Nederland, tot nu toe steeds afgerond op 25,-. C is het product van A en B en staat voor het aantal punten dat aan deze uitleningen van deze titel wordt toegekend. D staat vervolgens voor het bedrag per punt. Dit bedrag per punt (de puntwaarde) wordt separaat berekend door het totaal aantal binnen de steekproef geconstateerde uitleningen te vermenigvuldigen met de som van alle in het systeem aanwezige verkoopprijzen en de uitkomst daarvan te delen op het totaal van het netto voor uitkering beschikbare bedrag. E tenslotte is het bedrag dat per uitgeleende titel naar gelang het aantal uitleningen en de verkoopprijs als slotsom wordt berekend.
Juist ja, ordinair breiwerk dus: C=A×B en E=C×D, kortom E=(A×B)×D.
Eenheden
Het betrof hier een klacht over vooral die laatste factor D, de puntwaarde, dat begrip werd onduidelijk gevonden. Ik heb de beschrijving van dat ding een paar keer gelezen en ik ben nog niet veel wijzer, ik zie drie dingen
- het totaal aantal binnen de steekproef geconstateerde uitleningen
- dat lijkt verdacht veel op A. Het zou echter ook kunnen zijn dat A een schatting van het totaal aantal uitleningen is, gebaseerd op het onderhavige aantal maar dat had dan wat duidelijker uitgelegd mogen worden.
- de som van alle in het systeem aanwezige verkoopprijzen
- was er een lijst van alle mogelijke bedragen die optreden als prijs van een of ander boek en zijn die bedragen bij elkaar opgeteld? Waarom zou je dat in vredesnaam doen? Ik hoop dat er iets zinvollers werd bedoeld maar ik zou niet weten wat.
- het totaal van het netto voor uitkering beschikbare bedrag
- de woorden `het totaal van’ lijken me hier overbodig
Ik zie hier dus drie grootheden: een aantal, laten we dat n noemen; een bedrag, laten we dat B1 noemen; en nog een bedrag, zeg B2. Uit de beschrijving haal ik dat D gelijk is aan (n×B1)/B2 (of misschien aan B2/(n×B1), want je weet maar nooit wat `delen op’ betekent, ik deel liever door). Maar, hoe dan ook, in tegenstelling tot wat geschreven wordt is de puntwaarde D geen bedrag: D is een dimensieloos getal. De berekening geeft namelijk [getal]×[gulden]/[gulden] (het stuk is uit 2001) en daarin strepen we de guldens tegen elkaar weg.
Ik hoop dat de klager nogmaals geklaagd heeft want deze uitleg was niet best.
Twee keer zo langzaam; de helft langzamer
“Twee keer zo langzaam” betekent hetzelfde als “de helft langzamer”.
Via een tweet van Enith Vlooswijk vond ik deze deze gedachtenwisseling:
Vraag: ‘2 keer zo langzaam’ hoor je vaak, maar is het correct en/of betekent het iets?
Antwoord: Ja, het is correct. Je zou ook kunnen zeggen: ‘de helft langzamer’; dat betekent hetzelfde.
Dit klinkt als iets waar ik het in een eerdere blogpost ook al eens over heb gehad: het door elkaar halen van `twee keer zo X’ en `de helft X-er’. Dat is vaak een gevolg van het door elkaar halen van Begin- en Eindsituatie. In symbolen: `twee keer zo X’ kun je schrijven als E=2B en `de helft X-er’ kun je schrijven als E=B+E/2. In het eerste geval verdubbel je B, en in het tweede geval tel je de helft van E op bij B om E te krijgen. Voor de gewenste ondubbelzinnigheid: werk altijd vanuit de beginsituatie; de juiste betekenis van `de helft X-er’ is daarmee dus E=B+B/2.
In dit geval is er echter nog iets aan de hand. We kijken eerst even in het woordenboek voor de betekenis van langzaam:
- niet vlug; traag, sloom
- met geringe snelheid
- in de vergrotende trap ter aanduiding van een geringere snelheid in relatieve zin
- zonder snelle overgang of ontwikkeling; geleidelijk
In alle gevallen staat er iets dat eigenlijk niet te kwantificeren is: hoe meet je of iets twee keer zo ‘niet vlug’ is als iets anders? En wat te denken van een twee keer zo geringe snelheid of iets waarvan de snelheid de helft geringer is?
En verder: wanneer is iets langzaam genoeg om deze constructies te kunnen gebruiken? Ik neem aan dat “twee keer zo langzaam als de lichtsnelheid” niet alleen mij de wenkbrauwen doet fronsen?
Misschien wordt daarom het antwoord op de vraag of `2 keer zo langzaam’ iets betekent niet expliciet maar impliciet gegeven: “hetzelfde als `de helft langzamer'”. En ik ben dan geneigd te zeggen: inderdaad, de twee constructies betekenen hetzelfde, namelijk niets.
Nu kan ik wel raden wat de gedachte betekenis van `2 keer zo langzaam’ is: met de halve snelheid. En dan kun je `de helft langzamer’ ook wel duiden: ga langzamer en wel met de helft van de huidige snelheid.
Maar waarom zou je dat dan niet gewoon zeggen?
Toch wat wiskunde
Als we `twee keer zo langzaam’ als `half zo snel’ interpreteren dan komen we uit op de volgende `Behoudswet’: het product van snelheid en langzaamheid is constant. Maar dan betekent `de helft langzamer’ toch echt `twee keer zo snel’.
De ene wortel is de andere niet
Of toch wel …
Er was weer een interessante vraag op de wisfaq. OK, wiskundig gezien niet erg interessant maar wel als inkijk in het hoofd van een/de(?) student.
Een vraag over de cosinus van de helft van arcsin(⅓) leidde tot het volgende: de student had
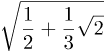
als antwoord gevonden en het `officiéle’ antwoord was
![]()
In de woorden van de student: “En dat is waar ik vastloop.”.
Eigenlijk was de student niet vastgelopen; de oplossing was correct, alleen niet letterlijk gelijk aan het modelantwoord. Voor iemand die met vierkantswortels om kan gaan zou het een koud kunstje moeten zijn het ene antwoord in het andere om te zetten en ik vraag me af waarom dat tot `vastlopen’ zou moeten leiden.
De oefening ging duidelijk om werken met inverse goniofuncties en daar kan de student mee overweg. Hij is kennelijk de routine van de vierkantswortels al weer kwijt. En uit de vervolgvraag blijkt dat hij niet erg stevig in de schoenen staat.
De vraag is wat de vraag is geweest: als er niets meer gevraagd werd dan de cosinus van de helft van arcsin(⅓) dan is het antwoord van de student prima; het modelantwoord is alleen wat mooier gemaakt. Al kun je daar over twisten: aan het antwoord van de student is wat makkelijker te zien hoe groot die cosinus ongeveer is. Als in de vraag stond dat in de wortel alleen gehele getallen mogen staan dan is het modelantwoord het gewenste antwoord maar dan gaat de vraag over meer dan alleen goniofuncties.
Dit alles neemt niet weg dat je van een student zou mogen verwachten dat deze in staat zou moeten zijn de twee wortelvormen aan elkaar gelijk te praten.

Recent Comments