KP Hart
KP checkt: Hartslag en de Gulden Snede
In deze blogpost beschreef ik een artikel waarin metingen aan mensenschedels moesten aantonen dat een aantal maten zich volgens de Gulden Snede zouden verhouden. De conclusies waren nogal discutabel maar ook al waren de getallen niet echt dicht bij de Gulden Snede ze leken tenminste te kloppen. In de referenties van het artikel vond ik veel verwijzingen naar andere voorkomens van de Gulden Snede. Twee daarvan heb ik nader bekeken: Golden Ratio is beating in our heart en Does systolic and diastolic blood pressure follow Golden Ratio. Daar kloppen de getallen iets minder goed.
Kloppende getallen
Wat bedoel ik met `kloppende getallen’? Welnu, als je een lengte, zeg A, in twee stukken verdeeld, zeg B en C, dan geldt natuurlijk A=B+C. Als je op jacht bent naar de Gulden Snede neem je de grootste van de twee stukken, zeg C, en dan bekijk je de verhoudingen A/C en C/B. Je hoopt dat die verhoudingen gelijk zijn want dan heb je de Gulden Snede te pakken.
Tussen die twee verhoudingen bestaat een relatie: deel de gelijkheid maar door C dan krijg je A/C=B/C+1, of iets ingewikkelder opgeschreven: A/C=1/(C/B)+1. Als we onze twee verhoudingen even afkorten, A/C=y en C/B=x, dan staat hier y=1/x+1.
Anders gezegd: het punt met coordinaten (C/B,A/C) ligt op de grafiek van y=1/x+1.
In het artikel Mammalian Skull Dimensions and the Golden Ratio worden de volgende gemiddelden van de verhoudingen gerapporteerd: A/C=1.64 ± 0.04) en C/B=1.57 ± 0.10 (de letters zijn anders, maar het gaat om de getallen).
Niet alleen het punt (1.57,1.64) ligt op de grafiek van y=1/x+1 maar ook de punten (1.47,1.68) en (1.67,1.60); deze worden bepaald door de randpunten van de intervallen (1.60,1.68) (voor A/C) en (1.47,1.67) (voor (C/B). Zie het plaatje hieronder.
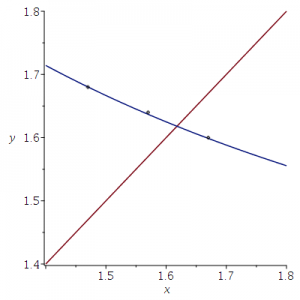
Dit bedoel ik met kloppende getallen: de resultaten horen in ieder geval bij de stituatie waar A=B+C.
Overigens laat ik het aan de lezer om te beoordelen, gezien dit plaatje, in hoeverre deze conclusie gerechtvaardigd is:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Het snijpunt van de twee grafieken (y=1/x+1 en y=x) is het punt (Φ,Φ), en daar ligt (1.57,1.64) toch nog wel ver vandaan.
Hartslag en bloeddruk
In de referenties van het schedelartikel vond ik de artikelen die hierboven genoemd werden.
Hartslag
Om te beginnen: in Golden Ratio is beating in our heart wordt de Gulden Snede ontdekt in verhoudingen van tijdsintervallen in de hartslag. Een mooi plaatje met een uitleg van alle termen staat op de wikipedia-pagina over het QRS-complex:

De drie grootheden waar het hier om gaat zijn: (A) het R-R-interval (tussen twee opeenvolgende R-en), (B) de systole (samentrekfase), en (C) de diastole (ontspanningfase).
De letters komen overeen met onze eerste paragraaf en met de verhoudingen waar het artikel over gaat.
De resultaten zijn
- A=866 ± 73
- B=333 ± 22
- C=536 ± 66
- C/B=1.611
- A/C=1.618
Deze getallen zijn problematisch.
Ten eerste tellen de gemiddelde waarden niet goed op: A=866 en B+C=869. Dat zou wel moeten als alle metingen goed waren dan geldt A=B+C voor elke meting en dan ook voor de gemiddelden.
Ten tweede: als een van de verhoudingen gelijk is aan Φ dan is de andere dat ook, hier is dat niet zo.
Ten derde: als je, net als in het schedelmetingartikel, de verhoudingen van de gemiddelden neemt kom je op andere getallen uit: 866/536=1.61567 en 536/333=1.6096.
Het zou kunnen zijn dat de gerapporteerde verhoudingen gemiddelden zijn van de verhoudingen per meting maar dan hadden de auteurs dat wel even mogen vermelden.
Voorlopig geloof ik niets van de conclusies van het artikel.
Het lijkt er op dat de individuele verhoudingen wel zijn uitgerekend want het artikel bevat nog een niet-ter-zake-doende grafiek waarin de verhouding C/B is uitgezet tegen de hartslag.

Daar is in ieder geval te zien dat de verhouding C/B behoorlijk variabel is.
Bloeddruk
In het artikel Does systolic and diastolic blood pressure follow Golden Ratio gaat het om de bloeddruk. De grootheden zijn nu: (A) de systolische druk (bovendruk), (C) de diastolische druk (onderdruk), en (B) hun verschil; alle in mm Hg.
| A | C | B | A/C=y | C/B=x | |
|---|---|---|---|---|---|
| etmaal | 137 ± 16 | 86 ± 12 | 51 | 1.59 | 1.69 |
| dag | 140 ± 17 | 89 ± 12 | 51 | 1.57 | 1.75 |
| nacht | 131 ± 18 | 80 ± 13 | 51 | 1.64 | 1.62 |
Wat hier opvalt is dat er voor het verschil geen interval is opgegeven; alsof het bij alle metingen precies 51 mm Hg was (dat geloof ik dus niet). De verhoudingen komen hier wel voort uit de gemiddelden behalve de verhouding C/B in de nacht: 80/51=1.56862. Laat die foute 1.62 nou net de verhouding zijn die het dichtst bij de Gulden Snede ligt.
Ik heb de punten vergeleken met de grafiek van y=1/x+1.
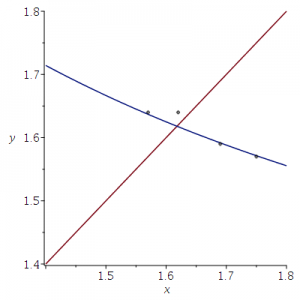
De twee punten rechts horen bij de verhoudingen voor een etmaal en overdag. Het meest linkse punt hoort bij de echte nachtelijke verhoudingen. Het punt dat ruim boven de grafiek ligt hoort bij de gerapporteerde nachtelijke verhoudingen. Ik heb geen idee hoe dat gebeurd kan zijn.
Daar is-tie weer: de Gulden Snede
Niet uit te roeien, die Gulden Snede: via een stukje op Science Alert kwam ik hier: Mammalian Skull Dimensions and the Golden Ratio.
Wat staat er in dat artikel?
Welnu over je schedel loopt een lijn, van het Nasion (N) naar het Inion (I); op die lijn ligt een punt het Bregma (B) geheten. Op honderd mensenschedels zijn de lengten NI, NB en BI gemeten (niet letterlijk, er is gemeten aan hoge-resolutiescans van schedels). Nu geldt, natuurlijk, NB+BI=NI en verder is het deel BI wat groter dan het deel NB.
Op zoek naar de Gulden Snede hebben de auteurs van elke schedel de verhoudingen NI/BI en BI/NB bepaald. Als B de lijn NI inderdaad volgens uiterste en middelste reden verdeelt, dan verwachten we dat NI/BI gelijk is aan BI/NB.
Na middelen en standaard-deviatie nemen komen de auteurs uit op NI/BI = 1.64 ± 0.04 en BI/NB = 1.57 ± 0.10. In de woorden van de auteurs:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Ik weet niet wat de lezer denkt maar in vind dat een krasse uitspraak. De gemiddelden liggen nogal ver uit elkaar. Of je nu vanuit 1.64 of vanuit 1.57 rekent, het verschil is relatief meer dan 4%. Dat lijkt me niet `essentially identical’. Ik denk dat de wens hier toch de vader van de gedachte is geweest.
Overigens zijn de opgegeven waarden wel consistent met de betrekking die tussen de verhoudingen moet gelden: door de gelijkheid NB+BI=NI door BI te delen ontstaat de gelijkheid NI/BI = 1/(BI/NB)+1. Om dit iets overzichtelijker te maken noemen we NI/BI even y en BI/NB even x, de gelijkheid wordt dan y=1+1/x. De punten (1.57,1.64), (1.47,1.68) en (1.67,1.60) liggen op een haar na op de grafiek van deze vergelijking.
Deze betrekking verklaart ook de volgende observatie van de auteurs:
Interestingly, the reciprocal of Φ (1/Φ or 1/1.61803…) is 1 integer less than Φ (0.61803…) and has the same decimal extension as Φ, and the square of Φ (Φ² or 1.61803…2) is 1 integer more than Φ (2.61803…) and also has the same decimal extension.
Uhm, ja, nogal wiedes; de verdeling in uiterste en middelste reden dicteert dat Φ aan de gelijkheid Φ=1+1/Φ moet voldoen, en dus ook aan Φ²=Φ+1. Iedere middelbare-scholier die kwadratische functies heeft gezien kan je dit uitleggen.
Ten slotte
Het artikel beslaat negen kolommen; daarvan zijn er vier gevuld met een verslag van de metingen; er is ook aan zes andere zoogdiersoorten gemeten en het lijkt er op dat bij toenemende `complexiteit’ van de soort de verhouding NI/BI daalt en BI/BN dus stijgt. De (speculatieve) uitleg is dat gaande de evolutie de schedel op deze manier bij bepaalde kwabben is gaan passen.
Als de auteurs zich nu maar bij deze conclusie hadden gehouden dan was er weing mis geweest met dit artikel. De overige vijf kolommen zijn echter gevuld met niet ter zake doende beschrijvingen van de Gulden Snede, de relatie met de rij van Fibonacci, en het vermeende optreden van dit getal bij allerlei fysiologische en morphologische verschijnselen.
Allerlei al lang onderuit gehaalde mythes over de Gulden Snede worden weer van stal gehaald en als belangwekkende feiten gepresenteerd.
In het fraaie boek De Ontstelling van Pythagoras heeft Albert van der Schoot vrijwel niets heel gelaten van alle flauwekul die over de Gulden Snede verteld wordt. De recensie in NRC noemt er al een paar. En lees ook het artikel Het is niet alles goud wat er snijdt van Van der Schoot in het Nieuw Archief voor Wiskunde.
Ook deze column van Keith Devlin is het lezen meer dan waard.
Metaforen? Liever definities.
Bij uitleg van niet-triviale wiskundige resultaten grijpt men nogal vaak naar een of andere metafoor, waarschijnlijk omdat de echte context te moeilijk voor de lezer wordt gevonden. Dat leidt vrijwel altijd tot onbegrip of erger nog tot slecht begrip. Een extreem voorbeeld was onlangs te vinden in NewScientist.
In bovenvermeld stuk werd melding gemaakt van een, ook voor de gemiddelde wiskundige, niet-triviaal resultaat — de formulering was in de vorm van een metafoor over een oneindige versie van de lotto. Die was zo onduidelijk dat ik aan het eind van het stuk nog steeds niet wist niet wat het wiskundige resultaat was (of zelfs waar het over ging); pas na doorklikken naar het echte artikel herkende ik het als iets dat ik in april al voorbij had zien komen. De reacties onder het stuk laten zien dat er meer lezers waren die niet begrepen hadden waar het over ging.
Nadat ik mijn blogposts (deze en deze) op facebook had gezet schreef een collega dat de opsteller van het oorspronkelijke probleem (Adrian Mathias) zelf de lotto-metafoor had verzonnen.
Het probleem van het stuk in NewScientist (en het het origineel) was ook nog dat de uitleg niet volledig was: het was niet duidelijk hoe de lottoformulieren in te vullen en er werd al helemaal niet vermeld hoe je zou kunnen winnen.
Ik heb zelf maar een lotto verzonnen en aan twitter gevraagd welke uitleg beter was: zakelijk of metaforisch.
Welke uitleg is beter
— (((K P Hart))) (@hartkp) September 20, 2019
De uitslag was overweldigend: 100% vond de zakelijke uitleg beter. Ik geef toe: drie stemmen is niet veel, maar er moest dan ook wel veel gelezen worden.
Het wiskundige resultaat ging over families oneindige deelverzamelingen van de verzamelingen der natuurlijke getallen. In deze blogpost staat meer informatie; het kost waarschijnlijk enige moeite alles te verstouwen maar ik heb de illusie dat heze uitleg beter is dan een gekunstelt verhaal over de lotto.
Het oneindige fascineert velen, dat is zelfs te zien geweest in de Nationale Wetenschapsagenda. Veel vragen gingen eigenlijk over de metaforen die gebruikt zijn om `oneindig’ uit te leggen en hadden dus eigenlijk in het geheel geen wiskundige inhoud. En dat vind ik dus jammer. De wiskunde van het oneindige is te mooi om in verhullende verhalen te verstoppen. Wie mij over oneindig wil laten praten krijgt de definities om de oren (en het helpt als je vantevoren deze wikipediapagina goed bestudeert.
U bent gewaarschuwd.
Strictly between
This is the third in a short series of blog posts intended to explain the terms in red in the following sentence, that succinctly describes the Continuum Hypothesis.
There is no set whose cardinality is strictly between that of the integers and the real numbers.
These are, in the words of John Lloyd, the bits that he does not understand.
Thus far we have dealt with set in this post and this one, and with the notion of cardinality in this one.
To recap our findings: we first came to the disappointing realisation that the definitions proposed by Georg Cantor, very strictly speaking, did not deliver on their promises. There is a way out of this via the development of Axiomatic Set Theory but that would take us too far afield.
In the spirit of Cantor we can define a set to be a well-defined collection of objects as long as we furnish a good description/definition of that collection.
As to cardinality: we consider it a property that every set has and that leads to two derived properties of pairs of sets that are defined unambiguously.
Two sets, X and Y, are said to have the same cardinality if “it is possible to put them, by some law, in such a relation to one another that to every element of each one of them corresponds one and only one element of the other” (Cantor, translation by Jourdain). We simply abbreviate this as |X|=|Y|. Additionally we can define what |X|≤|Y| (“the cardinality of X is less than or equal to that of Y”) means that there is a subset Z of Y such that |X|=|Z| (“X has the same cardinality as some subset of Y”).
In this post there are some examples of sets with the same cardinality (provinces of the Netherlands, and months of the year) and with different cardinalities (two teaspoons of chocolate sprinkles).
It is now actually quite straightforward to come to the definition of strictly between. First we define `strictly less’; then `strictly between’ is a combination of twice `strictly less’.
In the example of the chocolate sprinkles the cardinality of the sprinkles in the left hand spoon was strictly less that the cardinality on the right hand side. I paired off the sprinkles on the left with a subset of the sprinkles on the right and it was at once clear that there was no way to pair off both sets with each other. In short, we saw that |L|≤|R| and that |L|≠|R|. And this will be our definition of “the cardinality of X is strictly less than that of Y”, in symbols |X|<|Y|: it is the conjuction of |X|≤|Y| and |X|≠|Y|.
Cantor’s seminal theorem from 1873 can be summarized as |N|<|R|, where N and R denote the sets of natural and real numbers respectively (more on the definition of these in later posts).
Since N is a subset of R it is clear that |N|≤|R|; the hard part of Cantor’s proof was to show that |N|≠|R|, i.e., that there is no way to pair off the natural numbers and the real numbers with each other.
So “the cardinality of Y is strictly between the cardinalities of X and Z” is the conjuction of |X|<|Y| and |Y|<|Z| and ultimately comes down to the following four statements:
- X can be put into one-to-one correspondentce with a subset of Y,
- Y can be put into one-to-one correspondentce with a subset of Z,
- X cannot be put into one-to-one correspondentce with Y, and
- Y cannot be put into one-to-one correspondentce with Z
For explicitly given sets it is often not too difficult to establish whether this state of affairs holds or not; certainly not with all the tools that Cantor and his followers have developed.
In the case of the Continuum Hypothesis matters lie differently: two of the three sets are there; one should produce the third in the middle, or show that no third exists. At the beginning of the 20th century either possibility probably seemed like an insurmountable task, although Cantor strongly believed in the second alternative.
Loterijen? Eerder de Lotto.
Gisteren, in het stuk over bijna-disjuncte families, heb ik het niet over de loterijen gehad waar het in stuk in NewScientist over ging. Sommige mensen waren benieuwd naar die metafoor voor het resultaat in het artikel van David Schrittesser en Asger Törnquist. Ik doe hier een poging zo’n loterij te beschrijven. Ik laat het aan de lezer om te beoordelen welke uitleg beter is: de feitelijke in de vorige post of de metaforische hieronder.
Om te beginnen: `loterij’ is eigenlijk een verkeerde vertaling van het Amerikaanse `lottery’. Bij een loterij koop je een lot en weet je niet wat je lotnummer zal zijn. In een lottery kies je zelf de getallen op je kaartje. Het is dus eerder te vergelijken met onze Lotto. De beschrijving van de `loterij’ in NewScientist is ook eerder die van een variant op de Lotto dan op de Staatsloterij.
Een oneindige variant op de Lotto
In plaats van 6 uit 45 kiezen we getallen uit N. Met de betekenis van het woord `bijna’ van gisteren in gedachten leggen we vast dat we niet `bijna niets’ en ook niet `bijna alles’ mogen kiezen: we moeten er oneindig veel kiezen (aankruisen) en we moeten er oneindig veel niet aankruisen.
Een `formulier’ heeft dus oneindig lange kolommen (net zo lang als N) en oneindig veel kolommen. Je mag dus, kennelijk, oneindig veel kolommen invullen. Wat in het stuk niet duidelijk vermeld wordt is hoe je een prijs kunt winnen.
Maar met het artikel in de hand kunnen we wel wat regels opstellen. Het artikel bewijst namelijk dat oneindige maximale bijna-disjuncte families niet bestaan (dat `oneindige’ heb ik gisteren voor het gemak weggelaten maar dat wordt nu belangrijk); het stukje zegt dat er geen winnende formulieren bestaan. Conclusie: een (zeker) winnend formulier heeft in de kolommen een oneindige maximale bijna-disjuncte familie.
Daaruit concluderen we dan dat een winnende kolom een oneindige doorsnede heeft met de getrokken deelverzameling van N.
We halen hier ook nog wat voorwaarden uit waaraan een geldig formulier aan moet voldoen: niet alleen mag je in één kolom niet bijna alle getallen aankruisen, ook mag je er niet voor zorgen dat je over een eindig aantal kolommen bijna alle getallen aankruist. Als je bijvoorbeeld over tien kolommen achtereenvolgens de tienvouden, tienvouden-plus-1, … tienvouden-plus-9 aankruist win je ook zeker; die tien verzamelingen vormen een eindige maximale bijna-disjuncte familie.
Samengevat: op je formulier kruis je in een aantal kolommen telkens oneindig veel getallen aan. Dat aantal kolommen mag eindig zijn maar hoe dan ook: in elke eindige greep kolommen mag je nooit samen bijna alle getallen aankruisen. Je wint als je in ten minste één kolom oneindig veel getrokken getallen hebt aangekruist.
Door je kolommen bijna-disjunct in te vullen spreid je je inzet het zuinigst; twee kolommen met een oneindige doorsnede hebben een grote overlap aan mogelijkheden. Ten slotte: als je kolommen een maximale bijna-disjuncte familie vormen dan bevat je formulier, per definitie, een winnende kolom.
Het bestaan van (zuinige) winnende formulieren
Het stuk in NewScientist vertelt niet de hele waarheid. De suggestie wordt gewekt dat winnende formulieren niet bestaan. Dat is slechts voor de helft waar. Je kunt bewijzen dat zeker winnende en zuinige formulieren bestaan, met behulp van het Lemma van Zorn (een equivalent van het Keuzeaxioma).
Sommige wiskundigen vragen zich in dit soort situaties af of het Lemma van Zorn wel nodig is bij zo’n concrete vraag; dat Lemma levert namelijk nogal zwaar geschut. En dat is nu wat David Schrittesser en Asger Törnquist hebben vastgesteld: je hebt zwaar geschut nodig; er is bestaat een situatie waarin dat zware geschut niet voorhanden is en waarin geen enkele maximale bijna-disjuncte familie bestaat.
Loterijen? Nou, nee.
Vanochtend (2019-09-19) vond ik via twitter dit artikel uit NewScientist (een vrij letterlijke vertaling van dit stuk. Nadat ik het verhaal over niet-bestaande oneindige loterijen had gelezen was ik nog niets wijzer geworden. Na doorklikken naar het originele artikel zag ik dat ik het al eerder had gezien in april, op ArXiV.org en dat het niets met loterijen te maken had.
Maar waar gaat het artikel dan wel over? Over bijna-disjuncte families. En wat zijn dat nu weer?
Eén van mijn favoriete objecten in de verzamelingenleer is de familie van alle deelverzamelingen van de verzameling N der natuurlijke getallen. Dit is een nimmer opdrogende bron van vragen en resultaten die in veel delen van de wiskunde gebruikt worden maar die gewoon ook leuk zijn om aan te werken.
Hierbij is het bijwoord `bijna’ bijna niet te vermijden. In het artikel waar we het hier over hebben past men `bijna’ dus toe op `disjunct’. Nu noemen we twee verzamelingen A en B `disjunct’ als hun doorsnede leeg is, A∩B=∅, als er geen x is die zowel in A als in B zit.
Het woord `bijna’ kort eigenlijk het wat uitgebreidere `op eindig veel na’ af: twee verzamelingen zijn bijna disjunct als hun doorsnede eindig is — `hun doorsnede is op eindig veel elementen na leeg’. Hierbij eisen we wel dat de verzamelingen zelf oneindig zijn want anders is bijna-disjunctheid niet zo spannend.
De twee verzamelingen E en O van respectievelijk de even en oneven getallen zijn disjunct; er is geen natuurlijk getal van tegelijk even en oneven is.
Hier is een mooie truc, van Sierpinski uit 1928: voor elk positief irrationaal getal x en voor elk natuurlijk getal n doen we het volgende: bepaal n×x, neem het gehele deel [n×x] (gooi alles achter de komma weg) en deel dat weer door n.
Bij vaste x krijg je zo een rij rationale getallen: [x], [2x]/2, [3x]/3, [4x]/4, … Bij π bijvoorbeeld krijgen we zo 3, 3, 3, 3, 3, 3, 3, 25/8, 28/9, 31/10, 34/11, 37/12, …
Uit de definitie van de rij volgt dat 0<x-[n×x]/n<1/n voor alle n en dit betekent iets voor de bijbehorende verzamelingen termen. Bij elke x stoppen we de termen van de rij in de verzameling Sx, dus Sπ={3, 25/8, 28/9, 31/10, 34/11, 37/12, …}.
Neem nu eens twee irrationale getallen x en y met x<y; dan geldt voor n>1/(y-x) dat [n×y]/n>y-1/n>x, en dus zit [n×y]/n niet in Sx. We concluderen dat de verzamelingen Sx en Sy bijna disjunct zijn.
De verzamelingen Sx vormen het soort familie waar het artikel over gaat: een bijna-disjuncte familie, elk tweetal elementen is bijna disjunct (en elke Sx heeft oneindig veel elementen).
Het voorbeeld van Sierpinski laat zien dat er een groot verschil is tussen `disjunct’ en `bijna disjunct’. Als een familie disjunct is dan zit elk punt in ten hoogste één element van de familie. De bijna-disjuncte familie van Sierpinski bestaat uit verzamelingen rationale getallen, daar zijn er evenveel van als natuurlijke getallen. De familie zelf heeft evenveel elementen als er positieve irrationale getallen en dat zijn er veel en veel meer als er natuurlijke getallen zijn (en dat is allemaal precies te maken). Dat zorgt er voor dat veel van de rationale getallen in meer dan één verzameling Sx zitten.
Maar goed, terug naar het artikel. Het hoofdresultaat zegt iets over de aard van bijna-disjuncte families deelverzamelingen van N: onder bepaalde omstandigheden is er geen maximale bijna-disjuncte familie. Als je zo’n familie hebt kun je er een oneindige deelverzameling van N bij doen zó dat de grotere familie ook bijna-disjunct is (en nog één, en nog één, …).
Wat dit nou met loterijen te maken heeft? Ik zou willen zeggen dat ik geen idee heb maar dat heb ik wel. Ik vind de vergelijking echter zó vergezocht dat ik de lezer er niet mee lastig wil vallen. En ik denk eigenlijk dat de uitleg van die vergelijking lastiger is dan die van het resultaat zelf.
Birthday Paradox on steroids.
Most of us are familiar with the so-called Birthday Paradox: the probability in a group of 23 people there are (at least) two who share a birthday is larger than 50%. If you are not familiar with this result then you could peek at the calculation on the Wikipedia page or try it for yourself (big hint calculate the probability that no two people in the group share a birthday).
In Act One of Episode 630 of This American Life we see another take on this phenomenon. It occurs in the context of voter fraud, in particular double voting. In this case, a bit simplified, one looks at the probability that in the group of American Voters two of them would have the same name and the same birthday (including the year).
Listen to the episode to see that basically all cases of `double voting’ can be accounted for by chance alone. And then you may want to read the paper on which the item was based, and visit the website of Sharad Goel (who was featured in the broadcast).
Upgoer Five
Today I was reminded of the Upgoer Five Editor, which was inspired by this XKCD cartoon (an explanation of the workings of the Saturn V rocket in very simple words).
I knew I had tried it once and thanks to twitter I could find my `explanation’ of bijections and a `definition’ of infinity again. This is just a short post so that I have an obvious place to look for the link to that short piece, when I need it.
Also, it will be fun to do this in Norwegian.
Dikke en dunne verzamelingen
Gisteren hebben we gekeken naar de wiskunde achter het vermoeden van Duffin en Schaeffer. Wat daar niet goed uit de verf kwam waren de noties van `dikke’ en `dunne’ verzamelingen. Daar doen we vandaag wat aan.
Zoals gisteren en in de krant beschreven gaat het vermoeden van Duffin en Schaeffer over benaderingen van irrationale getallen met behulp van breuken. De situatie is als volgt: neem een rij (xn)n van positieve reële getallen en noem een irrationaal getal α goed benaderbaar, volgens de gegeven rij, als er oneindig veel natuurlijke getallen n bestaan met voor elk van die n een breuk t/n met noemer n bestaat zó dat |α-t/n|<xn.
De vraag is dan natuurlijk of er irrationale getallen zijn die goed te benaderen zijn. Gisteren hebben we gezien dat als x_n=n-2 alle irrationale getallen goed te benaderen zijn. Met een beroep op de gisteren ook genoemde Categoriestelling van Baire kunnen we laten zien dat er altijd heel veel goed benaderbare irrationale getallen zijn. Net als gisteren bekijken we voor elke n de intervallen (0,xn), (1/n-xn,1/n+xn) … (1-1/n-xn,1-1/n+xn), (1-xn,1). Hun vereniging noemen we An.
Neem een (klein) interval (a,b) binnen (0,1); dan geldt voor elke n met 1/n<b-a dat An en (a,b) een niet-lege doorsnede hebben (bedenk maar eens waarom dat zo is). Dit betekent dat indien we voor elke n de verzamelingen An, An+1, An+2, … verenigen tot de verzameling On we een verzameling krijgen die met elk intervalletje getallen gemeen heeft. De stelling van Baire garandeert nu dat er heel veel getallen bestaan die tot alle On behoren, en dus tot oneindig veel van de An (denk daar ook maar eens goed over na). Al die getallen zijn dus goed benaderbaar, volgens de gegeven rij.
In topologische zin is het complement van die verzameling goed benaderbare getallen nogal dunnetjes, in het Engels: meagre; de verzameling goed benaderbare getallen is dus, topologisch gesproken, bijna het hele interval (0,1) een dikke verzameling dus.
Het vermoeden van Duffin en Schaeffer ging over een andere notie van dik en dun. Laten we de verzameling goed benaderbare getallen, bij de rij (xn)n, even noteren met G(x). De nu bewezen stelling kijkt naar de (totale) lengte van de intervalletjes die we hierboven gebruikt hebben. Voor elke n is de totale lengte van An gelijk aan 2×n×xn. Als de xn-en te klein zijn zal de verzameling G(x) volgens deze notie als dun aangemerkt worden in die zin dat de kans dat een irrationaal getal goed benaderbaar is gelijk is aan 0.
De stelling van Dimitris Koukoulopoulos en James Maynard spreekt uit dat voor elke rij (xn)n de verzameling G(x) hetzij kans gelijk aan 1 heeft om geraakt te worden, hetzij kans 0; een tussenweg is er niet. Daarnaast geeft de stelling precies aan voor welke rijen kans 1 geldt en voor welke rijen kans 0.
We hebben hier dus twee soorten `dik en dun’ gezien: topologisch en kanstheoretisch. Beide noties worden in de Analyse toegepast om te laten zien dat bepaalde objecten bestaan: als je laat zien dat de verzameling van die dingen `dik’ is is die zeker niet leeg.
Voor topologen is de verzameling goed benaderbare getallen altijd `dik’; voor kansrekenaars is hij soms `dik’ en soms `dun’. Dit klinkt paradoxaal, maar is het niet: het is `gewoon’ een gevolg van de definities. En het illusteert wel treffend de titel van de column die gisteren is aangehaald: ‘De kans is nul’ is niet hetzelfde als ‘dat gaat niet gebeuren’.
Het vermoeden van Duffin en Schaeffer
Recentelijk is het Duffin-Schaeffer-vermoeden bewezen. U kunt de preprint hier lezen. In de krant is er ook aandacht aan besteed. Ik wil hier iets meer over de wiskunde achter dit vermoeden vertellen.
Het vermoeden, nu dus een stelling, zegt iets over het benaderen van irrationale getallen met behulp van rationale getallen. De vraag is in het algemeen hoe efficiëent dergelijke benaderingen kunnen zijn.
Nu zullen de meningen over wat efficiënt is uiteen lopen maar de benaderingen die we in de praktijk gebruiken, namelijk afgekapte decimale ontwikkelingen, zijn het niet echt. Als die afgekapte ontwikkelingen als breuk schrijft is die breuk vrijwel nooit te vereenvoudigen: de benadering 3.14159265358979323846264338327 van π levert een onvereenvoudigbare breuk met een grote teller en een grote noemer.
Een goede benadering is er een waar de nauwkeurigheid groot is, vergeleken met de grootte van teller en noemer. Zo kun je 22/7 een goede benadering van π noemen omdat het verschil 22/7-π kleiner is dan 1/49. Het criterium dat we hier hanteren is: p/q is een goede benadering van α als |α-p/q| kleiner is dan 1/q2. Overigens is 19/6 ook een goede benadering: 19/6-π is kleiner dan 1/36.
Een beetje spelen met een rekenmachientje laat zien dat er geen goede benaderingen van π zijn met noemers 8 of 9.
Het vermoeden van Duffin en Schaeffer, nu dus de stelling van Dimitris Koukoulopoulos en James Maynard, gaat overigens niet over individuele irrationale getallen als π of √2. Het bekijkt de zaak van de andere kant en doet uitspraken over hoeveel irrationale getallen veel goede benaderingen hebben.
Je kunt bijvoorbeeld een vaste noemer n nemen en kijken welke getallen een goede benadering met noemer n hebben. Hierbij beperken we ons tot het interval (0,1); getallen in andere intervallen krijgen we door over een geheel getal op te schuiven.
Nu is meteen duidelijk welke getallen een goede benadering met noemer n hebben: die liggen in de intervalletjes van de vorm (k/n-1/n2,k/n+1/n2), met k=1,…,n-1, en in (0,1/n2) en (1-1/n2,1).
De totale lengte van die intervallen is gelijk aan 2/n (reken maar na).
Hiermee kun je voorspellingen doen: omdat 2/10+2/11+2/12+2/13+2/14+2/15 kleiner is dan 1 zijn er getallen zonder goede benadering met noemers 10 tot en met 15.
Noem de vereniging van de intervalletjes hierboven even An. Met behulp van de Categoriestelling van Baire kun je bewijzen dat er een relatief `dikke’ deelverzameling van het interval (0,1) is waarvan elk element tot oneindig veel van de An behoort en dus oneindig veel goede benaderingen heeft.
Dit nu is de aard van de stelling van Dimitris Koukoulopoulos en James Maynard: deze geeft, bij bepaalde definities van `goede benadering’, voorwaarden onder welke de verzameling getallen met oneindig veel goede benaderingen heel `dik’ is of juist heel `dun’, waarbij `dik’ en `dun’ ondubbelzinnige definities hebben. Daarnaast geeft de stelling ook een dichotomie: `dik’ en `dun’ zijn de enige mogelijkheden. Het is nooit zo dat ongeveer de helft van de getallen oneindig veel goede benaderingen hebben; de kans is altijd gelijk aan nul (wat niet betekent dat er geen getallen zonder oneindig veel goede benaderingen zijn) of gelijk aan één.
In het krantenartikel wordt nog het volgende voorbeeld van `mooie’ benaderingen gegeven: als hierboven moet |α-p/q| kleiner zijn dan 1/q2, maar q moet zelf ook een kwadraat zijn. In dat geval is de kans op oneindig veel mooie benaderingen gelijk aan nul, maar de bovengenoemde stelling van Baire garandeert toch dat er heel veel irrationale getallen met oneindig veel goede benaderingen zijn.
Ten slotte: voor de definitie van `goed’ waar dit stuk mee begon geldt dat <emelk irrationaal getal oneindig veel goede benaderingen heeft. Dat bewijs je niet met de methoden die hier beschreven zijn, daar moet je wat dieper de getaltheorie in duiken. Zie hiervoor de Wikipediapagina’s over Benaderingsstelling van Dirichlet en over Kettingbreuken.

Recent Comments