Posts in category meetkunde
Een vierkante seconde
Een tip voor een niet-standaard uitstapje in Delft: ga een vierkante seconde bekijken.
Delft heeft een mooie binnenstad maar in de buitenwijken kun je ook aardige dingen zien. Neem tram 1 richting Tanthof, stap uit bij de halte Van der Slootsingel, loop de straat met die naam helemaal uit en ga dan rechtsaf het park Buitenhof in. Op een zacht glooiende helling ligt het, een kunstwerk met de naam Een Vierkante Seconde. Je moet echt de helling op want anders zie je de stenen die het vierkant vormen niet.
Waarom `vierkante seconde’?
Als je nauwkeurig wil aangeven waar je bent dan geef je je coördinaten door met behulp van het systeem dat daar al een paar eeuwen voor gebruikt wordt: lengte- en breedtegraden. Op de aarde zijn (denkbeeldig) twee stelsels lijnen getrokken: van de noord- naar de zuidpool (meridianen), en loodrecht daarop, evenwijdig aan de evenaar dus (parallellen).
De meridiaan die door the Royal Observatory in Greenwich loopt heet de nulmeridiaan; samen met de evenaar vormt hij een soort assenkruis, met de evenaar als x-as en de nulmeridiaan als y-as.
Het snijpunt van de nulmeridiaan en de evenaar is de oorsprong. In plaats van x- en y-coördinaten spreken we van, respectievelijk, lengte en breedte en in plaats van positief of negatief zeggen we ooster- en westerlengte, en noorder- en zuiderbreedte.
De eenheid die gekozen is om lengte en breedte uit te drukken is de graad; dat is natuurlijk omdat alle lijnen (delen van) cirkels zijn. Dat is ook handig omdat de parallellen niet allemaal evan lang zijn: de `parallel’, bijvoorbeeld, aan de noordpool bestaat uit maar één punt.
Beide assen zijn in graden verdeeld. De evenaar in twee keer 180 graden: west en oost, als je de nulmeridiaan doortrekt krijgt je de meridiaan op 180° west en oost. De nulmeridiaan is in twee keer 90° verdeeld, noord en zuid.
Nu is nulmeridiaan van de evenaar tot de noordpool 10.000 km lang (per definitie) en dus is één graad ongeveer 111 km lang. Dat is nog vrij veel en daarom zijn de graden weer in 60 mminuten verdeeld, die 60 is een overblijfsel van de 60-tallige schrijfwijze voor getallen uit het oude Babylon. Een minuut langs de nulmeridiaan is ongeveer 1850 m lang; en dat is nu net de definitie van een zeemijl.
De minuten zijn zelf weer in 60 seconden verdeeld en een seconde langs de nulmeridiaan is dus zo’n 30 m lang.
Langs de parallellen worden de graden, minuten en seconden steeds korter. Als je in Park Buitenhof aankomt en het kunstwerk bekijkt zul je zien dat het er niet als een vierkant van 30 bij 30 meter uitziet. Je kunt aan het kunstwerk Geografische Plaatsbepaling Delft (dat is de officiële naam) zien hoeveel korter een seconde op onze breedte geworden is. Het kunstwerk is namelijk een vierhoek die door twee parallellen en door twee meridianen begrensd is.
Op de foto’s van de vier hoeken kun je zien welke lijnen dat zijn:
- de meridianen op
- 04° 20′ 07” O. L. en
- 04° 20′ 08” O. L.,
- en de parallelen op
- 51° 59′ 29” N. B. en
- 51° 59′ 30” N. B.
Ik ben de hele vierhoek rondgelopen; in de noord-zuidrichting had ik dertig stappen nodig en in de oost-westrichting maar negentien.
 |
 |
 |
 |
Voor de wiskundigen: Welke functie bepaalt de lengte van een seconde langs een parallel? Kloppen mijn gemeten lengten ongeveer?
Andere zaken
In het blad Pythagoras is ook al eens een stukje over de vierkante seconde verschenen. Naar aanleiding hiervan ontdekte ik dat je op moet passen als je met een GPS-apparaat in de hand op zoek gaat naar het kunstwerk. Toen de vierhoek werd gelegd (1970) gebruikte men in Nederland het systeem ED50, sindsdien is het systeem WSG 84 in gebruik genomen. Het verschil tussen die systemen is ongeveer 100 meter; met een apparaat dat op WSG 84 is ingesteld loop je het risico in een van de sloten rond het park terecht te komen. In dit document kun je meer lezen over het omrekenen tussen de twee systemen.
In een video van Ionica Smeets over de vierkante seconde wordt hier voor gewaarschuwd. Naar aanleiding van die video is er een Geocache bij het kunstwerk gemaakt.
Op de Kunstwachtwebsite kun je ook over Geografische Plaatsbepaling lezen. En op de website van een van de makers, Nelis Oosterwijk, kun je wat ontwerpschetsen zien.
En tau rund jorden, I
Dette er første delen av en oversettelse av en art ikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger).
Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen?
Fast alle har hørt om følgende oppgaven. Vi tar en tau og strekker den rund jorden, langs polene, slik at den sitter tett. På Nordpolen spleiser vi inn en ekstra meter tau. Så drar vi, og mange folk rund jorden, tauen opp slik at den er overalt like høyt over jordoverflaten; den blir en sirkel igjen. Hvor høyt kommer den til å bli? Kan en mus komme seg under tauen?
Svaret, tauen skal være overalt 16 centimeter høyt, blir en overraskelse for mange folk. inntil du utfører beregningen. Vi begynner med en tau som er 2πR lang, der R er jordens radius. Oppgaven er å bestemme radiusen til sirkelen som er en meter lengre. Det vil si: bestem R’ slik at 2πR’=2πR+1. Men det er lett å gjøre: divider med 2π, så får vi R’=R+1/(2π)≈R+0.159.
Beregninger viser at verdien av R er ikke viktig: hvis du forlenger en sirkel med en meter så forlenger du radiusen med nesten 16 centimeter.
Vi henger jorden på en spiker
Men hva om vi drar opp tauen bare på Nordpolen til den er helt stramm igjen? Som om vi skule bruke tauen til å henge jorden på en spiker. Hvor høyt kommer spikeren til å bli over Nordpolen? Kan en isbjørn komme seg under tauen?
Her er en tegning som viser hva vi prøver å gjøre.
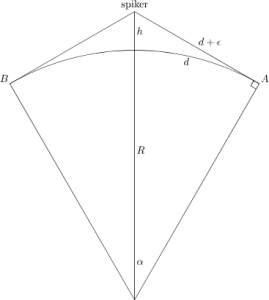
Det er lit enklere med bokstaver: R er jordens radius, ε er halvparten av tauen vi spleiset inn (en halv meter altså) og h er svaret på spørsmålet.
Buen d viser distansen fra Nordpolen til begge punktene der tauen sist berører jorden.
Vi har en rett vinkel i A (og B) fordi linjen fra A til spikeren er en
tangent til sirkelen. Nå kan vi finne en formel for h.
Vi begynner med Pythagoras sin læresetning:
![]()
og så h+R=±√(R2+(d+ε)2), eller
![]()
Dersom h er positiv må vi ta plussen, og
![]()
Vi tar R utenfor parentesen og får
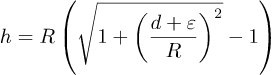
Det vi ikke vet her er verdien til d. Vi bruker radianer, og derfor d=αR eller α=d/R fordi, som vi skal se, det er enklere å lage en ligning for α.
Fra bildet ser vi hva tangensen til vinkelen α er:
![]()
og derfor
![]()
eller
![]()
Så, vår α er en løsning på siste ligningen.
Nå trenger vi noen tall. Jordens omkrets er, per definisjon, 40.000 km
(se illustrasjonen her). Derfor R=40.000.000/(2π) m og, selffølgelig, ε=½ m. Det betyr at vi må løse
![]()
Det finnes ingen enkelt formel for løsningen; det beste vi gjøre er å løse ligningen numerisk. De fleste grafiske kalkulatorene kan gjøre det for deg og jeg fikk denne løsningen: alpha;≈0.006176=6.176×10-3 og det betyr at d≈247.040 km. Det er interessant å vite hvor langt fra Nordpolen tauen forlater jorden men vi trenger ikke d i beregningene våre: vi setter α for d/R in formelen for h:
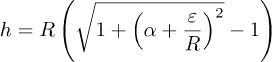
Når vi taster alle tallene in kalkulatoren får vi h≈121.4 m.
Oppgave
Gjør alt igjen men nå spleiser du inn bare en centimeter tau. Hvis tauen er lett nok kan du dra den stramm uten hjelp?
Selv om vi ikke har en eksakt formel for h som involverer ε og R kan vi noe om relasjonen mellom de tre størrelsene. Jeg skal skrive noe om det senere, in andere delen av denne historien.
Servetringen en Cavalieri
In haar laatste column voor de vakantie gaf Ionica Smeets de lezers een puzzel van Martin Gardner mee. Dit stukje gaat over een aspect van de puzzel dat in de column een beetje onbelicht blijft maar dat wel de sleutel tot een oplossing `uit-het-hoofd’ is.
Het probleem gaat als volgt: neem een bol en boor daar een cilindrisch gat in en wel zo dat je een servetring overhoudt die 6 cm dik is. Vraag: wat is het volume van die servetring. NB de as van de cilinder gaat door het middelpunt van de bol; de servetring is dus echt een ring.
Je kunt dat volume op een paar manieren bepalen. Leerlingen die wiskunde B hebben gedaan weten hoe ze volumes van wentellichamen met behulp van integralen uit kunnen rekenen. Als je toevallig wat formules voor volumes van bepaalde delen van een bol paraat hebt reken je het ook zo uit. Wat opvalt als je zo’n weg volgt is dat de straal van de bol er kennelijk niet toe doet. Dit is waarom Ionica dit een krankzinnig raadsel noemt: het lijkt of er een gegeven ontbreekt, namelijk de straal van de bol, maar achteraf blijkt dat niet zo te zijn. Dat had je dan op het spoor van een oplossing `uit-het-hoofd’ kunnen zetten: in de vraag wordt de straal niet genoemd, dan doe die er kennelijk niet toe, maar dan kan ik ook een heel makkelijk geval bekijken.
Maar goed, waarom doet die straal er niet toe?
De leerlingen die het volume met behulp van integralen gaan uitrekenen zien het meteen: in de integraal die uitgerekend moet worden is de straal van de bol verdwenen (hij komt twee keer in het kwadraat voor, maar die kwadraten worden van elkaar afgetrokken).
En wat doet iemand die niet kan integreren? Die gebruikt iets dat teruggaat tot Archimedes maar dat tegenwoordig bekend staat als het principe van Cavalieri.
Leg zo’n servetring op de grond en doe alsof het middelpunt van de bol op hoogte 0 ligt (zie het plaatje in de column). Snij nu de servetring met een wiskundige kaasschaaf in flinterdunne plakken. Bekijk de ringvormige plak op hoogte z. Die ring heeft een buitenstraal en een binnenstraal. De buitenstraal is gelijk aan √(R2-z2) en de binnenstraal is gelijk aan de straal van de cilinder en die is gelijk aan √(R2-32). De oppervlakte van de ring is dan gelijk aan π(R2-z2-R2+32) ofwel π(32-z2) en dat is onafhankelijk van de straal van de bol.
Het principe van Cavalieri zegt, toegespitst op dit geval: als je twee lichamen hebt van gelijke hoogte en op elke hoogte zijn de oppervlakten van de horizontale plakken uit de lichamen even groot dan zijn de volumes van de lichamen aan elkaar gelijk.
En daarom kun je volstaan met het probleem in een heel speciaal geval op te lossen.
Bijna twintig jaar geleden stond in Pythagoras een stukje over de manier waarop Cavalieri zijn principe gebruikte om oppervlakten te bepalen.
Het klinkt wel mooi dat principe van Cavalieri maar klopt het eigenlijk wel? Hoe zou je het bewijzen? Dan komen we vanzelf uit op de vraag wat `volume’ eigenlijk betekent. Na veel nadenken is daar een werkbare definitie van gegeven en gaat het bewijs van het principe via de integraal die de wiskunde-B-ers voor de oplossing van Gardner’s probleem zouden kunnen gebruiken.
Bruggen bouwen
In het Noorse radioprogramma Abels Tårn werd op 23 maart een poging gedaan uit te leggen waarom Robert Langlands de Abelprijs 2018 had gekregen. “Hij bouwde bruggen tussen diverse gebieden in de Wiskunde.” Veel verder ging de discussie niet; al viel de kreet `Automorfe Vormen’ nog even.
Voor wie wil weten wat het Langlands Program inhoudt kan op op de website van de Abelprijs wat inleidende artikelen vinden. In het radioprogramma werd nog even verwezen naar een eerdere winnaar Andrew Wiles. Diens bewijs van de Grote Stelling van Fermat is een voorbeeld van het gebruik van zo’n brug tussen Getaltheorie aan de ene oever en Algebraïsche Meetkunde aan de andere.
Ik vroeg me af of er niet een klein bruggetje tussen getaltheorie en meetkunde (algebraïsch of anderszins) bestaat dat als illustratie kan dienen.
Misschien helpt dit, een eenvoudige getaltheoretische vraag: bestaan er twee kwadraten (van natuurlijke getallen) waarvan de ene het dubbele van de andere is? Dat wil zeggen: zijn er twee natuurlijke getallen, m en n, zo dat n2=2×m2?
Je kunt voor dit probleem een brug naar de meetkunde slaan: teken twee vierkanten, een van n bij n en een van m bij m. De vraag is of je m en n zo kunt kiezen dat de oppervlakte van het eerste vierkant twee keer zo groot is als het tweede.
In de meetkundige versie kun je de vierkanten als hieronder tekenen.
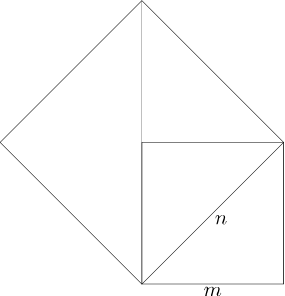
Om een gegeven vierkant in oppervlakte te verdubbelen moet je een vierkant tekenen waarvan de zijden gelijk zijn aan de diagonaal van het eerste vierkant.
Neem nu de rechthoekige driehoek met zijden m, m en n. Pas m af op de schuine zijde en teken de lijn vanuit z loodrecht op de schuine zijde naar de basis.

De schuine zijde van de nieuwe driehoek is de diagonaal van een vierkant met zijden n-m en dus geldt dat het kwadraat van die zijde gelijk is aan 2(n-m)2. Schrijf dat uit en gebruik dat n2=2m2:
2(n-m)2=2n2-4nm+2m2=4m2-4nm+n2=(2m-n)2
Dus die schuine zijde is inderdaad 2m-n lang.
Dit laat zien dat het niet mogelijk is natuurlijke getallen m en n te vinden als gewenst: als er twee van die getallen zijn dan kun je twee andere vinden die kleiner zijn. Maar in de natuurlijke getallen geldt: als er een getal met een bepaalde eigenschap bestaat dan is er ook een kleinste getal met die eigenschap. We hadden dus onze m en n zó kunnen kiezen dat n het kleinste getal is waarvoor een m bestaat met n2=2m2 en dan is 2m-n een echt kleiner getal met dezelfde eigenschap. Die tegenspraak laat zien dat zo’n n er in het geheel niet is.
Dus, als in het bewijs van Wiles, heeft de meetkunde geholpen bij het oplossen van een getaltheoretisch probleem.
Overigens heeft het getaltheoretische probleem een eenvoudige getaltheoretische oplossing: in een kwadraat n2 komt de priemfactor 2 een even aantal malen voor, namelijk twee keer zo vaak als in n zelf. En in het dubbele van een kwadraat, 2m2 komt 2 een oneven aantal malen voor: een even aantal maal in m2 plus de ene extra factor 2. Dus 2m2
is nooit gelijk aan n2.
En vele mensen hopen dat de grote stelling van Fermat ook zo’n eenvoudig bewijs heeft.
KP zag een gat
Op twitter raakte ik betrokken in een discussie over gaten, in het bijzonder over het aantal gaten dat een rietje heeft. Het antwoord hangt natuurlijk af van wat je als `gat’ aanmerkt maar als je er wiskundigen (in dit geval Ionica Smeets en mij) bij haalt dan krijgt je `één’ als antwoord. En dat komt omdat wiskundigen precies hebben afgesproken wat een `gat’ is en die afspraak leidt tot dat antwoord.
Wat is een gat dan?
We (de wiskundigen dan) beschouwen het rietje als een oppervlak en we tellen de gaten in dat oppervlak door vanuit een vast punt op dat oppervlak krommen te tekenen die beginnen en eindigen in dat punt. Dat is wat lastig met een fysiek rietje dus nemen we een rietje van een heel elastisch materiaal en door het aan één kant op te rekken kun je er een ringvormig gebied in het platte vlak van maken. Het tekenen gaat daar wat makkelijker; je kunt de krommen met touwtjes of elastiekjes maken; dat scheelt uitgummen als het papier te vol wordt.
Bij sommige krommen kun je het elastiekje laten krimpen tot het zo klein is als het vaste punt en zonder dat het elastiekje buiten het werkgebied komt. Bij andere lukt dat niet, bijvoorbeeld één keer (tegen de klok in) om het binnengebied gaat (of twee keer, of drie keer, …).
Een kromme die niet tot het vaste punt samengetrokken kan worden zonder buiten het werkgebied te komen wijst, wiskundig gesproken, op een gat. Dit betekent niet dat we vinden dat er oneindig veel gaten in het gebied zitten. Je kunt namelijk bewijzen (en dat kost enig werk) dat elke kromme (elastiekje) vervormd kan worden tot die ene kromme die één keer linksom het binnengebied gaat; daarbij wordt het aantal keren dat de kromme om het binnengebied gaat bewaard.
Dus een kromme die drie keer om het binnengebied gaat kun je vervormen tot drie keer achtereen die ene kromme, met behoud van richting.
Omdat elke kromme eigenlijk een aantal keer de ene basiskromme doorloopt vinden we dat het gebied één gat heeft.
Een T-stuk
Verderop in de twitterlijn kwam dit plaatje tevoorschijn: een bouwsel van twee rietjes dat eigenlijk een T-stuk voorstelde. Nu heeft een T-stuk drie openingen maar wiskundig gesproken zijn er maar twee gaten. Dat is met de nieuwe grens van 280 karakters net in één tweet uit te leggen:
Buig gaten 1 en 3 naar links zo dat je een broek krijgt; krimp de pijpen in tot je een zwembroekje overhoudt. Leg het broekje op tafel waarbij je gat 2 onder houdt en zover oprekt dat het de buitenrand wordt. Strijk alles glad: cirkelschijf met twee gaten.

Er zijn nu twee basiskrommen: neem een punt ergens in het midden en teken een kromme die één keer om het linkergat gaat en één keer om het rechtergat (beide tegen de klok in).
Elke andere kromme die in het gekozen punt begint en eindigt is te vervormen tot eentje die de basiskrommen doorloopt. Hierbij is het wat ingewikkelder dan bij één gat. De volgorde is van belang: eerst links dan rechts is niet hetzelfde als eerst rechts dan links.
Dus: twee basiskrommen en daarmee twee gaten.
Gaten in de kaas
Gaten (bubbels) in de kaas kun je niet met krommen detecteren: je kunt elke kromme tot een punt vervormen buiten alle holtes om. In dat geval gebruikt men (virtuele) ballonnen: een ballon waar een gat binnen ligt kun je niet geheel binnen de kaas samentrekken. Je kunt zelfs `basisballonnen’ definiëren en laten zien dat elke andere ballon tot een combinatie van basisbalonnen te vervormen is maar dat afspreken is een stuk ingewikkelder dan bij het doorlopen van krommen.
Kwadratuur van de cirkel, II
Vorige keer hebben we bekeken wat `Kwadratuur van de Cirkel’ inhoudt in het kader van Euclidische Meetkunde. We hebben ook gezien dat kwadratuur van de cirkel niet mogelijk is met een passer en een latje. Deze keer gaan we bekijken of er andere manieren zijn om die kwadratuur uit te voeren.
Banach en Tarski
In het begin van de twintigste eeuw rees de behoefte om aan steeds meer deelverzamelingen van de getallenlijn, het vlak, en de ruimte respectievelijk een `lengte’, `oppervlakte’ of `volume’ toe te kennen. Om enige afstand tot de concrete meetkunde te bewaren begon men het woord `maat’ te gebruiken en de eerste die een goede definitie van `maat’ formuleerde was Lebesgue, in 1908.
Later is dit door anderen in zijn volle algemeenheid uitgewerkt maar in de bovengenoemde drie gevallen gebruiken we de Lebesgue-maat nog vrijwel zo als Lebesgue hem gedefinieerd heeft.
Voor bekende meetkundige figuren geeft de Lebesgue-maat de reeds bekende waarde maar voor willekeurige verzamelingen gaat het niet altijd even goed.
Een extreem voorbeeld hiervan werd gegeven door de Polen Banach en Tarski. Voortbouwend op werk van Hausdorff lieten ze zien dat men een massieve bol met straal 1 in eindig veel (vijf is genoeg) deelverzamelingen kan verdelen, en dat men daarna die eindig veel stukken in elkaar kan schuiven tot twee massieve bollen van straal 1. Wie met het artikel van Banch en Tarski in de hand nu een wonderbaarlijke vermenigvuldiging van één sinaasappel tot twee sinaasappels wil uitvoeren komt bedrogen uit.
De bollen zijn ideale wiskundige bollen, geen fysieke sinaasappels. En, en daar was het Banach en Tarski om te doen, de stukken waarin ze de bol verdeelden zijn zo lelijk dat er op geen enkele manier een maat aan toe te kennen is. Immers als dat wel mogelijk was dan zou 1+1=1 bewezen zijn.
Terug naar het vlak
De vraag is nu of de wonderbaarlijke vermenigvuldiging in het vlak ook mogelijk is. Dat bleek niet het geval. Als je een verzameling die een maat heeft in eindig veel deelverzamelingen verdeelt en als je die stukken, hoe lelijk ook, tot een andere verzameling in elkaar legt en die nieuwe verzameling heeft een maat dan zijn de maten van beide verzamelingen gelijk.
U voelt hem wellicht al aankomen: Tarski formuleerde een abstracte versie van `de kwadratuur van de cirkel’: kunnen we een cirkelschijf, zeg van oppervlakte 1, in eindig veel verzamelingen verdelen en die stukken weer in elkaar schuiven tot een vierkant van oppervlakte 1?
In 1990 beantwoordde Miklos Laczkovich deze vraag met “Ja”. De gebruikte stukken zijn vrij lelijk, maar ze hoeven alleen verschoven te worden, draaien hoeft niet. De kwadratuur van de cirkel is dus mogelijk, zij het met instrumenten die veel geavanceerder zijn dan een passer en een liniaal.
Iets over het woord `lelijk’. De ontdekkingen door Banach en Tarski en anderen van verzamelingen waaraan geen maat toe te kennen is leidden tot een vakgebied dat Beschrijvende Verzamelingenleer is gaan heten. Hierin worden verzamelingen geklassificeerd naar hun beschrijvingen; het `lelijk’ dat ik een paar keer gebruikt heb kan daar precies gemaakt worden: de verzamelingen van Banach en Tarski, en van Laczkowicz hebben, noodzakelijk, beschrijvingen die vele malen ingewikkelder zijn dan die van verzamelingen die je normaal tegenkomt als lijnen, krommen en andere herkenbare figuren.
En toch …
Aan het eind van 2016 kreeg dit verhaal nog een nieuw slot. Andrew Marks en Spencer Unger bewezen dat de kwadratuur van de cirkel met stukken gedaan kan worden die in de Beschrijvende Verzamelingenleer als zeer mooi zouden worden aangemerkt, de technische term is “van Borel-complexiteit ten hoogste vier”. Voor U naar de winkel holt om deze `heel mooie’ legpuzzel aan te schaffen: hoewel de stukken in het grote geheel van de deelverzamelingen van het vlak redelijk eenvoudig zijn, zijn ze nou ook weer niet zo makkelijk met de hand te maken en vast te pakken.
Daar komt nog bij dat er wel een heel grote doos nodig is om alle stukken in te bewaren: bij een lezing over dit resultaat werd Andrew Marks naar het aantal benodigde stukken gevraagd; zijn antwoord: in de orde van grootte van 10220. Dat is dus een Googol in het kwadraat, maal nog een keer 1020.
Verder lezen
Veel van wat hierboven is beschreven is uitgebreid na te lezen in The Banach-Tarski Paradox (second edition) van Grzegorz Tomkowicz en Stan Wagon uit 2016. Het resultaat van Marks en Unger is daar nog niet te vinden; `Borel circle-squaring’ is nog één van de grote open problemen in het boek. Wie zin heeft kan het artikel te pakken krijgen via arxiv.org.
Kwadratuur van de cirkel, I
`De kwadratuur van de cirkel’ is voor velen een metafoor voor onmogelijkheid en/of futiliteit; in het Engels is `circle-squarer’ een gangbare term voor iemand die iets onmogelijks voor elkaar probeert te krijgen.
Toch is het recentelijk gelukt: gegeven een cirkelschijf een vierkant maken met dezelfde oppervlakte, en wel door die schijf in een eindig aantal stukken te knippen, die op te schuiven en weer aan elkaar te leggen tot dat vierkant.
In de komende blogposts zal ik het verhaal van het probleem en de oplossing vertellen.
Lang geleden zag ik een cartoon waarop een passer te zien was die ‘s avonds op straat tegen een muur (of lantaarnpaal) geleund stond te dromen. In het droomballonnetje was een vierkant te zien. Ik heb die cartoon uitgeknipt en lang bewaard maar hij moet bij een verhuizing verloren zijn gegaan want ik kan hem niet meer vinden.
Nu kan je die cartoon op diverse niveaus waarderen maar voor mij was het een mooie illustratie bij een beroemd onmogelijkheidsbewijs uit de wiskunde: het is niet mogelijk met behulp van passer en liniaal bij een cirkelschijf met straal 1 een vierkant te maken met precies dezelfde oppervlakte als die schijf.
Euclides en Archimedes
Waarom `passer en liniaal’? Dat komt voort uit De Elementen van Euclides. Daarin wordt de Meetkunde opgebouwd vanuit een beperkt aantal uitgangspunten, waaronder de beroemde vijf postulaten. In de bewijzen worden alleen stappen gezet die in die postulaten beschreven zijn:
- Gegeven twee punten trek de lijn door die twee punten.
- Gegeven twee punten trek een cirkel door één van de punten en
met het andere punt als middelpunt.
Euclides formuleerde de eerste stap in twee postulaten: je kunt de twee punten verbinden met een lijnstuk en dat lijnstuk kun je willekeurig verlengen; in redeneringen is het wat makkelijker in één keer die (oneindig lange) lijn getekend te denken. Deze twee stappen kunnen uitgevoerd worden met een liniaal en een passer, vandaar `passer en liniaal’. Overigens heeft die liniaal geen schaalverdeling en daarom spreken sommige boeken, om verwarring te voorkomen, liever van `passer en latje’.
De boeken van De Elementen staan dus vol met constructies die niet meer gebruiken dan de bovengenoemde twee stappen. Onder meer ook constructies van
- een paralellogram met dezelfde oppervlakte als een gegeven driehoek
- een rechthoek met dezelfde oppervlakte als een gegeven rechtlijnige figuur
- een vierkant met dezelfde oppervlakte als een gegeven parallellogram
Het patroon lijkt me duidelijk: bij zoveel mogelijk figuren een vierkant maken met dezelfde oppervlakte. Dat is waar het woord `kwadratuur’ (wat ouder: `quadratuur’) vandaan komt: de oppervlakte van een figuur wordt bepaald geacht als er een vierkant met dezelfde oppervlakte is geconstrueerd.
Wat in De Elementen niet wordt gedaan is de oppervlakte van een cirkelschijf bepalen.
Iemand die wel iets over die oppervlakte kon zeggen was Archimedes. Die bewees dat de oppervlakte van een cirkelschijf met straal r gelijk is aan die van een driehoek met hoogte gelijk aan r en basis gelijk aan de omtrek van de cirkel.
Aangezien de omtrek van de cirkel gelijk is aan 2πr is de oppervlakte van de schijf dus gelijk aan ½×2πr×r en dat is gelijk aan het welbekende πr2. Archimedes had deze notaties nog niet tot zijn beschikking; hij moest het bij de bovengegeven formulering houden. Hij liet ook zien dat, in moderne termen, π tussen de twee rationale getallen 3+10/71 en 3+10/70 ligt.
De bewijzen zijn on-line te vinden via de wikipedia-pagina “Measurement of a Circle”.
Onmogelijkheid
In de negentiende eeuw werd duidelijk waarom die kwadratuur van de cirkel niet in De Elementen gegeven was. Het is namelijk niet mogelijk om dat met alleen passer en latje te doen.
De sleutel tot deze oplossing ligt in het invoeren van coördinaten in het
platte vlak en het kijken wat men algebraïsch kan zeggen over de coördinaten van de punten die construeerbaar zijn vanuit de punten (0,0) en (1,0).
Het blijkt dat we met passer en latje kunnen optellen, aftrekken, vermenigvuldigen, delen en vierkantswortels trekken. En dat is alles.
Op deze manier zijn veel getallen, zoals √2, √(√2), √(2+√(3+√5)), … te construcren, maar lang niet alle getallen. In het bijzonder zijn de getallen π en √π niet met passer en latje te construeren; dat werd door Lindemann in 1882 aangetoond: er is geen enkele manier om uitgaande van het getal 1 en met gebruik van optellen, aftrekken, vermenigvuldigen, delen en vierkantswortels het getal π te maken (en √π dus ook niet).
Volgende keer: als niet met passer en latje kan het op een andere manier wel? Het antwoord is ja, maar de constructie kost heel wat moeite.

Recent Comments