Posts in category Logica
Lariekoek? II
We gaan het artikel Sets and Sentences van D. Terrence Langendoen en Paul Postal opnieuw lezen. De vorige keer heb ik de inhoud beschreven; nu bekijken we die nogmaals, maar met een wiskundig oog.
Zoals vorige keer beschreven gaat het er in het artikel om te laten zien dat in een Natuurlijke Taal de mogelijke zinnen een zeer grote collectie vormen: te groot om `verzameling’ genoemd te mogen worden. We volgen de redenering stap voor stap.
De definitie van Co-ordinate compound constituent is vorige keer al schematisch weergegeven door het volgende plaatje:
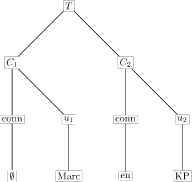
De top T is hier de co-ordinate compound constituent en de andere knopen zijn de conjucten waar T uit gevormd is. Die conjuncten bestaan uit een connectief en `constituent’. Ietwat simplistisch: T ontstaat door de constituents door middel van connectieven aan elkaar te plakken.
In punt (6) van het artikel wordt gedetailleerd beschreven hoe dat plakken in zijjn werk moet gaan, of preciezer: er wordt geformuleerd wat de relatie tussen de verzameling U van constituents en de compound T moet zijn. Uit die formulering zou je een plakmethode kunnen distilleren. Van punt (6) citeer ik deelpunt (d)
if two elements of U occur as subconjuncts of conjuncts C1 and C2 of T then C1 and C2 occur in a fixed order. Where C1 and C2 are of distinct length assume the shorter precedes; where C1 and C2 are the same length, assume some arbitrary order.
Als een student zoiets opschrijft trek ik mijn rode pen: ten eerste om het gebruik van `fixed’ en `arbitrary’ vlak achter elkaar, en ten tweede om dat `arbitrary’. Dat lees ik als “doe maar wat” en daar schrijf ik dus “Hoe dan?” bij. Ik kom straks nog op dit punt terug.
Verder in punt (6) wordt T een `co-ordinate projection’ van U genoemd en U de `projection set’ van U. Inderdaad: U is door T uniek bepaald maar niet andersom; het woord `arbitrary’ lijkt daar op te duiden.
Dan volgt een alinea waarin wordt beargumenteerd dat elke verzameling U een co-ordinate projection heeft. Dit zou `straightforward’ moeten zijn, volgens de schrijvers althans. Hier zijn de stappen (de `category Q’ die ter sprake komt is een niet nader gespecificeerde abstracte categorie van zinnen):
- Neem een verzameling U en laat k de kardinaliteit van U zijn (eindig of oneindig)
- Citaat:
Clearly, from the purely formal point of view, there is a co-ordinate compound W belonging to the category Q.
Dat klinkt mooi maar het heeft geen enkele bewijskracht; geen enkele rechtvaardiging, geen indicatie waar die W vandaan zou moeten komen. - Citaat:
Since there are no size restrictions on co-ordinate compounds, W can have any number, finite (more than one) or transfinite of immediate constituents.
Dit is slechte (wiskundige) stijl: eerst lijkt W vast, dan gaat hij alsnog variëren. Een betere formulering zou zijn: “er zijn co-ordinate compounds van alle mogelijke kardinaliteiten”. Die betere formulering maakt de bewering niet automatisch waar, er is nog steeds geen concrete rechtvaardiging gegeven. - Citaat:
W can then, in particular have exactly k such constituents.
Nogmaals: die vaste W is omgevormd tot een gepaste W. Niet mooi, maar vooruit dan maar. - De deelconjuncts van de conjuncts in W vormen een verzameling V die, volgens de regels in (6), kardinaliteit k heeft. Niks mis mee.
- Citaat:
To show that W is a co-ordinate projection of U, it then in effect suffices that there exist a one-to-one mapping from U to V.
Niet dus. Hoe je definitie (6) ook wendt of keert, dit haal je er niet uit. Wil W een co-ordinate projection van U zijn dan zal de verzameling V exact gelijk aan de verzameling U moeten zijn; een bijectieve afbeelding tussen die twee is echt niet genoeg. - Citaat:
But this is trivial, since the two sets have the same number of elements.
Dit klopt, maar ik verdenk de schrijvers ervan dat ze niet doorhebben wat hier achter zit. Georg Cantor definieerde `kardinaliteit’ op een manier die eigenlijk nietszeggend is, zie de tweede post in deze serie. Hij bewees daarna dat `hebben gelijke kardinaliteit’ equivalent is met `er bestaat een bijectieve afbeelding tussen’, maar tegenwoordig is dat laatste de definitie van het eerste.
Afsluiting
In het artikel formuleren Langendoen en Postal nu een afsluitingsprincipe. Na een waarschuwing dat niet elke co-ordinate projection noodzakelijkerwijs welgevormd is komt het volgende Closure Principle for Co-ordinate Compounding:
If U is a set of constituents each belonging to the collection, Sw, of (well-formed) constituents of category Q of any natural language, then Sw contains the co-ordinate projection of U.
Hoezo “the co-ordinate projection”? Uniciteit van die projecties is nog niet aan de orde geweest en over die collectie Sw is niet (expliciet) gezegd dat elke verzameling zinnen maar op één manier tot een grotere zin samen te voegen is.
Na een opmerking over het recursieve karakter van dit principe noemen de schrijvers de categorie S van zinnen als een categorie waarop het principe van toepassing is, althans: ze beweren dat (maar geven geen bewijs).
Dat weerhoudt ze er niet van het principe twee keer uit te spreken voor S. Eerst via een bijna letterlijke herhaling, met Q vervangen door S, en dan nog een keer met behulp van een formule(!): the co-ordinate projection van een verzameling U noteren we CP(U) en dan krijgen we
(∀U)(U⊂L → CP(U)∈L)
Hierin is L de collectie van alle elementen van de categorie S van een natuurlijke taal (voor mij betekent dat L=S want L en S hebben dezelfde elementen, maar er is misschien een subtiel verschil tussen de collectie van elementen van een categorie en de categorie zelf). Merk op dat hier het onbepaalde lidwoord definitief bepaald geworden is. Zonder het expliciet uit te spreken hebben de schrijvers kennelijk besloten dat compounding maar op één manier kan; de functienotatie CP(U) kan niet anders geïnterpreteerd worden.
Maar hoe is CP(U) gedefinieerd dan? Dat wordt niet duidelijk; een illustratie met met verzamelingen van drie, vier zinnen die tot één worden samengevoegd overtuigt mij niet.
Een soort van hierarchie
Dan komt eindelijk datgene waar ik al lang op zat te wachten: The Cantorian Analogue, waarin bewezen gaat worden dat de zinnen in een natuurlijke taal geen verzameling vormen. Overigens, een definitie van `verzameling’ hebben we nog niet echt gehad.
Het bewijs gaat aanvankelijk met gebruik van een verzameling zinnen als in de vorige post, de schrijvers gebruiken {Babar is happy; I know that Babar is happy; I know that I know that Babar is happy, …}. Die verzameling noemen ze S0.
Ik kort de zinnen even af: z0 is “Babar is happy” en, gegeven zn is zn+1 de zin “I know that zn“.
Onder de aanname dat de natuurlijke taal L aan het afsluitingsprincipe voldoet omvat L ook de verzameling S1 die bestaat uit S0 en de co-ordinate projections van de deelverzamelingen van S0 met twee of meer elementen. De formulering verdient het nauwkeurig gelezen te worden.
Then L also contains a set S1, made up of all the sentences of S0 together with all and only the co-ordinate projections of every subset of S0 with at least two elemente, that is, with a set containing one co-ordinate projection for each member of the power set of S0 whose cardinality is at least 2.
Deze zin deugt niet. De delen voor en na `that is’ spreken elkaar tegen. De eerste versie van S1 bevat alle co-ordinate projections van alle deelverzamelingen van S0 — de projecties van iedere deelverzameling —; de tweede versie bevat van elke deelverzameling (precies) één projectie. Daarnaast is de eerste versie uniek bepaald door het `all and only’, daar is `the set S1‘ dus meer op zijn plaats; in het tweede deel past `a set’ wel.
Je zou het meervoud `projections’ enkelvoud kunnen maken; dat sluit wat beter aan bij de formulering van de afsluitingeigenschap, the projection zou dan telkens de functiewaarde CP(U) kunnen zijn. Maar dan gaat het ook mis: vóór het `that is’ is de keuze van projectie duidelijk vastgelegd, maar na `that is’ zit er nog potentiële willekeur in de keuze van projectie, er staat niet expliciet dat die one projection ook echt CP(U) is.
De schrijvers geven dan een voorbeeld van hoe S1 er uit zou kunnen zien (dus toch geen welbepaalde verzameling):
{z0; z1; z2; …; z0 and z1; z0 and z2; …; z0, z1, and z2 …} (voor alle duidelijkheid: de punt-komma’s scheiden de zinnen en de komma’s dienen als connectieven in de zinnen).
Dan volgt een lange alinea waarin met veel omhaal van woorden de kardinaliteit van S1 wordt bepaald. Door het `één projectie per verzameling’ is dat niet moeilijk: dat is dezelfde kardinaliteit als die van de familie van alle deelverzamelingen van S0 en omdat S0 aftelbaar oneindig is, en dus kardinaliteit ℵ0 (alef-nul) heeft is die kardinaliteit gelijk aan 2ℵ0 (2-tot-de-macht-alef-nul) en niet ℵ1, zoals Langendoen en Postal opschrijven. Ergens bij hun bestudering van de verzamelingenleer is er iets misgegaan en is de Continuümhypothese waar geworden.
Zoals wellicht verwacht wordt dit proces voortgezet. Er komt een rij verzamelingen S0, S1, S2, …, netjes recursief gedefinieerd door Sn+1=Sn∪Kn. Hierbij is Kn telkens de verzameling projecties van deelverzamelingen van Sn. In formule
Kn={x:(∃y)(y⊆Sn ∧ x is the co-ordinate projection of y)}
Hier had dus ook Kn={x:(∃y)(y⊆Sn ∧ x=CP(y))} kunnen staan.
Op deze manier komt er een hierarchie van verzamelingen zinnen tot stand; die zinnen worden steeds complexer en de verzamelingen steeds groter. De schrijvers claimen onterecht dat voor elke n het kardinaalgetal van Sn gelijk is aan ℵn. De juiste formule is een machtsverheffing met een torentje van n tweeën, met bovenaan nog een ℵ0. Dat kardinaalgetal noteren we in de verzamelingenleer als ℶn (beth-n).
Dit verhaal culmineert in wat de schrijvers The NL Vastness Theorem noemen: Natural Languages are not sets.
Het bewijs verloopt uit het ongerijmde. Neem aan dat L een verzameling is. Het proces van co-ordinate projection definieert een injectieve afbeelding van de machtsverzameling van L naar L zelf. Dat kan niet volgens een stelling van Cantor: elke verzameling heeft strikt meer deelverzamelingen dan elementen. Tegenspraak.
Er is echter een groot MAAR, en daar gaan we het nu over hebben.
Ordeningen en lengten
Het `bewijs’ in het artikel staat vol met impliciete aannamen over het gedrag van verzamelingen die een niet-wiskundige waarschijnlijk niet zo snel zullen opvallen. Er zijn twee dingen die nogal schadelijk zijn voor de redenering zoals hierboven beschreven.
Ten eerste de ordening, ik heb er bij de beschrijving van de co-ordinate projection al op gezinspeeld: daar zit, op zijn zachtst gezegd, een onvolledigheid.
Die onvolledigheid duikt op bij de overgang van S1 naar S2, en nog erger bij de stap daarna van S2 naar S3.
Bij de eerste stap, van S0 naar S1, is er niets aan de hand: we hebben onze verzameling S0 genummerd en die nummering ordent elke deelverzameling van S0, waarmee zo’n deelverzameling een natuurlijke projectie heeft, ook als deze oneindig veel elementen heeft. Dit levert natuurlijk wel zinnen zonder einde op.
Daarna, van S1 naar S2, hebben we een probleem: er zijn (overaftelbaar) veel zinnen van oneindige lengte (allemaal even lang als de verzameling der natuurlijke getallen). Daar gaat het `fixed’ en `arbitrary’ van punt (6)(d) dus wringen. Hoe orden je zo’n verzameling zinnen? De heren Langendoen en Postal spreken zich daar niet over uit.
Gelukkig kunnen we hier de lexicografische ordening gebruiken: kijk naar het eerste teken (inclusief spaties) waar de zinnen verschillen en neem een besluit op basis van de ordening van de tekens. Zie ook de post Boekenplanken voor gevorderden waar een aspect van die ordening aan de orde komt dat hier de zaak ook compliceert: er zijn heel veel verzamelingen die de eigenschap hebben dat tussen elk tweetal zinnen oneindig veel zinnen staan en die ook geen eerste zin hebben. Als we die ordening gebruiken om projecties te maken dan krijgen we dus zinnen zonder begin, zonder einde, en met voegwoorden die gaan ten minste één kant niet zien wat ze verbinden.
Het kan nog erger. We kunnen de verzameling S2 opvatten als de familie van alle deelverzamelingen van de reële rechte R. En op die familie kan geen lineaire ordening gedefinieerd worden. Het sleutelbegrip is hier `definiëren’: er is geen formule die de familie deelverzamelingen van R zó sorteert dat elk tweetal verzamelingen vergelijkbaar is. De stap van S2 naar S3 kan eigenlijk niet genomen worden.
Ten tweede is er nog het begrip lengte van een zin. Cantor heeft een hele theorie van orde-typen (`lengten’) van lineair geordende verzamelingen ontwikkeld. Wat daar vooral opvalt is dat er veel onvergelijkbare orde-typen zijn. En die kom je ook tegen bij de stap van S2 naar S3: het voorsorteren op `lengte’ gaat dus ook al niet.
Welordeningen?
“Maar, er zijn toch welordeningen?”, hoor ik degenen die wat verzamelingenleer hebben bestudeerd opwerpen. Dat klopt, en we hebben ook nog Zermelo’s Welordeningsstelling, die zegt dat elke verzameling een welordening heeft. Bij een welordening zijn de elementen zo gesorteert dat elke deelverzameling (niet-leeg) een eerste element heeft. Welordeningen zijn ook nog onderling vergelijkbaar, dus die co-ordinate projections schrijf je zo op.
Inderdaad, maar die welordeningsstelling is equivalent met het Keuzeaxioma en daarmee hoogst niet-constructief. Zoals de verzameling S2 geen definieerbare lineaire ordening heeft heeft S1 geen definieerbare welordening.
Je kunt met welordeningen werken maar dan laat je de willekeur van het Keuzeaxioma binnen en daarmee ben elke zweem van een grammatica kwijt.
Ik weet niet of je dan nog van een natuurlijke taal kunt spreken.
Korte samenvatting
We zijn hier nog niet aan het einde van het artikel Sets and Sentences gekomen. Er gebeurt wiskundig niet veel nieuws meer en het derde deel beargumenteerd dat zo ongeveer alle theoriën over natuurlijke getallen uit de tijd van schrijven niet deug(d)en. De argumenten steunen op The NL Vastness Theorem.
In het bewijs van die stelling zitten gaten. En die gaten bestaan vooral uit ontbrekende definities en aannamen.
Zo wordt nergens echt vastgelegd wat een verzameling eigenlijk is; het dichtst bij een definitie komt men in het bewijs van de Vastness Theorem: het kenmerkende van een verzameling is dat deze een kardinaliteit, een `aantal elementen’, heeft. Dat is de omgekeerde wereld en ook niet echt nodig.
Cantor definieerde eerst `Menge’ en pas daarna `Machtigkeit’; naar moderne maatstaven hebben die definities weinig inhoud maar ze stuurden de intuïtie wel de goede kant op.
De manier waarop ik het `bewijs’ van de stelling heb opgeschreven laat zien dat die aanname over kardinaliteit vermeden kan worden; we hebben alleen goede afspraken over het hebben van meer, minder en evenveel elementen nodig en dat kan zonder die aantallen te definiëren of benoemen. Net als we geen eenheid van lengte nodig hebben om uit te maken of ik langer, korter, of even lang ben als Marc van Oostendorp: zet ons naast elkaar en je weet het.
Zoals al opgemerkt zijn de centrale noties van het artikel niet goed afgesproken; de definities lijken, gezien de gegeven voorbeelden, vooral ingegeven door de eindige situatie. Bij het suggestief opschrijven van de verzameling S1 zien we ook alleen maar eindige zinnen.
Ik vermoed dat niemand de schrijvers heeft gevraagd hoe men het zich moet voorstellen: een collectie zinnen die geordend is als de rationale getallen: zonder begin, zonder eind en met tussen elk tweetal zinnen ondindig veel andere. Hoe maak je daar een goedlopende zin van?
Loterijen? Eerder de Lotto.
Gisteren, in het stuk over bijna-disjuncte families, heb ik het niet over de loterijen gehad waar het in stuk in NewScientist over ging. Sommige mensen waren benieuwd naar die metafoor voor het resultaat in het artikel van David Schrittesser en Asger Törnquist. Ik doe hier een poging zo’n loterij te beschrijven. Ik laat het aan de lezer om te beoordelen welke uitleg beter is: de feitelijke in de vorige post of de metaforische hieronder.
Om te beginnen: `loterij’ is eigenlijk een verkeerde vertaling van het Amerikaanse `lottery’. Bij een loterij koop je een lot en weet je niet wat je lotnummer zal zijn. In een lottery kies je zelf de getallen op je kaartje. Het is dus eerder te vergelijken met onze Lotto. De beschrijving van de `loterij’ in NewScientist is ook eerder die van een variant op de Lotto dan op de Staatsloterij.
Een oneindige variant op de Lotto
In plaats van 6 uit 45 kiezen we getallen uit N. Met de betekenis van het woord `bijna’ van gisteren in gedachten leggen we vast dat we niet `bijna niets’ en ook niet `bijna alles’ mogen kiezen: we moeten er oneindig veel kiezen (aankruisen) en we moeten er oneindig veel niet aankruisen.
Een `formulier’ heeft dus oneindig lange kolommen (net zo lang als N) en oneindig veel kolommen. Je mag dus, kennelijk, oneindig veel kolommen invullen. Wat in het stuk niet duidelijk vermeld wordt is hoe je een prijs kunt winnen.
Maar met het artikel in de hand kunnen we wel wat regels opstellen. Het artikel bewijst namelijk dat oneindige maximale bijna-disjuncte families niet bestaan (dat `oneindige’ heb ik gisteren voor het gemak weggelaten maar dat wordt nu belangrijk); het stukje zegt dat er geen winnende formulieren bestaan. Conclusie: een (zeker) winnend formulier heeft in de kolommen een oneindige maximale bijna-disjuncte familie.
Daaruit concluderen we dan dat een winnende kolom een oneindige doorsnede heeft met de getrokken deelverzameling van N.
We halen hier ook nog wat voorwaarden uit waaraan een geldig formulier aan moet voldoen: niet alleen mag je in één kolom niet bijna alle getallen aankruisen, ook mag je er niet voor zorgen dat je over een eindig aantal kolommen bijna alle getallen aankruist. Als je bijvoorbeeld over tien kolommen achtereenvolgens de tienvouden, tienvouden-plus-1, … tienvouden-plus-9 aankruist win je ook zeker; die tien verzamelingen vormen een eindige maximale bijna-disjuncte familie.
Samengevat: op je formulier kruis je in een aantal kolommen telkens oneindig veel getallen aan. Dat aantal kolommen mag eindig zijn maar hoe dan ook: in elke eindige greep kolommen mag je nooit samen bijna alle getallen aankruisen. Je wint als je in ten minste één kolom oneindig veel getrokken getallen hebt aangekruist.
Door je kolommen bijna-disjunct in te vullen spreid je je inzet het zuinigst; twee kolommen met een oneindige doorsnede hebben een grote overlap aan mogelijkheden. Ten slotte: als je kolommen een maximale bijna-disjuncte familie vormen dan bevat je formulier, per definitie, een winnende kolom.
Het bestaan van (zuinige) winnende formulieren
Het stuk in NewScientist vertelt niet de hele waarheid. De suggestie wordt gewekt dat winnende formulieren niet bestaan. Dat is slechts voor de helft waar. Je kunt bewijzen dat zeker winnende en zuinige formulieren bestaan, met behulp van het Lemma van Zorn (een equivalent van het Keuzeaxioma).
Sommige wiskundigen vragen zich in dit soort situaties af of het Lemma van Zorn wel nodig is bij zo’n concrete vraag; dat Lemma levert namelijk nogal zwaar geschut. En dat is nu wat David Schrittesser en Asger Törnquist hebben vastgesteld: je hebt zwaar geschut nodig; er is bestaat een situatie waarin dat zware geschut niet voorhanden is en waarin geen enkele maximale bijna-disjuncte familie bestaat.
Loterijen? Nou, nee.
Vanochtend (2019-09-19) vond ik via twitter dit artikel uit NewScientist (een vrij letterlijke vertaling van dit stuk. Nadat ik het verhaal over niet-bestaande oneindige loterijen had gelezen was ik nog niets wijzer geworden. Na doorklikken naar het originele artikel zag ik dat ik het al eerder had gezien in april, op ArXiV.org en dat het niets met loterijen te maken had.
Maar waar gaat het artikel dan wel over? Over bijna-disjuncte families. En wat zijn dat nu weer?
Eén van mijn favoriete objecten in de verzamelingenleer is de familie van alle deelverzamelingen van de verzameling N der natuurlijke getallen. Dit is een nimmer opdrogende bron van vragen en resultaten die in veel delen van de wiskunde gebruikt worden maar die gewoon ook leuk zijn om aan te werken.
Hierbij is het bijwoord `bijna’ bijna niet te vermijden. In het artikel waar we het hier over hebben past men `bijna’ dus toe op `disjunct’. Nu noemen we twee verzamelingen A en B `disjunct’ als hun doorsnede leeg is, A∩B=∅, als er geen x is die zowel in A als in B zit.
Het woord `bijna’ kort eigenlijk het wat uitgebreidere `op eindig veel na’ af: twee verzamelingen zijn bijna disjunct als hun doorsnede eindig is — `hun doorsnede is op eindig veel elementen na leeg’. Hierbij eisen we wel dat de verzamelingen zelf oneindig zijn want anders is bijna-disjunctheid niet zo spannend.
De twee verzamelingen E en O van respectievelijk de even en oneven getallen zijn disjunct; er is geen natuurlijk getal van tegelijk even en oneven is.
Hier is een mooie truc, van Sierpinski uit 1928: voor elk positief irrationaal getal x en voor elk natuurlijk getal n doen we het volgende: bepaal n×x, neem het gehele deel [n×x] (gooi alles achter de komma weg) en deel dat weer door n.
Bij vaste x krijg je zo een rij rationale getallen: [x], [2x]/2, [3x]/3, [4x]/4, … Bij π bijvoorbeeld krijgen we zo 3, 3, 3, 3, 3, 3, 3, 25/8, 28/9, 31/10, 34/11, 37/12, …
Uit de definitie van de rij volgt dat 0<x-[n×x]/n<1/n voor alle n en dit betekent iets voor de bijbehorende verzamelingen termen. Bij elke x stoppen we de termen van de rij in de verzameling Sx, dus Sπ={3, 25/8, 28/9, 31/10, 34/11, 37/12, …}.
Neem nu eens twee irrationale getallen x en y met x<y; dan geldt voor n>1/(y-x) dat [n×y]/n>y-1/n>x, en dus zit [n×y]/n niet in Sx. We concluderen dat de verzamelingen Sx en Sy bijna disjunct zijn.
De verzamelingen Sx vormen het soort familie waar het artikel over gaat: een bijna-disjuncte familie, elk tweetal elementen is bijna disjunct (en elke Sx heeft oneindig veel elementen).
Het voorbeeld van Sierpinski laat zien dat er een groot verschil is tussen `disjunct’ en `bijna disjunct’. Als een familie disjunct is dan zit elk punt in ten hoogste één element van de familie. De bijna-disjuncte familie van Sierpinski bestaat uit verzamelingen rationale getallen, daar zijn er evenveel van als natuurlijke getallen. De familie zelf heeft evenveel elementen als er positieve irrationale getallen en dat zijn er veel en veel meer als er natuurlijke getallen zijn (en dat is allemaal precies te maken). Dat zorgt er voor dat veel van de rationale getallen in meer dan één verzameling Sx zitten.
Maar goed, terug naar het artikel. Het hoofdresultaat zegt iets over de aard van bijna-disjuncte families deelverzamelingen van N: onder bepaalde omstandigheden is er geen maximale bijna-disjuncte familie. Als je zo’n familie hebt kun je er een oneindige deelverzameling van N bij doen zó dat de grotere familie ook bijna-disjunct is (en nog één, en nog één, …).
Wat dit nou met loterijen te maken heeft? Ik zou willen zeggen dat ik geen idee heb maar dat heb ik wel. Ik vind de vergelijking echter zó vergezocht dat ik de lezer er niet mee lastig wil vallen. En ik denk eigenlijk dat de uitleg van die vergelijking lastiger is dan die van het resultaat zelf.
Machine Learning and the Continuum Hypothesis
Not even Machine Learning is safe from Set Theory, or so it seems. On the website of the journal Nature there is an article about a paper in Nature Machine Intelligence that connects a certain kind of learnability to the Continuum Hypothesis. The conclusion of the paper is that certain abstract learnability questions are undecidable on the basis of the normal ZFC axioms of Set Theory.
The article tries to explain what is going on but seems to confuse two disparate things: Gödel’s (First) Incompleteness Theorem on the one hand and the undecidability of the Continuum Hypothesis on the other hand.
The first is a very general statement about first-order theories; it states that for every theory that satisfies a number of technical conditions there are statements that have no formal proof and neither do their negations. Elementary number theory is subject to this theorem, as is ZFC Set Theory.
The second is a Set-theoretical statement for which we can prove that there is no formal proof, nor for its negation. It is also more interesting than Gödel’s statements; the latter `simply’ assert their own unprovability, whereas the Continuum Hypothesis is a fundamental statement/question about the set of real numbers.
The confusion manifests itself when the Continuum Hypothesis is called a paradox. It is not. The statements from the Incompleteness Theorem on the other hand are usually likened to the Liar Paradox in that “This formula if unprovable” looks a lot like the paradox that is “This sentence is false”.
The paper itself also alludes to the Incompleteness Theorem; it even states that is used in the argument. It is not. No use is made of Gödel’s abstract unprovable sentences.
The Set Theory
So, what is the Set Theory in the paper? The learnability question is shown to be equivalent to the existence of a natural number m and a map η from the family of m-element subsets of [0,1] to the family F of finite subsets of [0,1] that satisfies the following condition: if A is a subset of [0,1] with m+1 elements then it has a subset B with m elements such that η(B) contains A.
The main theorem of the paper states that an arbitrary set X admits such a map with m=k+1 if and only if X has cardinality at most ℵk.
If the Continuum Hypothesis holds then [0,1] has cardinality ℵ1, hence there is a map as required with m=2. More generally there is a map as required if the cardinality of [0,1] is equal to ℵk for some natural number k. These possibilities do not lead to contradictions, hence neither does the learnability statement. On the other hand, the statement that the cardinality of [0,1] is larger than all these ℵk does not lead to contradictions either, hence neither does the negation of the learnability statement.
The derivation of the main statement parallells that of the main result of the paper Sur une caractérisation des alephs by Kuratowski from 1951: a set X has cardinality at most ℵk if and only if its power Xk+2 can be written as the union of k+2 sets A1, …, Ak+2 such that for every i and every point (x1,…,xk+2) in the power the set of points y in Ai that satisfy yj=xj for j≠i is finite; in Kuratowski’s words “Ai is finite in the direction of the ith axis”.
Indeed one can even construct of a map η for m=k+1 from this decomposition of the canonical set ωk of cardinality ℵk.
For notational simplicity we take k=2, so m=3, and ω24 has a decomposition into four sets A1, A2, A3, and A4. Given a subset F of ω2 of 3 elements enumerate it in increasing order: x1<x2<x3. The set η(F) will consist of F itself together with
- all x for which (x,x1,x2,x3) belongs to A1,
- all x for which (x1,x,x2,x3) belongs to A2,
- all x for which (x1,x2,x,x3) belongs to A3,
- all x for which (x1,x2,x3,x) belongs to A4
To see that this works let G be a four-element subset of ω2, enumerate it as y1<y2<y3<y4. Then (y1,y2,y3,y4) belongs to one of the four sets, say it belongs to A2; then G is a subset of η({y1,y3,y4}): the point y2 is included in the second line in the list above.
Note. The proof of the main theorem (Theorem 1) of the paper is not quite correct: it fails for k=1 for example as one encounters the cardinal number ℵ-1. Worse: in that case the ordering <1 seems to have order type ω1 and ω0 simultaneously. All this can be repaired with a better write-up.
Het Compactheidsbeginsel
Twee recente artikelen op Kennislink hebben iets gemeen. Dat gemeenschappelijke is een belangrijk stuk gereedschap uit de Wiskunde dat bekend staat als het Compactheidsbeginsel.
In 2016 werd een kleuringsprobleem voor de natuurlijke getallen opgelost: is het mogelijk de natuurlijke getallen in tweeën te delen op zo’n manier dat beide delen geen enkel Pythagoreïsch drietal bevatten? Het antwoord is: “nee”. Zoals op Kennislink te lezen is is er iets meer ontdekt: bij elke verdeling van {1,2,3,…7825} in twee delen moet een van de delen een Pythagoreïsch drietal bevatten en er is een verdeling van {1,2,3,…,7824} waarbij geen van de beide delen een bevat.
Voor de goede orde: een Pythagoreïsch drietal is een drietal natuurlijke getallen (a,b,c) dat voldoet aan a2+b2=c2. Ook wordt het probleem vaak in termen van kleuringen geformuleerd: de verdeling wordt weergegeven door elk natuurlijk getal rood of blauw te kleuren.
Begin van deze maand werd vooruitgang geboekt bij een kleuringsprobleem in het platte vlak: in hoeveel verzamelingen moet je de punten in het vlak minimaal verdelen opdat geen enkel deel twee punten bevat die afstand 1 hebben. Er was lang bekend dat dat minimale aantal ten minste 4 en ten hoogste 7 is; nu is bekend dat het ten minste 5 moet zijn. Okk hier is al aan een eindige verzameling punten te zien dat bij elke verdeling in vier stukken er altijd een stuk is dat twee punten met afstand 1 bevat.
Waarom is dat? Het zou toch bij het eerste probleem zo kunnen zijn dat bij verschillende kleuringen de drietallen één kleur krijgen steeds hoger in de natuurlijke getallen moeten zitten. Maar kennelijk is het zo dat, ongeacht de kleuring er al een éénkleurig drietal is in {1,2,3,…,7825}.
Het geheim is een stelling van De Bruijn en Erdös; deze zegt dat bij elk kleurings probleem het volgende geldt: als elke eindige verzameling een `goede’ kleuring heeft dan is er een `goede’ kleuring voor de hele verzameling. Dat kun je ook als volgt contrapositief formuleren: als elke kleuring van de hele verzameling `slecht’ is dan is er een vaste eindige verzameling waarvoor elke kleuring `slecht’ is. In April 2014 is over deze stelling een artikel in Pythagoras verschenen.
Het voordeel van dit Compactheidsbeginsel is dat men voor positieve resultaten alleen naar eindige verzamelingen hoeft te kijken; dat kan de bewijzen aanzienlijk vereenvoudigen. Het nadeel is dat het niet constructief is: het geeft geen enkele informatie over de grootte van de vaste eindige verzameling waarvoor elke kleuring `slecht’ is. Dat laatste is te zien aan de resultaten waarover op Kennislink bericht werd; de zoektochten naar de eindige verzamelingen en de verificaties dat ze werkten kostten veel tijd en moeite.
Voegwoorden en rekenen
“Taal is geen Wiskunde” schreef @onzetaal als reactie op de vorige post. Inderdaad.
In 2002 stond in het tijdschrift Onze Taal een artikel Alle Aaanwezigen Behalve De Kinderen waarin de werking van voegwoorden gerelateerd werd aan, vooral, optellen en aftrekken.
En, helaas, na een bladzijde voorbeelden gaat het meteen mis:
De betekenis van en is gemakkelijk: het komt overeen met de optelling van twee aantallen. In de wiskundige verzamelingenleer worden aantallen als verzamelingen voorgesteld. De betekenis van `Jan is bakker en visser’ wordt in verzamelingstheoretische termen opgevat als `Jan behoort zowel tot de verzameling bakkers als tot de verzameling vissers.’
De betekenis van en is een stuk ingewikkelder dan optellen en dat laat het geciteerde voorbeeld meteen zien: door te zeggen `Jan is bakker en visser’ verwijst men inderdaad naar de doorsnede van twee verzamelingen: Jan∊Bakkers∩Vissers. Echter `Willen alle bakkers en vissers naar voren komen’ verwijst naar een vereniging: Bakkers∪Vissers. En beide mogelijkheden komen niet overeen met optellen: in het eerste geval laten we niet-vissers weg uit de verzameling bakkers en in het tweede geval is het totale aantal mensen niet noodzakelijk de som van de aantallen bakkers en vissers want onze Jan wordt dan dubbel geteld.
Later wordt aan of ook een rekenkundige kant toegedicht. Die lijkt ook verdacht veel op optellen `Jan is bakker of visser’ verwijst (weer) naar de vereniging van de verzamelingen bakkers en vissers. “Jan behoort tot de verzameling die het resultaat is van de samenvoeging van de bakkers en de vissers. Daar moet je nog de doorsnede van aftrekken, omdat Jan niet tegelijk bakker en visser zou kunnen zijn”. Dat is nou jammer, want de tweede helft van de zin is nogal ongelukkig.
Als het er om gaat de bakkers en vissers bijeen te nemen dan is weglaten van de doorsnede niet nodig: iemand mag best bakker en visser tegelijk zijn. Als het om het totale aantal mensen gaat moet je, als boven, het anatal mensen in de doorsnede aftrekken van de som van de twee aantallen om dubbeltellen te voorkomen.
De tweede helft is ongelukkig omdat hij niets uitlegt: door het `zou kunnen zijn’ laat hij in het midden of Jan twee beroepen uitoefent, of niet en maakt hij het `omdat’ niet waar.
Ik proefde daar een beetje het verschil tussen het exclusieve of en het inclusieve of maar het kwam niet geheel uit de verf. In de omgangstaal is of veelal exclusief: een koekje of een snoepje, maar niet allebei. In de wiskunde gebruiken we het inclusieve of, een beetje uit gemakzucht maar vooral omdat het in de Logica allemaal een stuk mooier werkt.
Met de tweedeling aan het eind kan ik het wel eens zijn: er zijn twee soorten voegwoorden, die in de ene groep gedragen zich als binaire operaties (denk aan +, ∪ ∩, …) en die in de andere als binaire relaties (≤, =, ≥, ⊆, …). En daar was het in het artikel om te doen: proberen een vinger te krijgen achter het verschijnsel dat je sommige voegwoorden `binnen/buiten de haakjes kunt halen’. De zinnen `Jan is bakker en Jan is visser’ en `Jan is bakker en visser’ betekenen hetzelfde en zijn syntactisch correct. Maar van `Ik ga naar buiten omdat ik wil hardlopen’ kun je niet `Ik ga naar buiten omdat wil hardlopen’ maken; `omdat’ is hier een binaire relatie en die kun je ook in de wiskunde niet buiten de haakjes halen: 5+a=5+b is niet hetzelfde als 5=a+b.
Ten slotte
Om het werken met voegwoorden met rekenen te vergelijken ligt voor de hand maar is niet de juiste keuze. Beter is het naar de Boolese Algebra te kijken (spreek uit: Boelse Algebra). Deze is voortgekomen uit het werk An Investigation into the Laws of Thought van de Ierse wiskundige George Boole. Daarin wordt gerekend met ∧ (en) en ∨ (of), volgens regels die een beetje op die van het gewone rekenen lijken maar ook niet meer dan een beetje.
Veel van wat in het artikel wordt besproken kan hiermee geanalyseerd worden. De ervaring leert dat de studenten met dat rekenen niet zoveel moeite hebben. Het kost ze (en niet alleen de studenten) veel meer moeite normale zinnen correct naar dit formalisme te vertalen.

Recent Comments