Posted in 2018
Het Probleem uit Katowice
De klimaatttop in Katowice verliep/verloopt moeizaam. Maar het klimaat is niet het enige probleem dat aan Katowice verbonden is.
Het probleem uit Katowice gaat over iets totaal anders. Eén manier om het in te leiden is als volgt. Een eenvoudige opgave: stel dat twee verzamelingen evenveel punten hebben, bewijs dat ze evenveel deelverzamelingen hebben.
Dat klinkt voor de hand liggend en het bewijs is, zeker voor een eerstejaarsstudent, niet moeilijk. De juiste wiskundige formulering van `X en Y hebben evenveel elementen’ is er bestaat een bijectie (ook wel een-een-correspondentie genoemd) f:X→Y tusen de twee verzamelingen. Uit die bijectie maak je met gemak een bijectie F tussen de families deelverzamelingen: F(A)=f[A].
Het omgekeerde probleem zou zijn: stel dat twee verzamelingen evenveel deelverzamelingen hebben, bewijs dat ze evenveel punten hebben.
Dat is een stuk lastiger op te lossen; het lukt nog wel voor eindige verzamelingen want een verzameling met n punten heeft 2n deelverzamelingen en als 2m=2n dan volgt m=n. Echter, dat gebruikt extra informatie, meer dan alleen het bestaan van de bijectie F tussen de families deelverzamelingen. En, geloof het of niet: met alleen de informatie dat zo’n F bestaat is de opgave niet te maken. Dat volgt uit het werk dat Paul Cohen heeft gedaan bij zijn deel van de oplossing van Cantor’s Continuumhypothese: daarbij creërde hij een situatie met twee oneindige verzamelingen met evenveel deelverzamelingen maar niet met evenveel punten.
De som wordt maakbaar als we aannemen dat de bijectie wat meer structuur heeft; als je bijvoorbeeld eist dat F en zijn inverse de deelverzamelingrelatie bewaren, dat wil zeggen A⊂B dan en slechts dan als F(A)⊂F(B), dan kun je wel een bijectie tussen de verzamelingen X en Y maken: F moet namelijk de éeacute;npuntsverzamelingen op elkaar afbeelden en dat geeft automatisch de gewenste bijectie.
In de wiskunde is het soms zo dat we `kleine’ verzamelingen verwaarlozen; zo kunnen we afspreken dat we verzamelingen die maar een eindig aantal punten verschillen als gelijk beschouwen. Dat nu leidt ons tot Het Probleem van Katowice: als je weet dat er afbeelding is die bijectief is en ⊂ respecteert, waarbij eindige verschillen er niet toe doen, kun je dan een bijectie tussen de gegeven verzamelingen maken?
Dat probleem is een stuk moeilijker dan de andere maar het is opgelost, bijna: het antwoord is bijna altijd ja, er zijn twee oneindige verzamelingen, met verschillende aantallen elementen, waarvoor we nog niet hebben kunnen bewijzen dat zo’n bijna-bijectie niet bestaat.
Voor wie meer wil weten: hier is een overzicht van het probleem. Met een waarschuwing: zonder een behoorlijke dosis wiskundige basiskennis is het artikel lastig te lezen.
En waarom is dit Het probleem uit Katowice? Het werd opgeworpen door een student aan de Silezische Universiteit in Katowice en omdat het overgebleven geval zo weerbarstig is gebleken heeft het probleem onder wiskundigen deze naam gekregen.
Een vierkante seconde
Een tip voor een niet-standaard uitstapje in Delft: ga een vierkante seconde bekijken.
Delft heeft een mooie binnenstad maar in de buitenwijken kun je ook aardige dingen zien. Neem tram 1 richting Tanthof, stap uit bij de halte Van der Slootsingel, loop de straat met die naam helemaal uit en ga dan rechtsaf het park Buitenhof in. Op een zacht glooiende helling ligt het, een kunstwerk met de naam Een Vierkante Seconde. Je moet echt de helling op want anders zie je de stenen die het vierkant vormen niet.
Waarom `vierkante seconde’?
Als je nauwkeurig wil aangeven waar je bent dan geef je je coördinaten door met behulp van het systeem dat daar al een paar eeuwen voor gebruikt wordt: lengte- en breedtegraden. Op de aarde zijn (denkbeeldig) twee stelsels lijnen getrokken: van de noord- naar de zuidpool (meridianen), en loodrecht daarop, evenwijdig aan de evenaar dus (parallellen).
De meridiaan die door the Royal Observatory in Greenwich loopt heet de nulmeridiaan; samen met de evenaar vormt hij een soort assenkruis, met de evenaar als x-as en de nulmeridiaan als y-as.
Het snijpunt van de nulmeridiaan en de evenaar is de oorsprong. In plaats van x- en y-coördinaten spreken we van, respectievelijk, lengte en breedte en in plaats van positief of negatief zeggen we ooster- en westerlengte, en noorder- en zuiderbreedte.
De eenheid die gekozen is om lengte en breedte uit te drukken is de graad; dat is natuurlijk omdat alle lijnen (delen van) cirkels zijn. Dat is ook handig omdat de parallellen niet allemaal evan lang zijn: de `parallel’, bijvoorbeeld, aan de noordpool bestaat uit maar één punt.
Beide assen zijn in graden verdeeld. De evenaar in twee keer 180 graden: west en oost, als je de nulmeridiaan doortrekt krijgt je de meridiaan op 180° west en oost. De nulmeridiaan is in twee keer 90° verdeeld, noord en zuid.
Nu is nulmeridiaan van de evenaar tot de noordpool 10.000 km lang (per definitie) en dus is één graad ongeveer 111 km lang. Dat is nog vrij veel en daarom zijn de graden weer in 60 mminuten verdeeld, die 60 is een overblijfsel van de 60-tallige schrijfwijze voor getallen uit het oude Babylon. Een minuut langs de nulmeridiaan is ongeveer 1850 m lang; en dat is nu net de definitie van een zeemijl.
De minuten zijn zelf weer in 60 seconden verdeeld en een seconde langs de nulmeridiaan is dus zo’n 30 m lang.
Langs de parallellen worden de graden, minuten en seconden steeds korter. Als je in Park Buitenhof aankomt en het kunstwerk bekijkt zul je zien dat het er niet als een vierkant van 30 bij 30 meter uitziet. Je kunt aan het kunstwerk Geografische Plaatsbepaling Delft (dat is de officiële naam) zien hoeveel korter een seconde op onze breedte geworden is. Het kunstwerk is namelijk een vierhoek die door twee parallellen en door twee meridianen begrensd is.
Op de foto’s van de vier hoeken kun je zien welke lijnen dat zijn:
- de meridianen op
- 04° 20′ 07” O. L. en
- 04° 20′ 08” O. L.,
- en de parallelen op
- 51° 59′ 29” N. B. en
- 51° 59′ 30” N. B.
Ik ben de hele vierhoek rondgelopen; in de noord-zuidrichting had ik dertig stappen nodig en in de oost-westrichting maar negentien.
 |
 |
 |
 |
Voor de wiskundigen: Welke functie bepaalt de lengte van een seconde langs een parallel? Kloppen mijn gemeten lengten ongeveer?
Andere zaken
In het blad Pythagoras is ook al eens een stukje over de vierkante seconde verschenen. Naar aanleiding hiervan ontdekte ik dat je op moet passen als je met een GPS-apparaat in de hand op zoek gaat naar het kunstwerk. Toen de vierhoek werd gelegd (1970) gebruikte men in Nederland het systeem ED50, sindsdien is het systeem WSG 84 in gebruik genomen. Het verschil tussen die systemen is ongeveer 100 meter; met een apparaat dat op WSG 84 is ingesteld loop je het risico in een van de sloten rond het park terecht te komen. In dit document kun je meer lezen over het omrekenen tussen de twee systemen.
In een video van Ionica Smeets over de vierkante seconde wordt hier voor gewaarschuwd. Naar aanleiding van die video is er een Geocache bij het kunstwerk gemaakt.
Op de Kunstwachtwebsite kun je ook over Geografische Plaatsbepaling lezen. En op de website van een van de makers, Nelis Oosterwijk, kun je wat ontwerpschetsen zien.
En tau rund jorden, II
Dette er andre delen av en oversettelse av en artikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger). Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen? Kan vi uttrykke høyden i lengden vi spleiset inn?
I går vi så at når vi tar en tau som er en meter langre enn jordens omtrekk og drar tauen strammt ved Nordpolen så skal det høyeste punktet være på 121 meter og lit mer. I dag skal vi lage en enkel formel med radiusen og ekstra lengden i som gir en god approksimasjon av høyden.
En effektiv approksimasjon
Her er tegningen fra i går igjen
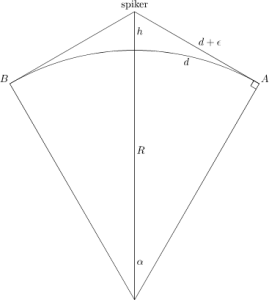
Fra Pythagoras sin læresetning lærte vi at
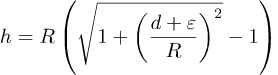
Fra bildet ser vi også at
![]()
Dette kan kombineres til denne ligningen
![]()
Nå har vi et uttrykk for h som bruker R og α men vi trenger et som bruker ε. Dette må gjøres implisitt fordi α er en løsning av
![]()
og der er ingen `pen’ (eller stygg) formel for løsningene.
Som vi så i går er vinkelen α veldi liten (0.006176 radianer). Nå er det slik at α+α3/3 er en veldi bra approksimasjon av tanα. Hvis vi setter dette uttrykket i ligningen så får vi
![]()
Også tanα er veldi liten.
Og for x nær 0 har vi √(1+x)≈1+½x; nå kan vi forenkle formelen for h til en approksimasjon
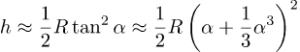
Neste steg er å skrive ut kvadraten
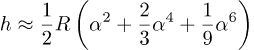
Når vi setter i tallene så får vi Rα2=242.8 m, Rα4=0.009 m og Rα6=3.5×10-7 m. Vi derfor kan trygt kaste fjerde og sjette potensene og så får vi denne approksimasjonen for h:
![]()
Lit lengre siden fant vi at
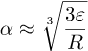
Vi setter det inn i approksimasjonen og får
![]()
Nå bruker vi verdien av R og får til slutt
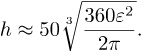
Det flotte med denne formelen er at den gir nesten samme svaret som i går: setter vi inn ε=0.5 så får vi h≈121.4 m igjen.
Oppgav
Sett inn ε=0.005 in formelen vår. Hvor mye forskjeller resultatet fra verdien av h som vi fikk i går?
Exercise
Undersøk hvor bra approksimasjonen √(1+x)≈1+½x er. For eksempel, sammenlign (1+½x)2 med 1+x; for hvilken x er forskjellen liten nok til å bli kastet? Er du enig i hvordan approksimasjonen brukes her?
Bemerkning
Vi kan isolere ε i formelen:
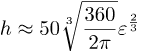
dette gir viktig kvalitativ informasjon: h er omtrent lik en konstant ganger ε2/3.
Hvis du er kjent med Taylorpolynomer kann det være gøy å finne ut hvor stor feilen er (hvilken potens av ε) i denne approksimasjonen.
En tau rund jorden, I
Dette er første delen av en oversettelse av en art ikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger).
Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen?
Fast alle har hørt om følgende oppgaven. Vi tar en tau og strekker den rund jorden, langs polene, slik at den sitter tett. På Nordpolen spleiser vi inn en ekstra meter tau. Så drar vi, og mange folk rund jorden, tauen opp slik at den er overalt like høyt over jordoverflaten; den blir en sirkel igjen. Hvor høyt kommer den til å bli? Kan en mus komme seg under tauen?
Svaret, tauen skal være overalt 16 centimeter høyt, blir en overraskelse for mange folk. inntil du utfører beregningen. Vi begynner med en tau som er 2πR lang, der R er jordens radius. Oppgaven er å bestemme radiusen til sirkelen som er en meter lengre. Det vil si: bestem R’ slik at 2πR’=2πR+1. Men det er lett å gjøre: divider med 2π, så får vi R’=R+1/(2π)≈R+0.159.
Beregninger viser at verdien av R er ikke viktig: hvis du forlenger en sirkel med en meter så forlenger du radiusen med nesten 16 centimeter.
Vi henger jorden på en spiker
Men hva om vi drar opp tauen bare på Nordpolen til den er helt stramm igjen? Som om vi skule bruke tauen til å henge jorden på en spiker. Hvor høyt kommer spikeren til å bli over Nordpolen? Kan en isbjørn komme seg under tauen?
Her er en tegning som viser hva vi prøver å gjøre.

Det er lit enklere med bokstaver: R er jordens radius, ε er halvparten av tauen vi spleiset inn (en halv meter altså) og h er svaret på spørsmålet.
Buen d viser distansen fra Nordpolen til begge punktene der tauen sist berører jorden.
Vi har en rett vinkel i A (og B) fordi linjen fra A til spikeren er en
tangent til sirkelen. Nå kan vi finne en formel for h.
Vi begynner med Pythagoras sin læresetning:
![]()
og så h+R=±√(R2+(d+ε)2), eller
![]()
Dersom h er positiv må vi ta plussen, og
![]()
Vi tar R utenfor parentesen og får
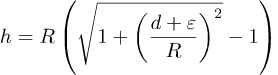
Det vi ikke vet her er verdien til d. Vi bruker radianer, og derfor d=αR eller α=d/R fordi, som vi skal se, det er enklere å lage en ligning for α.
Fra bildet ser vi hva tangensen til vinkelen α er:
![]()
og derfor
![]()
eller
![]()
Så, vår α er en løsning på siste ligningen.
Nå trenger vi noen tall. Jordens omkrets er, per definisjon, 40.000 km
(se illustrasjonen her). Derfor R=40.000.000/(2π) m og, selffølgelig, ε=½ m. Det betyr at vi må løse
![]()
Det finnes ingen enkelt formel for løsningen; det beste vi gjøre er å løse ligningen numerisk. De fleste grafiske kalkulatorene kan gjøre det for deg og jeg fikk denne løsningen: alpha;≈0.006176=6.176×10-3 og det betyr at d≈247.040 km. Det er interessant å vite hvor langt fra Nordpolen tauen forlater jorden men vi trenger ikke d i beregningene våre: vi setter α for d/R in formelen for h:
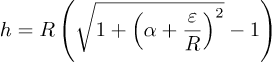
Når vi taster alle tallene in kalkulatoren får vi h≈121.4 m.
Oppgave
Gjør alt igjen men nå spleiser du inn bare en centimeter tau. Hvis tauen er lett nok kan du dra den stramm uten hjelp?
Selv om vi ikke har en eksakt formel for h som involverer ε og R kan vi noe om relasjonen mellom de tre størrelsene. Jeg skal skrive noe om det senere, in andere delen av denne historien.
Hon hade blivit kissnödig
Sometimes I read a book for an odd reason. In this blog a reader expressed surprise that `pee’ was being used as a noun to indicate the act of peeing, as in “She needed a pee”. This piqued my interest not because of the issue of noun versus verb but because I wanted to know what was in the Swedish original, `Solstorm’ by Åsa Larsson.
The original sentence was “Hon hade blivit kissnödig”. I found it difficult to come up with a faithful translation that is as compact as the original. Both “She needed to pee” and “She needed a pee” come close but they do not convey the exact meaning. A too-literal translation runs as follows: “She had become piss-necessary”; the `necessary’ chafes here. The term `piss-pressed’ might be better, but I could not come up with one word that describes the state of having the need to micturate.
The Swedish `att kissa’ means `to piss’ and it is an obvious candidate for a false friend between that language and English. It turns out that Google Translate has problems with the sentence too. When I had it translate “Hon hade blivit kissnödig” I got
- English: She had become kissed
- Dutch: Ze was gekust
- Norwegian: Hun ble blitt kysset
Be careful what you ask for in Sweden.
Servetringen en Cavalieri
In haar laatste column voor de vakantie gaf Ionica Smeets de lezers een puzzel van Martin Gardner mee. Dit stukje gaat over een aspect van de puzzel dat in de column een beetje onbelicht blijft maar dat wel de sleutel tot een oplossing `uit-het-hoofd’ is.
Het probleem gaat als volgt: neem een bol en boor daar een cilindrisch gat in en wel zo dat je een servetring overhoudt die 6 cm dik is. Vraag: wat is het volume van die servetring. NB de as van de cilinder gaat door het middelpunt van de bol; de servetring is dus echt een ring.
Je kunt dat volume op een paar manieren bepalen. Leerlingen die wiskunde B hebben gedaan weten hoe ze volumes van wentellichamen met behulp van integralen uit kunnen rekenen. Als je toevallig wat formules voor volumes van bepaalde delen van een bol paraat hebt reken je het ook zo uit. Wat opvalt als je zo’n weg volgt is dat de straal van de bol er kennelijk niet toe doet. Dit is waarom Ionica dit een krankzinnig raadsel noemt: het lijkt of er een gegeven ontbreekt, namelijk de straal van de bol, maar achteraf blijkt dat niet zo te zijn. Dat had je dan op het spoor van een oplossing `uit-het-hoofd’ kunnen zetten: in de vraag wordt de straal niet genoemd, dan doe die er kennelijk niet toe, maar dan kan ik ook een heel makkelijk geval bekijken.
Maar goed, waarom doet die straal er niet toe?
De leerlingen die het volume met behulp van integralen gaan uitrekenen zien het meteen: in de integraal die uitgerekend moet worden is de straal van de bol verdwenen (hij komt twee keer in het kwadraat voor, maar die kwadraten worden van elkaar afgetrokken).
En wat doet iemand die niet kan integreren? Die gebruikt iets dat teruggaat tot Archimedes maar dat tegenwoordig bekend staat als het principe van Cavalieri.
Leg zo’n servetring op de grond en doe alsof het middelpunt van de bol op hoogte 0 ligt (zie het plaatje in de column). Snij nu de servetring met een wiskundige kaasschaaf in flinterdunne plakken. Bekijk de ringvormige plak op hoogte z. Die ring heeft een buitenstraal en een binnenstraal. De buitenstraal is gelijk aan √(R2-z2) en de binnenstraal is gelijk aan de straal van de cilinder en die is gelijk aan √(R2-32). De oppervlakte van de ring is dan gelijk aan π(R2-z2-R2+32) ofwel π(32-z2) en dat is onafhankelijk van de straal van de bol.
Het principe van Cavalieri zegt, toegespitst op dit geval: als je twee lichamen hebt van gelijke hoogte en op elke hoogte zijn de oppervlakten van de horizontale plakken uit de lichamen even groot dan zijn de volumes van de lichamen aan elkaar gelijk.
En daarom kun je volstaan met het probleem in een heel speciaal geval op te lossen.
Bijna twintig jaar geleden stond in Pythagoras een stukje over de manier waarop Cavalieri zijn principe gebruikte om oppervlakten te bepalen.
Het klinkt wel mooi dat principe van Cavalieri maar klopt het eigenlijk wel? Hoe zou je het bewijzen? Dan komen we vanzelf uit op de vraag wat `volume’ eigenlijk betekent. Na veel nadenken is daar een werkbare definitie van gegeven en gaat het bewijs van het principe via de integraal die de wiskunde-B-ers voor de oplossing van Gardner’s probleem zouden kunnen gebruiken.
Mathsplaining
Gisteren gebruikte Aafke Romeijn in een tweet de frase mansplaining tot de macht oneindig. Ik kon nog net virtueel op mijn tong bijten maar nu moet ik toch even aan het mathsplainen.
Dat “tot de macht oneindig” klinkt wel indrukwekkend maar de kans is groot dat je er niet mee bereikt wat je wilt. Want wat betekent “tot de macht oneindig” eigenlijk? Wiskundig dan. En wat betekent “oneindig”? In dit geval zullen we het maar op het ∞ van de Analyse houden. Dan betekent “mainsplaining tot de macht oneindig” niets anders dan “de limiet van mainsplainingn voor n naar ∞”.
OK, maar dan moeten we dus eerst betekenis hechten aan “mansplaining-kwadraat”,
“mansplaining tot de derde macht”, … en vervolgens het gedrag van die machten van mansplaining bestuderen. Tsja, en dan komt het: hoe vermenigvuldig je mansplaining met zichzelf? Wiskundig betekent het woord niets maar we kunnen wat vermenigvuldigbare zaken langslopen.
We kunnen getallen vermenigvuldigen, en dus ook machtsverheffen. Maar dan komt het: is mansplaining negatief? Voor velen wel, denk ik. Jammer dan, maar dan is het kwadraat positief, de derde macht negatief, de vierde macht positief, … dan kun je het schudden: de limiet bestaat niet. Tenzij, …, je vindt dat mansplaining eigenlijk wel zielig is en weinig waarde heeft, zeg absolute waarde kleiner dan 1. Dan convergeren die machten naar 0 en dan is mansplaining tot de macht oneindig dus gelijk aan 0. Ik weet niet of dat Aafke Romeijn voor ogen stond.
Mansplaining is natuurlijk irreëel en irrationaal; dat lijkt wiskundig niet goed te gaan maar je kunt het interpreteren als “een complex getal met irrationaal argument”. Wiskundigen zien hier meteen een woordspeling: het woord `argument’ heeft in de wereld van de complexe getallen zijn geheel eigen betekenis. Dan leidt machtsverheffen tot een duizeligmakend ronddraaien; het hangt van de absolute waarde af of dit naar 0 convergeert, of naar ∞, of zonder limiet de eenheidscirkel blijft rondlopen. (Om andere mathsplainers de wind uit de zeilen te nemen: dat argument is een irrationaal veelvoud van π.)
Een mansplainer projecteert zijn eigen meningen en gedachten op hetgeen hij aan het mansplainen is. Dat leidt tot een wat merkwaardige situatie: wiskundig is het kwadraat van een projectie de projectie zelf. En dus is elke macht van mansplaining gelijk aan mansplaining zelf, met als conclusie dat mansplaining tot de macht oneindig gewoon mansplaining is. Eigenlijk wel een mooie conclusie: mansplaining is al zo erge flauwekul dat het zijn eigen oneindige macht is.
Wiskunde B (vwo): eerste en tweede zitting
Er was de laatste dagen nogal wat ophef over het verschil in niveau tussen de eerste en tweede zitting van het eindexamen Wiskunde B (vwo). Tijd voor een vergelijking.
Ik heb die beide examens gemaakt en mijn uitwerkingen, met commentaar, via dit blog bekend gemaakt: kijk hier voor de eerste en hier voor de tweede zitting. Ik kreeg de vraag of mij het niveauverschil tussen de beide examens niet was opgevallen.
De eerlijkheid gebiedt mij te bekennen dat ik de vragen van de eerste zitting al weer vergeten was toen die van de tweede zitting bekeek. Ik heb de beide examens, en mijn uitwerkingen, nog eens naast elkaar gelegd om te zien wat de verschillen waren.
Bij oppervlakkige lezing zijn de examens nogal verschillend: de `contextvragen’ hebben geheel verschillende onderwerpen en de manieren waarop zaken als differentiëren, integreren en analytisch meetkundige zaken worden aangesneden zien er anders uit.
Maar dat is aan de oppervlakte; als je wat dieper/verder kijkt zie je dat de onderliggende wiskunde ongeveer gelijk is. Herstel: ik zie dat er weinig verschil is. Ik heb lijstjes gemaakt met wat gedaan moest worden en hoe moeilijk het was om het te doen. En ik kon niet echt een groot verschil zien.
De vraag is dan waarom de tweede zitting zoveel moeilijker gevonden werd dan de eerste. Voor mij werd dat duidelijk na een reactie op mijn blogpost over de tweede zitting: Valerie wijst er terecht op dat ik een beroepswiskundige met veel ervaring ben en ze legt de vinger op een zere plek die ik niet eens opmerkte: de uitgebreide inleidingen die voor mij de sommen nogal flauw lieten worden zorgden kennelijk bij veel leerlingen voor verwarring.
Als je op deze manier naar de examens kijkt kun je wel degelijk grote verschillen aanwijzen. Neem bijvoorbeeld de openingsvragen. Bij de eerste zitting: zonder veel omhaal van woorden word opgeschreven wat gedaan moet worden. Bij de tweede zitting: vooral bij vraag 2 een lange inleiding die waarschijnlijk voor velen versluierde dat je alleen maar de gegeven functie h in 0 hoefde te differentiëren.
Bij de eerste zitting waren vragen 3, 4, en 5 ook lekker kort en krachtig; bij de tweede zitting waren deze ingebed in grote stukken tekst over smeltende bolletjes ijs. Ik kan me voorstellen dat alleen al door deze verschillen aan het begin de tweede zitting als zwaarder werd ervaren dan de eerste.
Eindexamen Wiskunde B (2018-06-20)
Gisteren was de tweede zitting van het eindexamen Wiskunde B van het vwo (correctievoorschrift). Hier is mijn uitwerking, met commentaar (en de gebruikte Maplecommando’s).
Ik vond het examen, net als dat van het eerste tijdvak niet echt uitdagend; er was weer één situatie-met-context, dit keer een smeltend ijsbolletje. Ook deze keer werden de sommen uitgebreid ingeleid en was de eigenlijke opgave telkens teleurstellend eenvoudig.
Het Compactheidsbeginsel
Twee recente artikelen op Kennislink hebben iets gemeen. Dat gemeenschappelijke is een belangrijk stuk gereedschap uit de Wiskunde dat bekend staat als het Compactheidsbeginsel.
In 2016 werd een kleuringsprobleem voor de natuurlijke getallen opgelost: is het mogelijk de natuurlijke getallen in tweeën te delen op zo’n manier dat beide delen geen enkel Pythagoreïsch drietal bevatten? Het antwoord is: “nee”. Zoals op Kennislink te lezen is is er iets meer ontdekt: bij elke verdeling van {1,2,3,…7825} in twee delen moet een van de delen een Pythagoreïsch drietal bevatten en er is een verdeling van {1,2,3,…,7824} waarbij geen van de beide delen een bevat.
Voor de goede orde: een Pythagoreïsch drietal is een drietal natuurlijke getallen (a,b,c) dat voldoet aan a2+b2=c2. Ook wordt het probleem vaak in termen van kleuringen geformuleerd: de verdeling wordt weergegeven door elk natuurlijk getal rood of blauw te kleuren.
Begin van deze maand werd vooruitgang geboekt bij een kleuringsprobleem in het platte vlak: in hoeveel verzamelingen moet je de punten in het vlak minimaal verdelen opdat geen enkel deel twee punten bevat die afstand 1 hebben. Er was lang bekend dat dat minimale aantal ten minste 4 en ten hoogste 7 is; nu is bekend dat het ten minste 5 moet zijn. Okk hier is al aan een eindige verzameling punten te zien dat bij elke verdeling in vier stukken er altijd een stuk is dat twee punten met afstand 1 bevat.
Waarom is dat? Het zou toch bij het eerste probleem zo kunnen zijn dat bij verschillende kleuringen de drietallen één kleur krijgen steeds hoger in de natuurlijke getallen moeten zitten. Maar kennelijk is het zo dat, ongeacht de kleuring er al een éénkleurig drietal is in {1,2,3,…,7825}.
Het geheim is een stelling van De Bruijn en Erdös; deze zegt dat bij elk kleurings probleem het volgende geldt: als elke eindige verzameling een `goede’ kleuring heeft dan is er een `goede’ kleuring voor de hele verzameling. Dat kun je ook als volgt contrapositief formuleren: als elke kleuring van de hele verzameling `slecht’ is dan is er een vaste eindige verzameling waarvoor elke kleuring `slecht’ is. In April 2014 is over deze stelling een artikel in Pythagoras verschenen.
Het voordeel van dit Compactheidsbeginsel is dat men voor positieve resultaten alleen naar eindige verzamelingen hoeft te kijken; dat kan de bewijzen aanzienlijk vereenvoudigen. Het nadeel is dat het niet constructief is: het geeft geen enkele informatie over de grootte van de vaste eindige verzameling waarvoor elke kleuring `slecht’ is. Dat laatste is te zien aan de resultaten waarover op Kennislink bericht werd; de zoektochten naar de eindige verzamelingen en de verificaties dat ze werkten kostten veel tijd en moeite.

Recent Comments