Posted in 2017
Snel ordenen
Nog een vraag van de wisfaq:
Ik ben me aan het voorbereiden voor toelatingsexamen aan de Koninklijke Militaire School en kwam volgende vraag tegen:
Sorteer a, b en c volgens stijgende waarden: a=√23; b=1199/250; c=959/200
Nu vroeg ik me af hoe ik dit efficiënt kan doen en zonder rekenmachine weliswaar!
Hoe doe je zoiets snel? Als ik veel haast heb bereken ik misschien 1199×200 en 959×250. Er geldt namelijk dat b>c precies als 1199×200>959×250 (via kruislings vermenigvuldigen) en daarnaast zou ik snel de kwadraten van b en c bepalen en met 23 vergelijken.
Die vermenigvuldigingen kosten wel wat tijd want de getallen zijn een beetje groot. Daarom kan het handig zijn iets beter naar de getallen te kijken. Dan blijkt dat die twee breuken hetzelfde gehele deel hebben, namelijk 4, en dat wat overblijft snel te vergelijken is:
1199/250=4+199/250=4+796/1000 en 959=4+159/200=4+795/1000 en nu zijn b en c in ieder geval heel eenvoudig te vergelijken: b>c.
En hoe zit het met √23? Het kwadrateren van b en c kan iets sneller als je het indirect doet: schijf b=5-204/1000 en c=5-205/1000, en gebruik de bekende formule (x-y)2=x2-2xy+y2. Dan blijkt dat
- b2=23-4/100+(204/1000)2, en
- c2=23-5/100+(205/1000)2.
Nu is (204/1000)2 net iets meer dan (2/10)2=4/100, dus b2 is net iets groter dan 23.
Ook (205/1000)2 is iets meer dan 4/100 maar niet te veel: het is kleiner dan het makkelijkere kwadraat (21/100)2=4,41/100 en dat is weer kleiner dan 5/100, dus c2 is kleiner dan 23.
Conclusie: 959/200<√23<1199/250.
Ik vind dit een aardige opgave omdat met weinig niet al te moeilijke vermenigvuldigingen en delingen drie getallen die heel dicht bij elkaar liggen toch mooi onderscheiden kunnen worden.
Tien getallen rond een tafel
Op de Wisfaq stond laatst weer een aardige vraag:
Natuurlijke getallen van 1 tot en met 10 zijn geordend in een willekeurige volgorde rond een cirkel. Je kan steeds (dus in een cirkel is er minstens 1 geval) 3 opeenvolgende getallen vinden waarvoor de som groter is dan 17.
Hoe zou je zoiets aanpakken? Meestal kun je wel iets over die sommen zeggen waardoor blijkt dat er één (of meer) over een bepaalde grens moet gaan, bijvoorbeeld als de som van al die sommen groot moet zijn.
In dit geval kunnen de tien sommen bij elkaar optellen; dan tellen we elk getal 1, 2, …, 9, 10 driemaal mee dus we krijgen als totaal 3×(1+2+…+9+10)=3×55=165.
Dat betekent dat niet alle sommen kleiner dan 17 kunnen zijn, want dan zou hun totaal niet groter zijn dan 10×16=160. Het eerste succes is binnen: we zien vrij goedkoop dat tenminste één drietal een som van 17 of meer moet hebben.
Vervolgens heb ik een paar vellen kladpapier gebruikt om de getallen zo rond de tafel te plaatsen dat alle sommen niet groter waren dan 17. Waarom? Voor mij is het zo dat als ik zoiets vaak genoeg mis zie lopen ik een idee krijg hoe te bewijzen dat het gevraagde waar is: de reden van het mislopen is soms een sleutel tot een bewijs.
In dit geval bleek het lastig het gemiddelde van de sommen in de buurt van 16,5 te houden, dus ging ik kijken hoe dat gemiddelde gelijk kon zijn aan 16,5 terwijl alle sommen niet groter dan 17 mochten zijn.
Na wat proberen bleek dat ten minste vijf van de sommen gelijk aan 17 moeten zijn; immers, bij vier (of minder) sommen gelijk aan 17 zijn de andere zes (of meer) sommen niet groter dan 16 en dus zou het totaal niet groter zijn dan 4×17+6×16=164, en dat is net te klein.
Daarnaast bleek dat er ook maar ten hoogste vijf sommen gelijk aan 17 konden zijn. Dat was zo duidelijk dat ik het eerst over het hoofd zag: neem vier getallen op een rij: x1, x2, x3, x4.
Omdat x1≠x4 volgt dat x1+x2+x3≠x2+x3+x4. Van elk tweetal naast elkaar liggende sommen is er dus hooguit één gelijk aan 17.
Als we de tafel rondlopen zien we dus nooit twee sommen gelijk aan 17 naast elkaar; dat betekent dat we niet meer dan vijf maal een 17 zullen zien.
Nu weten we dat er precies vijf sommen gelijk zijn aan 17, maar dan moeten de andere vijf sommen gelijk zijn aan 16 (om het totaal op 165 te houden) en de sommen 17 en 16 komen dus om en om voor.
Loop nu de tafel rond en noem de getallen die je ziet x1, x2, … en begin op een plek waar x1+x2+x3=17. Dan moet vervolgens gelden
- x2+x3+x4=16, en
- x3+x4+x5=17, en
- x4+x5+x6=16, en
- x5+x6+x7=17.
Trek de tweede vergelijking van de eerste af, je ziet x1-x4=1.
Trek de vierde vergelijking van de vijfde af, je ziet x7-x4=1.
Maar nu volgt x1=x7 en dat kan niet want we hadden tien verschillende getallen rond de tafel gezet.
Conclusie: elke poging alle tien de sommen kleiner dan of gelijk aan 17 te houden zal falen. Hoe je de getallen ook neerzet, er is een som die groter is dan 17.
In de Wiskunde heet zoiets een (niet-constructief) existentiebewijs: we laten zien dat iets moet voorkomen maar er is geen recept dat het gewenste verschijnsel aanwijst. Het bewijs geeft (slechts) aan hoe een poging zal stranden: je moet vijf keer 17 als som hebben, en vijf keer 16, en die moeten om en om voorkomen en dan loopt het echt mis: twee verschillende getallen moeten gelijk zijn.
Opdracht.
Om te puzzelen: is er een verdeling met alle sommen niet groter dan 18? Ik heb het nog niet geprobeerd.
Twee machten vergelijken
Op een paar plekken op het web dook de vraag weer eens op wie groter is: 10001001 of 10011000.
Je kunt die vraag op meer dan één manier/niveau beantwoorden. Achtereenvolgens bekijken we
- Rekenmachientje: neem links en rechts de duizendstemachtswortel en vergelijk 10001,001 met 1001. Dank aan Frank Boers (via `Leraar Wiskunde’ op Facebook).
- Logaritmen en rekenmachientje: de logaritmen (basis 10) kunnen eenvoudig vergeleken worden en we krijgen informatie over het aantal cijfers in beide machten.
- Natuurlijke logaritmen en integralen: de natuurlijke logaritmen van de machten kunnen, met een beroep op een eenvoudige eigenschap van de integraal `met de hand’ vergeleken worden.
- Binomium van Newton: schrijf (1000+1)1000 uit met behulp van het binomium en laat zien dat de termen in de som steeds groter worden; hiermee is de macht snel af te schatten.
- Binomium van Newton (bis): het quotient van (1000+1)1000 en 10001001 is met behulp van het binomium af te schatten met 3/1000.
- Het getal e: met behulp van een definierende rij voor e kan de vorige afschatting verbeterd worden tot e/1000.
- Functieonderzoek: in het algemeen geldt: als e<x<y dan yx<xy. Dit volgt door de functie x/ln(x) te bekijken. Dank aan René Pannekoek.
- Gebruik de e-macht: via ex>1+x vind je 10001,001>1000+ln(1000).
De oplossingen vereisen nogal wat wiskundige notatie; daarom heb ik ze hier in een PDF-file neergezet.
Sorteren
In haar column van 1 juli beschreef Ionica Smeets hoe de logistiek van een menselijke keten van de Belgische kerncentrale Tihange naar de Duitse stad Aken haar aan van alles deed denken, behalve kernenergie.
Een van de problemen die bij haar opkwam was het op alfabet sorteren van de schakels in de mensenketen en hoe lang dat zou duren. De sorteermethode waar ze aan dacht bestaat uit het telkens vergelijken van de namen van twee naast elkaar staande personen en die, indien nodig, omwisselen.
Nu kun je zoiets op veel manieren uitvoeren en zo ongeveer het eerste sorteerprogramma dat ik zelf geschreven heb loopt telkens van begin tot eind door de lijst en wisselt verkeerd geordende buren om. Hier is een versie in de taal python (de n is de lengte van de lijst; in python wordt een lijst van lengte n genummerd van 0 tot en met n-1):
for k in range(1,n-1):
for l in range(1,n-k):
if x[l] < x[l-1]:
xx = x[l]
x[l] = x[l-1]
x[l-1] = xx
Het programma is iets versneld: als k=1 staat aan het eind van de binnenste loop het grootste element in x[n-1]; als k=2 staat aan het eind van de binnenste loop het op één na grootste element in x[n-2], enzovoort. Dit betekent dat er slechts n-1 binnenloops uitgevoerd hoeven worden die ook steeds korter worden: l loopt telkens maar tot n-k.
Hoe lang duurt het voor het programma klaar is? Neem aan dat we het alfabetisch van Aken naar Tihange willen sorteren. In het ergste geval, als de lijst al alfabetisch gesorteerd is maar net andersom, van Tihange naar Aken dus, moeten er 50000×49999/2 verwisselingen gedaan worden. Dat zijn er, afgerond, 1,25×109, (veel) meer dan een miljard dus.
Aangenomen dat een verwisseling een seconde kost dan zijn we met mijn programmaatje wat meer dan 39 jaar bezig.
Efficiënter?
Het bovenstaande programmaatje implementeert het zogeheten bubble-sort (de grotere elementen `borrelen’ omhoog door de lijst). Bedenk dat dit bij onze mensenketen neerkomt op het volgende: de hoofdorganisator holt iedere keer keer weer langs de keten mensen en laat telkens verkeerd geordende tweetallen omwisselen. Hierbij staat iedereen vrijwel de hele tijd te niksen.
We kunnen die mensen beter zelf wat laten doen door ze als parallelle processoren te gebruiken. Op elk moment laten we de mensen die dan op een evengenummerde plaats staan zich met een buur vergelijken en, zo nodig, van plaats verwisselen. Op de oneven momenten kijken die mensen richting Tihange en op de even momenten richting Aken.
Dus bij stap 1 laten we alle paren (0,1), (2,3), (4,5), … (49998,49999) vergelijken en, indien nodig, wisselen. Bij stap 2 laten we dat de paren (1,2), (3,4), (5,6), … (49997,49998) doen. Dit gebeurt om en om tot de rij gesorteerd is. Dit proces staat, om een voor de hand liggende reden, bekend als odd-even sort.
Omdat we nu telkens 25.000 verwisselingen tegelijk laten doen kost dit `maar’ 50.000 iteraties. En als iedereen goed meewerkt zijn we dus in 50.000 seconden klaar, dat is wat minder dan 14 uur.
KP checkt: Ruim de helft meer …
Op twitter werd er al schande van gesproken: vandaag (2017-06-27) in NRC: … iets meer dan 100 Euro, ruim de helft meer dan de 46,45 Euro … (NRC Checkt).
Is 100 echt ruim de helft meer dan 46,45? Nee, natuurlijk niet. `Meer’ en `minder’ doe je altijd ten opzichte van het beginbedrag, en dat is hier 46,45. De helft van dat bedrag is 23,225 en `ruim de helft’ is wat subjectief, maar hoger dan 30 zou ik toch niet gaan. Ruim de helft meer dan 46.45 is dus niet meer dan ongeveer 76 a 77.
Ik beoordeel deze bewering van NRC Checkt als ONWAAR.
Overigens zie je zo waar dat `ruim de helft’ vandaan komt: 100 is inderdaad ruim de helft van 100 zelf (namelijk 53,55) meer dan 46.45. Hoe begrijpelijk ook, het is op zijn zachtst gezegd niet handig: het wordt snel onwerkbaar als je bij iedere transactie moet vragen of het om een deel van het begin- of van het eindbedrag gaat.
Om verwarring te voorkomen rekent men altijd vanuit het beginbedrag. In het stuk van NRC Checkt zou dat nog spectaculairder klinken: … iets meer dan 100 Euro, ruim het dubbele van de 46,45 Euro …

On-line is het al verbeterd, maar papier is geduldig.
Herkansing Wiskunde B, 2017
Gisteren was de herkansing Wiskunde B, zie hier voor de opgaven.
Hier is mijn uitwerking met wat opmerkingen.
Raaklijnen aan de aarde, II
Vandaag los ik een belofte van gisteren in door te laten zien wat de twee vragen van gisteren gemeen hebben, naast het feit dat beide iets met raaklijnen aan het aardoppervlak te maken hebben.
De vraag naar de hoogte van het eindpunt van de rechte weg van John Körmeling leidde tot de formule

Gisteren stond er 3000 op de plaats van de w maar ik heb die w ingevoerd om de structuur van de formule duidelijk te maken. Ter herinnering R is de straal van de aarde.
De vraag over de wandeling van Zandvoort naar Scheveningen leidde tot
![]()
Hierin is α de hoek, in radialen, tussen de positievectoren (vanuit het middelpunt van de aarde) van Zandvoort en Scheveningen. Er geldt dat α=d/R, waar d de gelopen afstand is (gemeten langs het aardoppervlak natuurlijk).
Die formules lijken niet echt op elkaar maar voor een wiskundige met haast en zonder rekenmachine op zak zijn ze eigenlijk gelijk. Het punt is namelijk dat w/R en α erg klein zijn (en (w/R)2 nog kleiner). Voor kleine x gelden de volgende benaderingen.
![]()
en
![]()
Voor wie wat weet over Taylorpolynomen komen deze benaderingen niet als een verrassing. Voor wie die polynomen niet kent: de benadering van √(1+x) krijg je door je te realiseren dat (1+x/2)2=1+x+x2/4. Als x heel klein is is x2 nog veel kleiner en dat maakt de benadering goed genoeg. Voor de benadering van cos(x) zonder gebruik van de stelling van Taylor verwijs ik naar dit artikel in Pythagoras; daar wordt ook bekeken hoe goed die benadering eigenlijk is.
Als we de benaderingen gebruiken krijgen we de volgende benaderingen van de
twee hoogtes. Voor de weg:
![]()
Voor de hoogte aan het eind van de wandeling:
![]()
Voor deze laatste benadering doen we twee stappen: de teller wordt R×α2/2=d2/(2R). Nu moeten we nog met 1/(1-α2/2) vermenigvuldigen, maar voor kleine x geldt
![]()
dus vermenigvuldigen we met 1+α2/2 met als resultaat
![]()
Die laatste term is zo klein dat we hem weg mogen laten.
Als we de benaderingen toepassen krijgen we 0.706858347 voor de weg en 113.4114948 voor de wandeling. De verschillen met de antwoorden dan gisteren zijn in de orde van grootte van tienden van milimeters voor de weg en van milimeters voor de wandeling.
Waarom zou je die benaderingen maken? Een rekenmachientje geeft toch meteen een uitkomst, ook met de ingewikkelde formules? Het antwoord is tweeledig. Ten eerste heb je niet altijd een rekenmachine bij de hand en dat worden die formules wat bewerkelijk. Ten tweede, en dat is de eigenlijke reden: aan de benadering kun je vaak beter afzien hoe de uitkomst van de invoer afhangt. In beide gevallen hebben we gezien dat er een kwadratisch verband is: de grafiek van h als functie van w of d is nagenoeg een parabool.
Een ander voorbeeld van het werken met benaderingen is te vinden in dit artikel uit Pythagoras:
Een touwtje om de aarde.
Tot slot wat opdrachten.
Opgave 1. Bereken d4/(4R3); was het gerechtvaardigd die term weg te laten?
Opgave 2. Ga na dat de benadering ook werkt voor de diepte van de ingegraven weg.
Opgave 3. De benadering zijn, natuurlijk, niet exact. Ga na of ze de echte waarden over- of onderschatten (ook voor de ingegraven weg).
Opgave 4 Onderzoek hoe goed de benadering 1+x van 1/(1-x) is.
Raaklijnen aan de aarde, I
Zo af en toe kom ik een vraag tegen die opgelost kan worden door naar een raaklijn aan het aardoppervlak te kijken.
Op de website van De Ingenieur verscheen in januari een stuk over een project van de kunstenaar
John Körmeling: het aanleggen van een echt rechte weg. De bedoeling is dat de weg recht is in de zin van `een rechte lijn’: het wegoppervlak ligt dus in een raakvlak aan het aardoppervlak.
De weg van Körmeling (eigenlijk een schelpenpad) wordt zes kilometer lang, drie kilometer naar beide kanten vanuit het raakpunt. In het stuk wordt verteld dat de weg aan de uiteinden zo’n 70 centimeter boven het aardoppervlak komt te liggen. Ik kreeg van een lezer van Pythagoras de vraag of dat wel klopt; het leek wat weinig.
Op de wisfaq werd bijna hetzelfde gevraagd maar over iets grotere afstand: als ik van Zandvoort naar Scheveningen zou lopen over een rechte weg als die van Körmeling hoe hoog boven Scheveningen komt ik dan uit?
De vragen zijn bijna maar niet helemaal hetzelfde: bij de weg van Körmeling weten we hoe lang de rechte lijn zelf is, en bij de tweede vraag weten we de afstand langs het aardoppervlak. Dat heeft gevolgen voor de vorm van de oplossingen, zoals we zo dadelijk zullen zien.
Eerst een plaatje voor de rechte weg
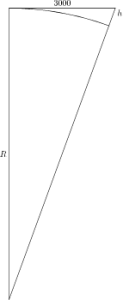
Hier is R de straal van de aarde en h de hoogte van het uiteinde van de weg boven het aardoppervlak. De stelling van Pythagoras brengt hier uitkomst: de onbekende h moet voldoen aan (R+h)2=R2+30002. Als we dit naar h oplossen komt er
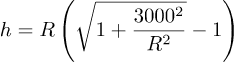
We zullen h zometeen uitrekenen maar eerst kijken we naar de wandeling van Zandvoort naar Scheveningen.
Eerst weer een plaatje

Nu weten we de lengte van het boogje, hier aangegeven met d. Voor de oplossing van het probleem is de hoek α ook van belang. Er geldt namelijk
![]()
en hieruit is h op te lossen:
![]()
De formules zien er inderdaad anders uit en beide kunnen makkelijk met (be)hulp van een rekenmachientje uitgewerkt worden. Voor R, de straal van de aarde, vullen we 40000000/(2π) m in (de omtrek van de aarde is namelijk per definitie 40000 km). Voor de hoogte van het uiteinde van de weg krijgen we iets meer dan 70 centimeter: 70,66479472 cm.
Mijn antwoord aan die lezer was dus: “Ja, het klopt.”
Margriet van der Heiden heeft er in haar rubriek Vormen en Getallen ook over geschreven:
NRC: 27-01-2017 (gedrukte versie: 28-01-2017).
Voor de wandeling van Zandvoort naar Scheveningen geldt dat de hoek α gelijk is aan d/R (we werken in radialen). Google maps geeft aan dat de wandeling van station Zandvoort naar de Pier van Scheveningen 38 km is, we nemen dus d=38000 m. Mijn rekenmachientje geeft aan dat we zo’n 113 m boven Scheveningen eindigen (113,4132864 volgens mijn rekenmachientje).
Morgen zullen we zien dat er minder verschil tussen de twee vragen zit als misschien lijkt, maar voor nu een paar opgaven.
Opgave 1: Als John Körmeling:de weg in zou (laten) graven hoe diep zou de weg dan in het midden liggen?
Opgave 2: Aangenomen dat het pad een meter breed wordt: hoeveel kubieke meter schelpen moet er aangevoerd worden?
Hoeveel grond zou weggegraven moeten worden bij de ingraafmethode?
Opgave 3: Bij de wandeling van Zandvoort naar Scheveningen is de afstand afgerond tot 38000 m.
Probeer andere waarden van d om te zien wat de invloed van die afronding op de hoogte is.
Vergroot/verklein d in stappen van 100 m bijvoorbeeld.
Eieren leggen
Hoeveel eieren zijn er nodig om een omelet om de aarde te bakken?
Vandaag (2017-06-12) in het economiekatern van De Volkskrant:
Elke dag leggen de 6,6 miljard legkippen op onze aardkloot een slordige
3 miljard eieren, genoeg op de hele planeet van antarctica tot de
Noordpool te verpakken in één luchtige reuzenomelet.
Eens even rekenen. De oppervlakte van de aarde is 4πR2, waarbij R de straal van de aarde is. Als we in (vierkante) meters willen rekenen dan geldt R=40000000/(2π).
Dat geeft, afgerond, een oppervlakte van 5,092958178×1014m2. Delen we dat door 3 miljard dan komen we uit op iets meer dan 169.765m2 per ei. Dat zou een vierkant van 412 bij 412 meter zijn.
Een XL ei uit de supermarkt verplaatst, inclusief schaal, 70 ml water. Onze omelet bestaat dus uit telkens 70cm3 ei, uitgesmeerd over die 169.765m2.
Na uitsmeren geeft dat een laag van wel 0,4×10-9 meter dik, zegt U maar 4 ångström.
Dat is een omelet van niks; om de aarde met een laag ei van 4mm dik te bestrijken, nog voor we gaan bakken, zullen we grofweg tien miljoen dagen moeten wachten — en met zijn allen geen enkel ei opeten.
Hieronder is de berekening te zien, uitgevoerd in Maple.

Berekening, alles uitgedrukt in meters.
Moeilijk bewijs(?)
Een paar weken geleden stond de volgende vraag op wisfaq.nl onder de titel Moeilijk bewijs.
Op een lijn zijn elf verschillende punten gegeven: P1,P2, …, P11. Voor elk tweetal punten geldt: de afstand tussen Pp en Pq is ten hoogste 1. Bewijs dat de som van alle (55) afstanden |PpPq| kleiner is dan 30.
Dat klinkt inderdaad moeilijk (55 afstanden niet groter dan 1 bij elkaar optellen en de som onder de 30 houden); tot je een plaatje tekent van alle elf punten van links naar rechts op die lijn. Voor die lijn kun je net zo goed de getallenlijn nemen en dan heb je elf getallen, P1,P2, …, P11 gerangschikt van klein naar groot (teken de situiatie maar even); De afstand tussen Pi en Pj is dan gewoon Pj-Pi als i<j. De situatie blijkt dan wat gunstiger: de grootste onderlinge afstand is P11-P1, de andere zijn kleiner (soms een stuk kleiner).
In groepen verdelen
Zo kun je bijvoorbeeld alle afstanden Pi+1-Pi voor i=1,2,…10 bij elkaar optellen en dat geeft P11-P1; toch mooi tien termen die samen niet meer dan 1 opleveren.
Vervolgens kunnen we alle afstanden Pi+2-Pi optellen, voor i=1,2,…,9. Dat doen we in twee groepen: voor de oneven i en voor de even i. We krijgen respectievelijk (P3-P1) + (P5-P3) + (P7-P5) + (P9-P7) + (P11-P9) = P11-P1 en (P4-P2) + (P6-P4) + (P8-P6) + (P10-P8) = P10-P2. De totale som is dus kleiner dan 2 (kleiner omdat P10-P2<1).
Als je de verschillen Pi+3-Pi gaat optellen, voor i=1,2,…,8, dan ontdek je dat je drie groepjes moet maken, elk met een som kleiner dan 1.
Bij de verschillen Pi+4-Pi krijg je vier groepen met een totale som kleiner dan 4.
Bij de verschillen Pi+5-Pi krijg je vijf groepen met een totale som kleiner dan 5.
Bij de verschillen Pi+6-Pi krijg je ook vijf groepen met een totale som kleiner dan 5: je krijg alleen P7-P1 tot en met P11-P5 omdat 6+6=12.
Dit loopt zo af, je krijg achtereenvolgens sommen die kleiner zijn dan 4, 3, en 2; aan het eind staat nog een keer P11-P1 en die is nioet groter dan 1.
Alles bij elkaar geteld is de totale som dus kleiner dan 1+2+3+4+5+5+4+3+2+1=30.
Kan het beter?
De 30 kan niet verbeterd: door P1 tot en met P6 heel dicht bij 0 te nemen en de rest van de punten heel dicht bij 1 kun je de totale som zo dicht bij 30 krijgen als je maar wilt.
Verder onderzoek
Probeer een formule op te stellen voor de kleinste bovengrens van de som van de ondelinge afstanden bij n punten.
Wat kunnen we zeggen als de punten in het vlak liggen? Alle ondelinge afstanden kleiner dan 1; hoe groot kan de som van die afstanden zijn?

Recent Comments