Posted in 2017
Eindexamen wiskunde B pilot, 2017
Ik heb ook naar het Eindexamen wiskunde B 2017 (pilot) gekeken om te zien wat de nieuwe wiskunde B ons biedt.
Mijn uitwerkingen zijn hier te vinden. Dit examen is `kaler’ dan dat van het gewone wiskunde B, in die zin dat bijna alle vragen contextloos zijn. Er was overeenkomst: de vraag over rakende grafieken en die over brandveilgheid komen in beide examens voor.
Ik kreeg wel het gevoel dat de leerling iets meer bij de hand genomen wordt: veel vragen zijn zeer gericht en geven informatie (zoals uniciteit en vorm van oplossingen, en figuren) die ook gaandeweg de oplossing door de leerling gevonden/gemaakt had kunnen zijn. Van mij hadden de vragen iets opener mogen zijn.
Eindexamen Wiskunde A, 2017
Na het examen Wiskunde B heb ik ook eens naar het examen Wiskunde A gekeken.
Het is lang geleden dat ik iets van dat vak had gezien; het is immers niet iets wat je in het pakket van een aankomende TU-student verwacht. Ik heb de indruk dat er meer leesvaardigheid wordt getest dan wiskundige vaardigheid. De meeste vragen bleken, na veel leeswerk, niet meer dan rekensommen, met exponentiele en logaritmische functies, dat wel. Bij de kansrekening/statistiekopgaven was het rekenwerk voor de rekenmachine.
De opgaven staan hier.
Mijn uitwerkingen, met commentaar, zijn hier te vinden.
Eindexamen Wiskunde B 2017
Het Eindexamen Wiskunde B van 2017 was gisteren, 15 mei. Ik heb het gemaakt.
Het examen is op examenblad.nl te vinden. Het examen test een redelijk aantal vaardigheden: e-macht, logaritme, gonio, integraal- en differentiaalrekening, en meetkunde.
Hier zijn mijn uitwerkingen
What is `Finite’?
What does `finite’ mean, mathematically?
In February I talked about this in our Lunch Colloquium; you can read the slides of that talk here.
Some time later the editors of Machazine, the journal of our student association Christiaan Huygens, asked me to write something `mathematical’ for them. I decided to expand my talk into a short article for them, it is available here, for your edification.
Een `wiskundig’ probleem (deel 2)
Naar aanleiding van allerlei reacties, op Twitter, op de vorige post een paar losse opmerkingen.
1. Sommigen gaven 13 als antwoord bij 5+8, met de rechtvaardiging dat de tweede en derde gelijkheden gewoon fout waren. Dat vind ik eigenlijk de verstandigste oplossing: als je + schrijft dan bedoel je kennelijk `optellen’; niet raar doen dus.
2. Het meest gegeven antwoord is 45 en de gedachtengang zal veelal iets geweest zijn als: de onderlinge verschillen zijn 7 en 9, dus van 3 naar 4 zal dat 11 zijn, van 4 naar 5 dan 13, en dat brengt ons 45 als uitkomst bij 5+8.
2a. Als alternatief kun je proberen te reconstrueren wat de nieuwe betekenis van + kan zijn; het meest voor de hand ligt `de som van m*n en m’ (niet m*n+m opschrijven want + betekent niet meer `optellen’), ook dat leidt tot 45.
2b. Wat minder mensen kwamen met 32: die oplossing slaat 4 over en gebruikt het verschil 11 om de volgende uitkomst te bepalen.
2c. Een ander populair antwoord is 34, met als uitleg “tel de echte waarde van de som op bij de vorige uitkomst”. Als je dit zou toepassen met inachtneming van de tussenstap 4+7 zou je weer op 45 uitkomen.
3. In het tijdschrift Pythagoras, in de nummers van april 2009 (De IQ-formule) en juni 2009 (IQ-formule light), is uitgelegd hoe je systematisch bij een eindig rijtje getallen een formule kunt maken die het rijtje voortzet. In tegenstelling tot wat de titels van de artikelen suggereren zul je het met deze formules bij een IQ-test niet goed doen omdat de formule geen rekening houdt met de gedachten van de opstellers.
4. De formule uit de vorige post, met als resultaat 5@8=4754660328285, is eigenlijk niet meer dan de methode uit Pythagoras, maar dan met heel ingewikkelde input.
5. In dit boek (pagina’s 344 en 345) wordt het rijtjes-voortzettings-probleem statistisch aangepakt. Met Bayesiaanse argumenten wordt voor twee potentiële verklaringen bekeken welke de meest waarschijnlijke is. Ook daar de waarschuwing dat het nooit 100% duidelijk zal zijn wat de opsteller van het probleem echt gedacht heeft.
Een `wiskundig’ probleem
Op internet doet de volgende opgave de ronde
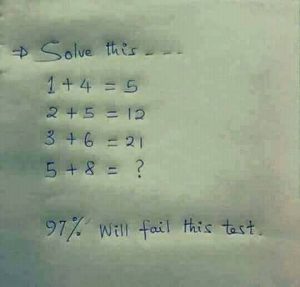
Ik ben persoonlijk geen fan van dit soort `sommen’ omdat de taak niet is te achterhalen wat *de* wetmatigheid achter de gegevens is, want een unieke wet is er niet, maar de wetmatigheid die in het hoofd van de opsteller zat. Mijn standaardantwoord is: 0 (of anders 42, het universele antwoord uit The Hitch-hikers Guide to the Galaxy).
Is er iets zinnigs over een opgave als deze te zeggen? Laten we eens kijken.
Om te beginnen: de + heeft duidelijk niet de functie van optelling. Dat bracht velen er toe het door een ander symbool te vervangen, @ bijvoorbeeld.
De vraag is dan: is er een bewerking @ die voor elk paar natuurlijke getallen m en n een natuurlijk getal m@n produceert en wel zo dat 1@4=5, 2@5=12 en 3@6=21? En zo ja, wat is dan 5@8?
Voor een wiskundige is het antwoord duidelijk: afgezien van die drie eisen kunnen we doen wat we willen, dus het antwoord is ja en 5@8 kan elk getal zijn.
Bijvoorbeeld: definieer m@n=0, behalve in de voorgeschreven drie gevallen; dat rechtvaardigt mijn standaardantwoord. Als we apart 5@8=42 definieren wordt het universele antwoord van Deep Thought correct.
De meeste mensen verwachten niet een antwoord als boven maar een *formule*; één of andere uitdrukking met m en n er in die `voorspelt’ wat 5@8 moet zijn. Dat soort formules zijn er te over.
Als je goed kijkt zijn de drie gegevens van de vorm m@(m+3)=x, dus het zou
kunnen dat de bewerking een flauwe is die alleen van de eerste coördinaat
afhangt.
Er zijn drie waarden gegeven en die kunnen met behulp van een kwadratische uitdrukking als functie van m alleen gegeven worden.
Ga maar na dat m@n=m*m+4m aan de drie eisen voldoet (vul m=1,2,3 in). Dat geeft het op internet meest gegeven antwoord op de vraag: 5@8=25+20=45.
Met een kleine truc kun je oneindig veel formules maken die aan de drie eisen voldoen, maar die voor 5@8 telkens een andere uitkomst opleveren. Die truc komt er op neer dat je iets maakt dat voor 1, 2, en 3 de waarde nul oplevert en voor andere natuurlijke getallen niet, bijvoorbeeld (m-1)(m-2)(m-3).
Nu kunnen we oneindig veel formules opschrijven die allemaal aan de gegevens voldoen maar die voor 5@8 telkens iets anders opleveren: neem een vaste k en definieer m@n=m*m+4m + k(m-1)(m-2)(m-3).
Met wat puzzelen zijn er vast formules te maken die voor 5@8 elke waarde kunnen produceren die je maar wilt; ik zou zeggen: aan het werk.
Hier is alvast een voorbeeld.
![]()
Deze geeft 5@8=4754660328285.
Voor wie wil weten of het rijtje 5, 12, 21 nog natuurlijke uitbreidingen heeft kan ik de On-line Encyclopedia of Integer Sequences aanbevelen: vul het rijtje in het zoekveld in om te zien wat er allemaal te vinden is.
A Pitch
Gisteren (2017-05-08) op de EWI-onderwijsdag een TEDx-achtige pitch gemaakt.
Dit is hem:
Op 29 november 1873 vroeg Georg Cantor aan Richard Dedekind:
“Zijn er evenveel natuurlijke getallen als reële getallen?”
Dedekind schreef in zijn dagboek dat hij dat maar een rare vraag vond.
Toch ging hij meedenken en samen stelden ze onder meer vast dat er evenveel
rationale getallen als natuurlijke getallen zijn.
Op 7 december 1873 kwam de doorbraak; Cantor schreef aan Dedekind:
“Er zijn meer reële getallen dan natuurlijke getallen.”
Omdat dit liet zien er van een ander, belangrijk, soort getallen ook meer
zijn dan natuurlijke getallen schreef Dedekind in zijn dagboek:
“Cantor heeft op magistrale wijze mijn twijfel weggenomen.”
Door duidelijk te maken wat `evenveel’ betekent en te laten zien dat er meer
dan één soort oneindig bestaat heeft Cantor de Wiskunde voorgoed
veranderd.

Recent Comments