Posted in June 2017
KP checkt: Ruim de helft meer …
Op twitter werd er al schande van gesproken: vandaag (2017-06-27) in NRC: … iets meer dan 100 Euro, ruim de helft meer dan de 46,45 Euro … (NRC Checkt).
Is 100 echt ruim de helft meer dan 46,45? Nee, natuurlijk niet. `Meer’ en `minder’ doe je altijd ten opzichte van het beginbedrag, en dat is hier 46,45. De helft van dat bedrag is 23,225 en `ruim de helft’ is wat subjectief, maar hoger dan 30 zou ik toch niet gaan. Ruim de helft meer dan 46.45 is dus niet meer dan ongeveer 76 a 77.
Ik beoordeel deze bewering van NRC Checkt als ONWAAR.
Overigens zie je zo waar dat `ruim de helft’ vandaan komt: 100 is inderdaad ruim de helft van 100 zelf (namelijk 53,55) meer dan 46.45. Hoe begrijpelijk ook, het is op zijn zachtst gezegd niet handig: het wordt snel onwerkbaar als je bij iedere transactie moet vragen of het om een deel van het begin- of van het eindbedrag gaat.
Om verwarring te voorkomen rekent men altijd vanuit het beginbedrag. In het stuk van NRC Checkt zou dat nog spectaculairder klinken: … iets meer dan 100 Euro, ruim het dubbele van de 46,45 Euro …

On-line is het al verbeterd, maar papier is geduldig.
Herkansing Wiskunde B, 2017
Gisteren was de herkansing Wiskunde B, zie hier voor de opgaven.
Hier is mijn uitwerking met wat opmerkingen.
Raaklijnen aan de aarde, II
Vandaag los ik een belofte van gisteren in door te laten zien wat de twee vragen van gisteren gemeen hebben, naast het feit dat beide iets met raaklijnen aan het aardoppervlak te maken hebben.
De vraag naar de hoogte van het eindpunt van de rechte weg van John Körmeling leidde tot de formule
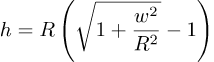
Gisteren stond er 3000 op de plaats van de w maar ik heb die w ingevoerd om de structuur van de formule duidelijk te maken. Ter herinnering R is de straal van de aarde.
De vraag over de wandeling van Zandvoort naar Scheveningen leidde tot
![]()
Hierin is α de hoek, in radialen, tussen de positievectoren (vanuit het middelpunt van de aarde) van Zandvoort en Scheveningen. Er geldt dat α=d/R, waar d de gelopen afstand is (gemeten langs het aardoppervlak natuurlijk).
Die formules lijken niet echt op elkaar maar voor een wiskundige met haast en zonder rekenmachine op zak zijn ze eigenlijk gelijk. Het punt is namelijk dat w/R en α erg klein zijn (en (w/R)2 nog kleiner). Voor kleine x gelden de volgende benaderingen.
![]()
en
![]()
Voor wie wat weet over Taylorpolynomen komen deze benaderingen niet als een verrassing. Voor wie die polynomen niet kent: de benadering van √(1+x) krijg je door je te realiseren dat (1+x/2)2=1+x+x2/4. Als x heel klein is is x2 nog veel kleiner en dat maakt de benadering goed genoeg. Voor de benadering van cos(x) zonder gebruik van de stelling van Taylor verwijs ik naar dit artikel in Pythagoras; daar wordt ook bekeken hoe goed die benadering eigenlijk is.
Als we de benaderingen gebruiken krijgen we de volgende benaderingen van de
twee hoogtes. Voor de weg:
![]()
Voor de hoogte aan het eind van de wandeling:
![]()
Voor deze laatste benadering doen we twee stappen: de teller wordt R×α2/2=d2/(2R). Nu moeten we nog met 1/(1-α2/2) vermenigvuldigen, maar voor kleine x geldt
![]()
dus vermenigvuldigen we met 1+α2/2 met als resultaat
![]()
Die laatste term is zo klein dat we hem weg mogen laten.
Als we de benaderingen toepassen krijgen we 0.706858347 voor de weg en 113.4114948 voor de wandeling. De verschillen met de antwoorden dan gisteren zijn in de orde van grootte van tienden van milimeters voor de weg en van milimeters voor de wandeling.
Waarom zou je die benaderingen maken? Een rekenmachientje geeft toch meteen een uitkomst, ook met de ingewikkelde formules? Het antwoord is tweeledig. Ten eerste heb je niet altijd een rekenmachine bij de hand en dat worden die formules wat bewerkelijk. Ten tweede, en dat is de eigenlijke reden: aan de benadering kun je vaak beter afzien hoe de uitkomst van de invoer afhangt. In beide gevallen hebben we gezien dat er een kwadratisch verband is: de grafiek van h als functie van w of d is nagenoeg een parabool.
Een ander voorbeeld van het werken met benaderingen is te vinden in dit artikel uit Pythagoras:
Een touwtje om de aarde.
Tot slot wat opdrachten.
Opgave 1. Bereken d4/(4R3); was het gerechtvaardigd die term weg te laten?
Opgave 2. Ga na dat de benadering ook werkt voor de diepte van de ingegraven weg.
Opgave 3. De benadering zijn, natuurlijk, niet exact. Ga na of ze de echte waarden over- of onderschatten (ook voor de ingegraven weg).
Opgave 4 Onderzoek hoe goed de benadering 1+x van 1/(1-x) is.
Raaklijnen aan de aarde, I
Zo af en toe kom ik een vraag tegen die opgelost kan worden door naar een raaklijn aan het aardoppervlak te kijken.
Op de website van De Ingenieur verscheen in januari een stuk over een project van de kunstenaar
John Körmeling: het aanleggen van een echt rechte weg. De bedoeling is dat de weg recht is in de zin van `een rechte lijn’: het wegoppervlak ligt dus in een raakvlak aan het aardoppervlak.
De weg van Körmeling (eigenlijk een schelpenpad) wordt zes kilometer lang, drie kilometer naar beide kanten vanuit het raakpunt. In het stuk wordt verteld dat de weg aan de uiteinden zo’n 70 centimeter boven het aardoppervlak komt te liggen. Ik kreeg van een lezer van Pythagoras de vraag of dat wel klopt; het leek wat weinig.
Op de wisfaq werd bijna hetzelfde gevraagd maar over iets grotere afstand: als ik van Zandvoort naar Scheveningen zou lopen over een rechte weg als die van Körmeling hoe hoog boven Scheveningen komt ik dan uit?
De vragen zijn bijna maar niet helemaal hetzelfde: bij de weg van Körmeling weten we hoe lang de rechte lijn zelf is, en bij de tweede vraag weten we de afstand langs het aardoppervlak. Dat heeft gevolgen voor de vorm van de oplossingen, zoals we zo dadelijk zullen zien.
Eerst een plaatje voor de rechte weg
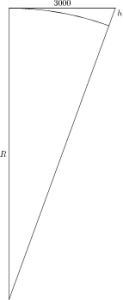
Hier is R de straal van de aarde en h de hoogte van het uiteinde van de weg boven het aardoppervlak. De stelling van Pythagoras brengt hier uitkomst: de onbekende h moet voldoen aan (R+h)2=R2+30002. Als we dit naar h oplossen komt er
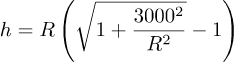
We zullen h zometeen uitrekenen maar eerst kijken we naar de wandeling van Zandvoort naar Scheveningen.
Eerst weer een plaatje
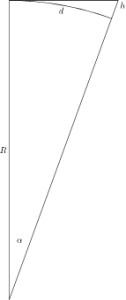
Nu weten we de lengte van het boogje, hier aangegeven met d. Voor de oplossing van het probleem is de hoek α ook van belang. Er geldt namelijk
![]()
en hieruit is h op te lossen:
![]()
De formules zien er inderdaad anders uit en beide kunnen makkelijk met (be)hulp van een rekenmachientje uitgewerkt worden. Voor R, de straal van de aarde, vullen we 40000000/(2π) m in (de omtrek van de aarde is namelijk per definitie 40000 km). Voor de hoogte van het uiteinde van de weg krijgen we iets meer dan 70 centimeter: 70,66479472 cm.
Mijn antwoord aan die lezer was dus: “Ja, het klopt.”
Margriet van der Heiden heeft er in haar rubriek Vormen en Getallen ook over geschreven:
NRC: 27-01-2017 (gedrukte versie: 28-01-2017).
Voor de wandeling van Zandvoort naar Scheveningen geldt dat de hoek α gelijk is aan d/R (we werken in radialen). Google maps geeft aan dat de wandeling van station Zandvoort naar de Pier van Scheveningen 38 km is, we nemen dus d=38000 m. Mijn rekenmachientje geeft aan dat we zo’n 113 m boven Scheveningen eindigen (113,4132864 volgens mijn rekenmachientje).
Morgen zullen we zien dat er minder verschil tussen de twee vragen zit als misschien lijkt, maar voor nu een paar opgaven.
Opgave 1: Als John Körmeling:de weg in zou (laten) graven hoe diep zou de weg dan in het midden liggen?
Opgave 2: Aangenomen dat het pad een meter breed wordt: hoeveel kubieke meter schelpen moet er aangevoerd worden?
Hoeveel grond zou weggegraven moeten worden bij de ingraafmethode?
Opgave 3: Bij de wandeling van Zandvoort naar Scheveningen is de afstand afgerond tot 38000 m.
Probeer andere waarden van d om te zien wat de invloed van die afronding op de hoogte is.
Vergroot/verklein d in stappen van 100 m bijvoorbeeld.
Eieren leggen
Hoeveel eieren zijn er nodig om een omelet om de aarde te bakken?
Vandaag (2017-06-12) in het economiekatern van De Volkskrant:
Elke dag leggen de 6,6 miljard legkippen op onze aardkloot een slordige
3 miljard eieren, genoeg op de hele planeet van antarctica tot de
Noordpool te verpakken in één luchtige reuzenomelet.
Eens even rekenen. De oppervlakte van de aarde is 4πR2, waarbij R de straal van de aarde is. Als we in (vierkante) meters willen rekenen dan geldt R=40000000/(2π).
Dat geeft, afgerond, een oppervlakte van 5,092958178×1014m2. Delen we dat door 3 miljard dan komen we uit op iets meer dan 169.765m2 per ei. Dat zou een vierkant van 412 bij 412 meter zijn.
Een XL ei uit de supermarkt verplaatst, inclusief schaal, 70 ml water. Onze omelet bestaat dus uit telkens 70cm3 ei, uitgesmeerd over die 169.765m2.
Na uitsmeren geeft dat een laag van wel 0,4×10-9 meter dik, zegt U maar 4 ångström.
Dat is een omelet van niks; om de aarde met een laag ei van 4mm dik te bestrijken, nog voor we gaan bakken, zullen we grofweg tien miljoen dagen moeten wachten — en met zijn allen geen enkel ei opeten.
Hieronder is de berekening te zien, uitgevoerd in Maple.
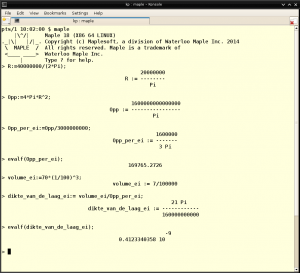
Berekening, alles uitgedrukt in meters.

Recent Comments