Posts in category taal

We gaan het artikel Sets and Sentences van D. Terrence Langendoen en Paul Postal opnieuw lezen. De vorige keer heb ik de inhoud beschreven; nu bekijken we die nogmaals, maar met een wiskundig oog.

Zoals vorige keer beschreven gaat het er in het artikel om te laten zien dat in een Natuurlijke Taal de mogelijke zinnen een zeer grote collectie vormen: te groot om `verzameling’ genoemd te mogen worden. We volgen de redenering stap voor stap.

De definitie van Co-ordinate compound constituent is vorige keer al schematisch weergegeven door het volgende plaatje:

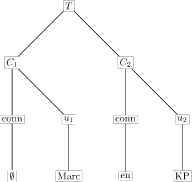
De top T is hier de co-ordinate compound constituent en de andere knopen zijn de conjucten waar T uit gevormd is. Die conjuncten bestaan uit een connectief en `constituent’. Ietwat simplistisch: T ontstaat door de constituents door middel van connectieven aan elkaar te plakken.

In punt (6) van het artikel wordt gedetailleerd beschreven hoe dat plakken in zijjn werk moet gaan, of preciezer: er wordt geformuleerd wat de relatie tussen de verzameling U van constituents en de compound T moet zijn. Uit die formulering zou je een plakmethode kunnen distilleren. Van punt (6) citeer ik deelpunt (d)

if two elements of U occur as subconjuncts of conjuncts C₁ and C₂ of T then C₁ and C₂ occur in a fixed order. Where C₁ and C₂ are of distinct length assume the shorter precedes; where C₁ and C₂ are the same length, assume some arbitrary order.

Als een student zoiets opschrijft trek ik mijn rode pen: ten eerste om het gebruik van `fixed’ en `arbitrary’ vlak achter elkaar, en ten tweede om dat `arbitrary’. Dat lees ik als “doe maar wat” en daar schrijf ik dus “Hoe dan?” bij. Ik kom straks nog op dit punt terug.
Verder in punt (6) wordt T een `co-ordinate projection’ van U genoemd en U de `projection set’ van U. Inderdaad: U is door T uniek bepaald maar niet andersom; het woord `arbitrary’ lijkt daar op te duiden.

Dan volgt een alinea waarin wordt beargumenteerd dat elke verzameling U een co-ordinate projection heeft. Dit zou `straightforward’ moeten zijn, volgens de schrijvers althans. Hier zijn de stappen (de `category Q’ die ter sprake komt is een niet nader gespecificeerde abstracte categorie van zinnen):

1. Neem een verzameling U en laat k de kardinaliteit van U zijn (eindig of oneindig)
2. Citaat: Clearly, from the purely formal point of view, there is a co-ordinate compound W belonging to the category Q. Dat klinkt mooi maar het heeft geen enkele bewijskracht; geen enkele rechtvaardiging, geen indicatie waar die W vandaan zou moeten komen.
3. Citaat: Since there are no size restrictions on co-ordinate compounds, W can have any number, finite (more than one) or transfinite of immediate constituents. Dit is slechte (wiskundige) stijl: eerst lijkt W vast, dan gaat hij alsnog variëren. Een betere formulering zou zijn: “er zijn co-ordinate compounds van alle mogelijke kardinaliteiten”. Die betere formulering maakt de bewering niet automatisch waar, er is nog steeds geen concrete rechtvaardiging gegeven.
4. Citaat: W can then, in particular have exactly k such constituents. Nogmaals: die vaste W is omgevormd tot een gepaste W. Niet mooi, maar vooruit dan maar.
5. De deelconjuncts van de conjuncts in W vormen een verzameling V die, volgens de regels in (6), kardinaliteit k heeft. Niks mis mee.
6. Citaat: To show that W is a co-ordinate projection of U, it then in effect suffices that there exist a one-to-one mapping from U to V. Niet dus. Hoe je definitie (6) ook wendt of keert, dit haal je er niet uit. Wil W een co-ordinate projection van U zijn dan zal de verzameling V exact gelijk aan de verzameling U moeten zijn; een bijectieve afbeelding tussen die twee is echt niet genoeg.
7. Citaat: But this is trivial, since the two sets have the same number of elements. Dit klopt, maar ik verdenk de schrijvers ervan dat ze niet doorhebben wat hier achter zit. Georg Cantor definieerde `kardinaliteit’ op een manier die eigenlijk nietszeggend is, zie de tweede post in deze serie. Hij bewees daarna dat `hebben gelijke kardinaliteit’ equivalent is met `er bestaat een bijectieve afbeelding tussen’, maar tegenwoordig is dat laatste de definitie van het eerste.

Afsluiting

In het artikel formuleren Langendoen en Postal nu een afsluitingsprincipe. Na een waarschuwing dat niet elke co-ordinate projection noodzakelijkerwijs welgevormd is komt het volgende Closure Principle for Co-ordinate Compounding:
If U is a set of constituents each belonging to the collection, S_w, of (well-formed) constituents of category Q of any natural language, then S_w contains the co-ordinate projection of U.
Hoezo “the co-ordinate projection”? Uniciteit van die projecties is nog niet aan de orde geweest en over die collectie S_w is niet (expliciet) gezegd dat elke verzameling zinnen maar op één manier tot een grotere zin samen te voegen is.

Na een opmerking over het recursieve karakter van dit principe noemen de schrijvers de categorie S van zinnen als een categorie waarop het principe van toepassing is, althans: ze beweren dat (maar geven geen bewijs).
Dat weerhoudt ze er niet van het principe twee keer uit te spreken voor S. Eerst via een bijna letterlijke herhaling, met Q vervangen door S, en dan nog een keer met behulp van een formule(!): the co-ordinate projection van een verzameling U noteren we CP(U) en dan krijgen we

(∀U)(U⊂L → CP(U)∈L)

Hierin is L de collectie van alle elementen van de categorie S van een natuurlijke taal (voor mij betekent dat L=S want L en S hebben dezelfde elementen, maar er is misschien een subtiel verschil tussen de collectie van elementen van een categorie en de categorie zelf). Merk op dat hier het onbepaalde lidwoord definitief bepaald geworden is. Zonder het expliciet uit te spreken hebben de schrijvers kennelijk besloten dat compounding maar op één manier kan; de functienotatie CP(U) kan niet anders geïnterpreteerd worden.

Maar hoe is CP(U) gedefinieerd dan? Dat wordt niet duidelijk; een illustratie met met verzamelingen van drie, vier zinnen die tot één worden samengevoegd overtuigt mij niet.

Een soort van hierarchie

Dan komt eindelijk datgene waar ik al lang op zat te wachten: The Cantorian Analogue, waarin bewezen gaat worden dat de zinnen in een natuurlijke taal geen verzameling vormen. Overigens, een definitie van `verzameling’ hebben we nog niet echt gehad.

Het bewijs gaat aanvankelijk met gebruik van een verzameling zinnen als in de vorige post, de schrijvers gebruiken {Babar is happy; I know that Babar is happy; I know that I know that Babar is happy, …}. Die verzameling noemen ze S₀.
Ik kort de zinnen even af: z₀ is “Babar is happy” en, gegeven z_n is z_n+1 de zin “I know that z_n“.
Onder de aanname dat de natuurlijke taal L aan het afsluitingsprincipe voldoet omvat L ook de verzameling S₁ die bestaat uit S₀ en de co-ordinate projections van de deelverzamelingen van S₀ met twee of meer elementen. De formulering verdient het nauwkeurig gelezen te worden.
Then L also contains a set S₁, made up of all the sentences of S₀ together with all and only the co-ordinate projections of every subset of S₀ with at least two elemente, that is, with a set containing one co-ordinate projection for each member of the power set of S₀ whose cardinality is at least 2.
Deze zin deugt niet. De delen voor en na `that is’ spreken elkaar tegen. De eerste versie van S<sub>1</sub> bevat alle co-ordinate projections van alle deelverzamelingen van S<sub>0</sub> — de projecties van iedere deelverzameling —; de tweede versie bevat van elke deelverzameling (precies) één projectie. Daarnaast is de eerste versie uniek bepaald door het `all and only’, daar is `the set S<sub>1</sub>‘ dus meer op zijn plaats; in het tweede deel past `a set’ wel.

Je zou het meervoud `projections’ enkelvoud kunnen maken; dat sluit wat beter aan bij de formulering van de afsluitingeigenschap, the projection zou dan telkens de functiewaarde CP(U) kunnen zijn. Maar dan gaat het ook mis: vóór het `that is’ is de keuze van projectie duidelijk vastgelegd, maar na `that is’ zit er nog potentiële willekeur in de keuze van projectie, er staat niet expliciet dat die one projection ook echt CP(U) is.

De schrijvers geven dan een voorbeeld van hoe S₁ er uit zou kunnen zien (dus toch geen welbepaalde verzameling):
{z₀; z₁; z₂; …; z₀ and z₁; z₀ and z₂; …; z₀, z₁, and z₂ …} (voor alle duidelijkheid: de punt-komma’s scheiden de zinnen en de komma’s dienen als connectieven in de zinnen).

Dan volgt een lange alinea waarin met veel omhaal van woorden de kardinaliteit van S₁ wordt bepaald. Door het `één projectie per verzameling’ is dat niet moeilijk: dat is dezelfde kardinaliteit als die van de familie van alle deelverzamelingen van S₀ en omdat S₀ aftelbaar oneindig is, en dus kardinaliteit ℵ₀ (alef-nul) heeft is die kardinaliteit gelijk aan 2^ℵ₀ (2-tot-de-macht-alef-nul) en niet ℵ₁, zoals Langendoen en Postal opschrijven. Ergens bij hun bestudering van de verzamelingenleer is er iets misgegaan en is de Continuümhypothese waar geworden.

Zoals wellicht verwacht wordt dit proces voortgezet. Er komt een rij verzamelingen S₀, S₁, S₂, …, netjes recursief gedefinieerd door S_n+1=S_n∪K_n. Hierbij is K_n telkens de verzameling projecties van deelverzamelingen van S_n. In formule

K_n={x:(∃y)(y⊆S_n ∧ x is the co-ordinate projection of y)}

Hier had dus ook K_n={x:(∃y)(y⊆S_n ∧ x=CP(y))} kunnen staan.

Op deze manier komt er een hierarchie van verzamelingen zinnen tot stand; die zinnen worden steeds complexer en de verzamelingen steeds groter. De schrijvers claimen onterecht dat voor elke n het kardinaalgetal van S_n gelijk is aan ℵ_n. De juiste formule is een machtsverheffing met een torentje van n tweeën, met bovenaan nog een ℵ₀. Dat kardinaalgetal noteren we in de verzamelingenleer als ℶ_n (beth-n).

Dit verhaal culmineert in wat de schrijvers The NL Vastness Theorem noemen: Natural Languages are not sets.
Het bewijs verloopt uit het ongerijmde. Neem aan dat L een verzameling is. Het proces van co-ordinate projection definieert een injectieve afbeelding van de machtsverzameling van L naar L zelf. Dat kan niet volgens een stelling van Cantor: elke verzameling heeft strikt meer deelverzamelingen dan elementen. Tegenspraak.

Er is echter een groot MAAR, en daar gaan we het nu over hebben.

Ordeningen en lengten

Het `bewijs’ in het artikel staat vol met impliciete aannamen over het gedrag van verzamelingen die een niet-wiskundige waarschijnlijk niet zo snel zullen opvallen. Er zijn twee dingen die nogal schadelijk zijn voor de redenering zoals hierboven beschreven.

Ten eerste de ordening, ik heb er bij de beschrijving van de co-ordinate projection al op gezinspeeld: daar zit, op zijn zachtst gezegd, een onvolledigheid.
Die onvolledigheid duikt op bij de overgang van S₁ naar S₂, en nog erger bij de stap daarna van S₂ naar S₃.
Bij de eerste stap, van S₀ naar S₁, is er niets aan de hand: we hebben onze verzameling S₀ genummerd en die nummering ordent elke deelverzameling van S₀, waarmee zo’n deelverzameling een natuurlijke projectie heeft, ook als deze oneindig veel elementen heeft. Dit levert natuurlijk wel zinnen zonder einde op.

Daarna, van S₁ naar S₂, hebben we een probleem: er zijn (overaftelbaar) veel zinnen van oneindige lengte (allemaal even lang als de verzameling der natuurlijke getallen). Daar gaat het `fixed’ en `arbitrary’ van punt (6)(d) dus wringen. Hoe orden je zo’n verzameling zinnen? De heren Langendoen en Postal spreken zich daar niet over uit.

Gelukkig kunnen we hier de lexicografische ordening gebruiken: kijk naar het eerste teken (inclusief spaties) waar de zinnen verschillen en neem een besluit op basis van de ordening van de tekens. Zie ook de post Boekenplanken voor gevorderden waar een aspect van die ordening aan de orde komt dat hier de zaak ook compliceert: er zijn heel veel verzamelingen die de eigenschap hebben dat tussen elk tweetal zinnen oneindig veel zinnen staan en die ook geen eerste zin hebben. Als we die ordening gebruiken om projecties te maken dan krijgen we dus zinnen zonder begin, zonder einde, en met voegwoorden die gaan ten minste één kant niet zien wat ze verbinden.

Het kan nog erger. We kunnen de verzameling S₂ opvatten als de familie van alle deelverzamelingen van de reële rechte R. En op die familie kan geen lineaire ordening gedefinieerd worden. Het sleutelbegrip is hier `definiëren’: er is geen formule die de familie deelverzamelingen van R zó sorteert dat elk tweetal verzamelingen vergelijkbaar is. De stap van S₂ naar S₃ kan eigenlijk niet genomen worden.

Ten tweede is er nog het begrip lengte van een zin. Cantor heeft een hele theorie van orde-typen (`lengten’) van lineair geordende verzamelingen ontwikkeld. Wat daar vooral opvalt is dat er veel onvergelijkbare orde-typen zijn. En die kom je ook tegen bij de stap van S<sub>2</sub> naar S<sub>3</sub>: het voorsorteren op `lengte’ gaat dus ook al niet.

Welordeningen?

“Maar, er zijn toch welordeningen?”, hoor ik degenen die wat verzamelingenleer hebben bestudeerd opwerpen. Dat klopt, en we hebben ook nog Zermelo’s Welordeningsstelling, die zegt dat elke verzameling een welordening heeft. Bij een welordening zijn de elementen zo gesorteert dat elke deelverzameling (niet-leeg) een eerste element heeft. Welordeningen zijn ook nog onderling vergelijkbaar, dus die co-ordinate projections schrijf je zo op.
Inderdaad, maar die welordeningsstelling is equivalent met het Keuzeaxioma en daarmee hoogst niet-constructief. Zoals de verzameling S₂ geen definieerbare lineaire ordening heeft heeft S₁ geen definieerbare welordening.
Je kunt met welordeningen werken maar dan laat je de willekeur van het Keuzeaxioma binnen en daarmee ben elke zweem van een grammatica kwijt.

Ik weet niet of je dan nog van een natuurlijke taal kunt spreken.

Korte samenvatting

We zijn hier nog niet aan het einde van het artikel Sets and Sentences gekomen. Er gebeurt wiskundig niet veel nieuws meer en het derde deel beargumenteerd dat zo ongeveer alle theoriën over natuurlijke getallen uit de tijd van schrijven niet deug(d)en. De argumenten steunen op The NL Vastness Theorem.
In het bewijs van die stelling zitten gaten. En die gaten bestaan vooral uit ontbrekende definities en aannamen.

Zo wordt nergens echt vastgelegd wat een verzameling eigenlijk is; het dichtst bij een definitie komt men in het bewijs van de Vastness Theorem: het kenmerkende van een verzameling is dat deze een kardinaliteit, een `aantal elementen’, heeft. Dat is de omgekeerde wereld en ook niet echt nodig.
Cantor definieerde eerst `Menge’ en pas daarna `Machtigkeit’; naar moderne maatstaven hebben die definities weinig inhoud maar ze stuurden de intuïtie wel de goede kant op.
De manier waarop ik het `bewijs’ van de stelling heb opgeschreven laat zien dat die aanname over kardinaliteit vermeden kan worden; we hebben alleen goede afspraken over het hebben van meer, minder en evenveel elementen nodig en dat kan zonder die aantallen te definiëren of benoemen. Net als we geen eenheid van lengte nodig hebben om uit te maken of ik langer, korter, of even lang ben als Marc van Oostendorp: zet ons naast elkaar en je weet het.

Zoals al opgemerkt zijn de centrale noties van het artikel niet goed afgesproken; de definities lijken, gezien de gegeven voorbeelden, vooral ingegeven door de eindige situatie. Bij het suggestief opschrijven van de verzameling S₁ zien we ook alleen maar eindige zinnen.
Ik vermoed dat niemand de schrijvers heeft gevraagd hoe men het zich moet voorstellen: een collectie zinnen die geordend is als de rationale getallen: zonder begin, zonder eind en met tussen elk tweetal zinnen ondindig veel andere. Hoe maak je daar een goedlopende zin van?