Posted in October 2019
Getallen bestaan (eigenlijk) niet
Dit is de derde in een korte serie blogposts naar aanleiding van een discussie op twitter over dit stuk op Neerlandistiek.nl van Marc van Oostendorp dat zelf weer een rectaie op dit artikel van Paul Postal was. De eerdere delen staan hier en hier.
Tussen al die tweets maakte ik de volgende opmerkingen:
Daar komt nog bij dat `getal' als aantal’ strikt genomen gedefinieerd moet worden; verzamelingen hebben geen intrinsiek `aantal elementen'. Boeken zijn inderdaad eerder stellingen. https://t.co/Mjjth2qDKd
— (((K P Hart))) (@hartkp) October 15, 2019
Daar wil ik het vandaag even over hebben. Wat zijn getallen eigenlijk? Die vraag werd zelfs op de Nationale Wetenschapsagenda gesteld en ik heb daar al eens een antwoord op gegeven. Ik wil dat hier wat uitgebreider doen.
Getallen
Om te beginnen: in de discussie en de stukken ging het over natuurlijke getallen en die werden vereenzelvigd met hun decimale schrijfwijze. Dat is, in deze tijd, heel natuurlijk: afgezien van jaartallen in Romeinse notatie op gevels van gebouwen (en als paginanummers in boeken vóór de echte inhoud begint) zien we getallen eigenlijk alleen opgeschreven met behulp van de indo-arabische cijfers en de positionele schrijfwijze.
Gegeven deze vereenzelviging is er wel iets te zeggen voor het idee dat boeken en getallen iets gemeen hebben: rijen symbolen met een welgedefinieerde inhoud.
Aan de andere kant: getallen zijn in zekere zin absoluut: ze zijn bestand tegen vertalingen. Twaalf, twelve, douze, tolv, dvanást’, teyan-a-bub, … verwijzen allemaal naar exact dezelfde hoeveelheid streepjes: ||||||||||||.
Als ik een stuk tekst van mezelf in het Engels vertaal is die exactheid weg. Sommige nederlandse woorden en uitdrukkingen doen het niet zo goed in letterlijke vertaling (“laat maar” versus “let but”) en een equivalent-bij-benadering is slechts dat: een benadering. Vergelijk deze twee stukken over de Gulden Snede maar: nederlands versus engels.
Meer, minder, even veel
Maar goed, terug naar de vraag over de aard, of het bestaan, van getallen. Ik denk/vind dat getallen, in de zin van aantallen, niet bestaan.
“Maar we tellen toch dagelijks dingen”, hoor ik u zeggen. Inderdaad, maar de zaken die we daarbij gebruiken zijn bedacht, ze bestaan niet in het wild. Ooit `het getal dat wij in het Nederlands drie noemen’ gezien? En hierbij wel de gebruikelijke notaties loslaten, het symbool 3 telt niet, en III ook niet, en γ’ ook niet.
Maar er is meer: in de verzamelingenleer is het na invoering van de bekende soorten afbeeldingen, injectief, surjectie, en bijectie een koud kunstje te definiëren wanneer de ene verzameling minder, meer, of even veel elementen heeft als een andere. Kleine kinderen weten dat al heel snel, en zonder tellen: haal uit beider zakje snoepjes telkens tegelijkertijd één snoepje. Het zakje dat het eerst leeg is bevatte minder snoepjes dan het andere en gelijk leegraken betekent even veel. Probeer het zelf maar eens: neem twee lepels hagelslag en zoek zo uit welke lepel de meeste korrels heeft.
Maar als je in de verzamelingen een antwoord wilt geven op de vraag “Hoeveel elementen?” sta je in het begin met de mond vol tanden. Na vrij veel werk lukt het een klasse van standaardverzamelingen af te zonderen waarmee andere verzamelingen gemeten kunnen worden en zo een `aantal elementen’ opgeplakt kunnen krijgen. Dat wil zeggen: dit werkt voor eindige verzamelingen, waarbij `eindig’ zo wordt gedefinieerd dat `het’ ook inderdaad werkt.
Hoeveel?
Hoe zit het met willekeurige verzamelingen? Georg Cantor dacht dat er zoiets als `het aantal elementen’ moest zijn; hij had zelfs een definitie:
,Mächtigkeit` oder ,Cardinalzahl` von M nennen wir den Allgemeinbegriff, welcher mit Hülfe unseres activen Denkvermögens dadurch aus der Menge M hervorgeht, dass von der Beschaffenheit ihrer verschiedenen Elemente m und von der Ordnung ihres Gegebenseins abstrahirt wird.
Uit die definitie halen we de volgende eisen waar dat Kardinaalgetal C(M) aan zou moeten voldoen:
- M en C(M) hebben even veel elementen (als bij de zakjes snoep), in vaktaal: er is een bijectie tussen M en C(M) — C(M) is dus ook een verzameling
- als er tussen M en N een bijectie bestaan dan C(M)=C(N)
Als er dus zo’n functie is dan kunnen we C(M) `het aantal elementen’ van M noemen.
En, helaas, zo’n functie kun je niet definiëren. Het bewijs van die ondefinieerbaarheid hoop ik maandag 16 december tijdens het laatste college van de Mastermath-cursus Set Theory af te ronden.
Wat betekent dit? Dat verzamelingen geen `intrinsiek’ aantal elementen hebben. Je kunt niet meer doen dan zelf een hoeveelheid standaardverzamelingen af te spreken waarmee je op zinvolle wijze betekenis aan `het aantal elementen’ kunt geven. Getallen zijn geen natuurverschijnselen maar mensenwerk.
Dit gebeurde vaker
De vraag wie van twee mensen langer of korter is is zo beantwoord: hou ze tegen elkaar aan en je ziet het. Om de vraag “Hoe lang zijn die twee mensen?” te beantwoorden zijn in de loop der tijd veel systemen bedacht, sommigen wat logischer dan de andere. Ons metrieke stelsel is overgebleven, ongetwijfeld door de voor de hand liggende definitie van de meter: neem de halve meridiaan van de noordpool door Parijs naar de evenaar en hak die in 10.000.000 even grote stukjes; elk stukje is, per definitie, één meter lang.
Oh, en `teyan-a-bub’? Dat gebruik je bij het tellen van schapen in Weardale.
De Gulden Onzin
Hier is weer wat flauwekul over de Gulden Snede.
Boekenplanken voor gevorderden
In dit vervolg op deze blogpost ga ik het hebben over het ordenen van boeken.
Bij de twitterdiscussie over of er verschil is, of niet, tussen boeken en getallen kwam ook de mogelijkheid getallen en boeken te ordenen ter sprake. Hierbij werd met `getal’ stilzwijgend `natuurlijk getal’ bedoeld. Nu komen natuurlijke getallen met een natuurlijke ordening, waarin elk getal een directe opvolger heeft en elk getal, behalve het eerste, een directe voorganger.
Hoe zit het met de boeken? Als je het met Marc eens bent dat een boek van vijf miljard pagina’s meer dan genoeg is zijn we gauw klaar.
Nee, ik denk dat het redelijk is om te zeggen dat een boek een bepaalde maximale omvang heeft: iets van vijf miljard pagina's is niet langer een boek, maar een serie boeken.
— Marc van Oostendorp (@fonolog) October 15, 2019
Als we het aantal bladzijden begrenzen en niet raar doen met onhandelbaar grote pagina’s en ook niet al te kleine letters gebruiken dan is, in een vaste alfabet, het aantal boeken eindig. Als we de letters, spaties, interpunctie etc van een vaste ordening voorzien kunnen we elk boek als een rij symbolen beschouwen en gewoon lexicografisch ordenen: als rij/boek A een echt beginstuk van rij/boek B is dan komt boek A voor boek B; anders kijken we naar de eerste plek waar A en B verschillen en gebruiken de ordening van de tekens om te beslissen welke van de twee eerst komt. Het resultaat is een rij boeken met een eerste en een laatste, waarin elk boek behalve het eerste een directe opvolger heeft, en elk boek behalve het laatste een directe voorganger.
En dit laat inderdaad een praktisch verschil zien tussen getallen en boeken: van de laatste zijn er maar eindig veel.
Oneindig veel boeken
Echter, …, de hele discussie begon met een artikel van Paul Postal, waarin het begrip boek wat ruimer werd opgevat: elke eindige rij symbolen is een potentieel boek.
Dan wordt het ordenen van de boeken een minder eenvoudige klus. Er was een heel specifieke vraag van Marc:
Maar boeken kun je toch ook ordenen? Bijvoorbeeld alfabetisch (op de hele tekst)? Dus na een boek dat eindigt op 'vrede op aardbei' komt een boek dat verder identiek is, maar eindigt op 'vrede op aarde'?
— Marc van Oostendorp (@fonolog) October 15, 2019
Het antwoord daarop is niet geheel flauw.
Lexicografisch
Je kunt je (potentiële) boeken nog steeds als hierboven lexicografisch ordenen. Dan is in ieder geval duidelijk dat het antwoord op de vraag van Marc bevestigend luidt: zijn twee boeken zijn geen beginstukken van elkaar en ze verschillen als eerste bij de positie van de b en de d, en de b komt voor de d. Er zitten natuurlijk nog zat boeken tussen die twee: aardbei komt voor aardbeienjam en dat komt voor aardappel hetwelk zelf weer voor aarde komt.
Het interessante, zeker voor wiskundigen, is dat tussen elk tweetal boeken oneindig veel (potentiële) boeken staan.
Tussen de nogal flauwe boeken (a) en (b) staan (ab), (aab), (aaab), (aaaab), … (een dalende rij boeken); tussen (ab) en (aab) kun je ook zoiets maken: (aba), (abab), (abaab), …
Dit is voor makers van boekeplanken nogal vervelend: de planken moeten overal oneindig lang zijn om al die oneindig veel tussenliggende boeken kwijt te kunnen.
Iets praktischer
Het kan praktischer (ook al door Marc opgemerkt in een commentaar op neerlandistiek.nl: sorteer de boeken eerst op lengte en orden ze bij vaste lengte weer gewoon lexicografisch. Dan heb je een eerste boek en elk ander boek heeft net als bij de natuurlijke getallen een directe voorganger en een directe opvolger. Dit is wel zo praktisch voor de timmerlieden: terwijl jij de planken vult kunnen zij gewoon vooruit werken.
Het verschil met hierboven is wel dat het aarde-boek van Marc vóóor het aardbei-boek komt: het eerste is één karakter korter dan het tweede.
Kleene-Brouwer
Tijdens de discussie noemde ik nog de Kleene-Brouwerorde; die lijkt op de lexicografische met dit verschil dat indien A een echt beginstuk van B is A juist achter B geplaatst wordt. Het tweede deel van de definitie blijft ongewijzigd. Dus (a) komt nog steeds voor (b), maar (aaa) komt voor (aa) en die weer voor (a).
Ook dit is een nachtmerrie voor boekenkastmakers: tussen elk tweetal boeken hebben we weer oneindig veel boeken. Het is zelfs een dubbele nachtmerrie: lexicografisch is er tenminste een eerste boek, bij Kleene-Brouwer hebben we dat niet eens; de timmerlieden moeten nu twee kanten op planken ophangen die overal oneindig veel boeken moeten kunnen hebben.
Voor mensen die werken in Beschrijvende Verzamelingenleer en in de Recursietheorie is de Kleene-Brouwerordening heel nuttig. Maar dat is weer een heel ander verhaal.
Boeken, getallen, stellingen
Vorige week ontspon zich een kleine discussie op Twitter over boeken en getallen; Marc van Oostendorp schreef Neerlandistiek.nl over een artikel van Paul Postal waarin de laatste over de aard, de ontologie, van boeken schrijft.
Boeken zijn als getallen. https://t.co/UPA1zENKqx
— Marc van Oostendorp (@fonolog) October 15, 2019
Ietwat kort door de bocht is de these van Postal dat een boek (hij gebruikte Pride and Prejudice als voorbeeld, Marc nam De Kleine Johannes als voorbeeld) als abstract object altijd al bestaan heeft, het is namelijk een rij symbolen (letters, spaties, interpunctie, …) en iemand heeft die rij een keer voor het eerst opgeschreven. Net als het getal gerepresenteerd door 7.987.923.892.274 (gezien de ene hit bij Google waarschijnlijk door Marc als eerste opgeschreven).
Voor het geval de ingebedde tweet hierboven niet goed werkt is hier een korte samenvatting van de discussie.
Mogelijke tegenwerping (Ionica Smeets): elk natuurlijk getal heeft een natuurlijke opvolger, hoe zit dat met boeken? Lijken boeken en stellingen niet meer op elkaar?
Antwoord (Marc): orden ze alfabetisch.
Ander argument (ik): dat werkt niet helemaal, als je alfabetisch wilt werken is Kleene-Brouwerorde beter, maar dan staan tussen elk tweetal boeken weer oneindig veel boeken (ik zag elke rij symbolen als een potentieel boek). Dit geldt overigens ook voor de normale Lexicografische orde van eindige rijen symbolen.
Antwoord (Marc): een boek van vijf miljard pagina’s is lang genoeg. Zou het verschil dan niet zijn dat er maar eindig veel boeken (kunnen) zijn?
Het laatste argument schuurt dan weer met de inhoud van het artikel van Postal (pagina 12): die laat willekeurig lange zinnen toe en concludeert dan dat er niet alleen oneindig veel boeken zijn maar zelfs overaftelbaar veel. Sterker nog: de boeken in een gegeven taal vormen niet eens een verzameling (volgens mij is dat laatste lariekoek maar daar hebben we het later nog wel eens over).
Is er wel verschil?
Je kunt op diverse niveau’s naar deze vraag kijken.
Representaties: rijen symbolen
Als het om opgeschreven verhalen en opgeschreven getallen gaat dan is er inderdaad geen echt verschil: beide bestaan uit rijen symbolen die hun betekenis prijsgeven als je volgens bepaalde regels (in dit geval op school aangeleerd) decodeert.
Bestonden die rijen symbolen ook al voor ze werden opgeschreven? En zo ja, hoe lang al?
Dat is een lastige vraag en waarschijnlijk voer voor lange filosofische discussies. Mijn mening: eigenlijk wel. In ieder geval sinds halverwege de negentiende eeuw (dat maakt het voor Pride and Prejudice wat onzeker): toen begon men namelijk functies als objecten te beschouwen en niet als `formules’ of `regels’. En Cantor nam, gegeven twee verzamelingen X en Y, de verzameling van alle functies van X naar Y ter hand om machtsverheffen van kardinaalgetallen te definiëren.
Als we dus voor een groot genoeg natuurlijk getal N alle functies nemen van {1,2,…,N} naar ons alfabet, aangevuld met spaties en interpunctiesymbolen, dan zit daar het verhaal van De Kleine Johannes (1884) dus ook in. In de tijd van Pride and Prejudice was de wiskunde nog niet zo ver en ik laat het aan de meer filosofisch ingestelden onder ons om te overdenken of dat boek er (ver) voor 1811 ook al was.
Het boek zelf; het getal zelf
Tot nu toe hebben we boek en getal vereenzelvigd met hun representaties. Bij een boek is dat bijna noodzakelijk. We kunnen het boek anders representeren, denk aan een lange rij nullen en enen in een e-reader, maar we hebben bij het lezen toch de oorspronkelijke rij symbolen nodig (tenzij iemand zich heeft aangeleerd de binaire code uit het hoofd te vertalen maar dat lijkt me vergezocht).
Bij een getal is dat niet zo. Neem het getal gegeven in decimale representatie als 1729 (decimale representatie) of als 6C1 (hexadecimaal) of als 11011000001 (binair). Deze representeren alledrie exact dezelfde hoeveelheid stippen, of hoop kogeltjes. En die hoop kogeltjes is de kleinste die op twee verschillende manieren in drie hoopjes verdeeld kan worden die dan elk als kubus gestapeld kunnen worden.
En Stellingen?
Ik was het in eerste instantie met Ionica eens maar nu twijfel ik. Ik vind achteraf dat stellingen dichter bij getallen liggen dan ik dacht. Een stelling heeft vele representaties maar de uiteindelijke betekenis is altijd dezelfde, net als elke representatie van een getal tot dezelfde hoeveelheid stippen, strepen, dropjes zal leiden.
Er is meer
In de tweets hadden we het ook over de mogelijkheid boeken en getallen te ordenen en het al dan niet bestaan van getallen.
Daar zal ik het in een latere post een keer over hebben.
KP checkt: Hartslag en de Gulden Snede
In deze blogpost beschreef ik een artikel waarin metingen aan mensenschedels moesten aantonen dat een aantal maten zich volgens de Gulden Snede zouden verhouden. De conclusies waren nogal discutabel maar ook al waren de getallen niet echt dicht bij de Gulden Snede ze leken tenminste te kloppen. In de referenties van het artikel vond ik veel verwijzingen naar andere voorkomens van de Gulden Snede. Twee daarvan heb ik nader bekeken: Golden Ratio is beating in our heart en Does systolic and diastolic blood pressure follow Golden Ratio. Daar kloppen de getallen iets minder goed.
Kloppende getallen
Wat bedoel ik met `kloppende getallen’? Welnu, als je een lengte, zeg A, in twee stukken verdeeld, zeg B en C, dan geldt natuurlijk A=B+C. Als je op jacht bent naar de Gulden Snede neem je de grootste van de twee stukken, zeg C, en dan bekijk je de verhoudingen A/C en C/B. Je hoopt dat die verhoudingen gelijk zijn want dan heb je de Gulden Snede te pakken.
Tussen die twee verhoudingen bestaat een relatie: deel de gelijkheid maar door C dan krijg je A/C=B/C+1, of iets ingewikkelder opgeschreven: A/C=1/(C/B)+1. Als we onze twee verhoudingen even afkorten, A/C=y en C/B=x, dan staat hier y=1/x+1.
Anders gezegd: het punt met coordinaten (C/B,A/C) ligt op de grafiek van y=1/x+1.
In het artikel Mammalian Skull Dimensions and the Golden Ratio worden de volgende gemiddelden van de verhoudingen gerapporteerd: A/C=1.64 ± 0.04) en C/B=1.57 ± 0.10 (de letters zijn anders, maar het gaat om de getallen).
Niet alleen het punt (1.57,1.64) ligt op de grafiek van y=1/x+1 maar ook de punten (1.47,1.68) en (1.67,1.60); deze worden bepaald door de randpunten van de intervallen (1.60,1.68) (voor A/C) en (1.47,1.67) (voor (C/B). Zie het plaatje hieronder.
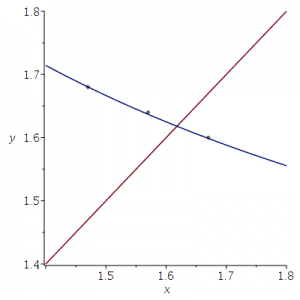
Dit bedoel ik met kloppende getallen: de resultaten horen in ieder geval bij de stituatie waar A=B+C.
Overigens laat ik het aan de lezer om te beoordelen, gezien dit plaatje, in hoeverre deze conclusie gerechtvaardigd is:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Het snijpunt van de twee grafieken (y=1/x+1 en y=x) is het punt (Φ,Φ), en daar ligt (1.57,1.64) toch nog wel ver vandaan.
Hartslag en bloeddruk
In de referenties van het schedelartikel vond ik de artikelen die hierboven genoemd werden.
Hartslag
Om te beginnen: in Golden Ratio is beating in our heart wordt de Gulden Snede ontdekt in verhoudingen van tijdsintervallen in de hartslag. Een mooi plaatje met een uitleg van alle termen staat op de wikipedia-pagina over het QRS-complex:

De drie grootheden waar het hier om gaat zijn: (A) het R-R-interval (tussen twee opeenvolgende R-en), (B) de systole (samentrekfase), en (C) de diastole (ontspanningfase).
De letters komen overeen met onze eerste paragraaf en met de verhoudingen waar het artikel over gaat.
De resultaten zijn
- A=866 ± 73
- B=333 ± 22
- C=536 ± 66
- C/B=1.611
- A/C=1.618
Deze getallen zijn problematisch.
Ten eerste tellen de gemiddelde waarden niet goed op: A=866 en B+C=869. Dat zou wel moeten als alle metingen goed waren dan geldt A=B+C voor elke meting en dan ook voor de gemiddelden.
Ten tweede: als een van de verhoudingen gelijk is aan Φ dan is de andere dat ook, hier is dat niet zo.
Ten derde: als je, net als in het schedelmetingartikel, de verhoudingen van de gemiddelden neemt kom je op andere getallen uit: 866/536=1.61567 en 536/333=1.6096.
Het zou kunnen zijn dat de gerapporteerde verhoudingen gemiddelden zijn van de verhoudingen per meting maar dan hadden de auteurs dat wel even mogen vermelden.
Voorlopig geloof ik niets van de conclusies van het artikel.
Het lijkt er op dat de individuele verhoudingen wel zijn uitgerekend want het artikel bevat nog een niet-ter-zake-doende grafiek waarin de verhouding C/B is uitgezet tegen de hartslag.

Daar is in ieder geval te zien dat de verhouding C/B behoorlijk variabel is.
Bloeddruk
In het artikel Does systolic and diastolic blood pressure follow Golden Ratio gaat het om de bloeddruk. De grootheden zijn nu: (A) de systolische druk (bovendruk), (C) de diastolische druk (onderdruk), en (B) hun verschil; alle in mm Hg.
| A | C | B | A/C=y | C/B=x | |
|---|---|---|---|---|---|
| etmaal | 137 ± 16 | 86 ± 12 | 51 | 1.59 | 1.69 |
| dag | 140 ± 17 | 89 ± 12 | 51 | 1.57 | 1.75 |
| nacht | 131 ± 18 | 80 ± 13 | 51 | 1.64 | 1.62 |
Wat hier opvalt is dat er voor het verschil geen interval is opgegeven; alsof het bij alle metingen precies 51 mm Hg was (dat geloof ik dus niet). De verhoudingen komen hier wel voort uit de gemiddelden behalve de verhouding C/B in de nacht: 80/51=1.56862. Laat die foute 1.62 nou net de verhouding zijn die het dichtst bij de Gulden Snede ligt.
Ik heb de punten vergeleken met de grafiek van y=1/x+1.
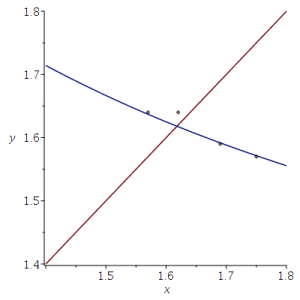
De twee punten rechts horen bij de verhoudingen voor een etmaal en overdag. Het meest linkse punt hoort bij de echte nachtelijke verhoudingen. Het punt dat ruim boven de grafiek ligt hoort bij de gerapporteerde nachtelijke verhoudingen. Ik heb geen idee hoe dat gebeurd kan zijn.
Daar is-tie weer: de Gulden Snede
Niet uit te roeien, die Gulden Snede: via een stukje op Science Alert kwam ik hier: Mammalian Skull Dimensions and the Golden Ratio.
Wat staat er in dat artikel?
Welnu over je schedel loopt een lijn, van het Nasion (N) naar het Inion (I); op die lijn ligt een punt het Bregma (B) geheten. Op honderd mensenschedels zijn de lengten NI, NB en BI gemeten (niet letterlijk, er is gemeten aan hoge-resolutiescans van schedels). Nu geldt, natuurlijk, NB+BI=NI en verder is het deel BI wat groter dan het deel NB.
Op zoek naar de Gulden Snede hebben de auteurs van elke schedel de verhoudingen NI/BI en BI/NB bepaald. Als B de lijn NI inderdaad volgens uiterste en middelste reden verdeelt, dan verwachten we dat NI/BI gelijk is aan BI/NB.
Na middelen en standaard-deviatie nemen komen de auteurs uit op NI/BI = 1.64 ± 0.04 en BI/NB = 1.57 ± 0.10. In de woorden van de auteurs:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Ik weet niet wat de lezer denkt maar in vind dat een krasse uitspraak. De gemiddelden liggen nogal ver uit elkaar. Of je nu vanuit 1.64 of vanuit 1.57 rekent, het verschil is relatief meer dan 4%. Dat lijkt me niet `essentially identical’. Ik denk dat de wens hier toch de vader van de gedachte is geweest.
Overigens zijn de opgegeven waarden wel consistent met de betrekking die tussen de verhoudingen moet gelden: door de gelijkheid NB+BI=NI door BI te delen ontstaat de gelijkheid NI/BI = 1/(BI/NB)+1. Om dit iets overzichtelijker te maken noemen we NI/BI even y en BI/NB even x, de gelijkheid wordt dan y=1+1/x. De punten (1.57,1.64), (1.47,1.68) en (1.67,1.60) liggen op een haar na op de grafiek van deze vergelijking.
Deze betrekking verklaart ook de volgende observatie van de auteurs:
Interestingly, the reciprocal of Φ (1/Φ or 1/1.61803…) is 1 integer less than Φ (0.61803…) and has the same decimal extension as Φ, and the square of Φ (Φ² or 1.61803…2) is 1 integer more than Φ (2.61803…) and also has the same decimal extension.
Uhm, ja, nogal wiedes; de verdeling in uiterste en middelste reden dicteert dat Φ aan de gelijkheid Φ=1+1/Φ moet voldoen, en dus ook aan Φ²=Φ+1. Iedere middelbare-scholier die kwadratische functies heeft gezien kan je dit uitleggen.
Ten slotte
Het artikel beslaat negen kolommen; daarvan zijn er vier gevuld met een verslag van de metingen; er is ook aan zes andere zoogdiersoorten gemeten en het lijkt er op dat bij toenemende `complexiteit’ van de soort de verhouding NI/BI daalt en BI/BN dus stijgt. De (speculatieve) uitleg is dat gaande de evolutie de schedel op deze manier bij bepaalde kwabben is gaan passen.
Als de auteurs zich nu maar bij deze conclusie hadden gehouden dan was er weing mis geweest met dit artikel. De overige vijf kolommen zijn echter gevuld met niet ter zake doende beschrijvingen van de Gulden Snede, de relatie met de rij van Fibonacci, en het vermeende optreden van dit getal bij allerlei fysiologische en morphologische verschijnselen.
Allerlei al lang onderuit gehaalde mythes over de Gulden Snede worden weer van stal gehaald en als belangwekkende feiten gepresenteerd.
In het fraaie boek De Ontstelling van Pythagoras heeft Albert van der Schoot vrijwel niets heel gelaten van alle flauwekul die over de Gulden Snede verteld wordt. De recensie in NRC noemt er al een paar. En lees ook het artikel Het is niet alles goud wat er snijdt van Van der Schoot in het Nieuw Archief voor Wiskunde.
Ook deze column van Keith Devlin is het lezen meer dan waard.

Recent Comments