Posted in August 2018
En tau rund jorden, II
Dette er andre delen av en oversettelse av en artikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger). Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen? Kan vi uttrykke høyden i lengden vi spleiset inn?
I går vi så at når vi tar en tau som er en meter langre enn jordens omtrekk og drar tauen strammt ved Nordpolen så skal det høyeste punktet være på 121 meter og lit mer. I dag skal vi lage en enkel formel med radiusen og ekstra lengden i som gir en god approksimasjon av høyden.
En effektiv approksimasjon
Her er tegningen fra i går igjen
Fra Pythagoras sin læresetning lærte vi at
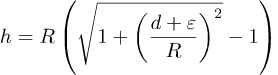
Fra bildet ser vi også at
![]()
Dette kan kombineres til denne ligningen
![]()
Nå har vi et uttrykk for h som bruker R og α men vi trenger et som bruker ε. Dette må gjøres implisitt fordi α er en løsning av
![]()
og der er ingen `pen’ (eller stygg) formel for løsningene.
Som vi så i går er vinkelen α veldi liten (0.006176 radianer). Nå er det slik at α+α3/3 er en veldi bra approksimasjon av tanα. Hvis vi setter dette uttrykket i ligningen så får vi
![]()
Også tanα er veldi liten.
Og for x nær 0 har vi √(1+x)≈1+½x; nå kan vi forenkle formelen for h til en approksimasjon
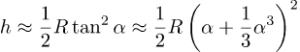
Neste steg er å skrive ut kvadraten
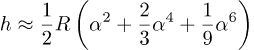
Når vi setter i tallene så får vi Rα2=242.8 m, Rα4=0.009 m og Rα6=3.5×10-7 m. Vi derfor kan trygt kaste fjerde og sjette potensene og så får vi denne approksimasjonen for h:
![]()
Lit lengre siden fant vi at
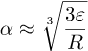
Vi setter det inn i approksimasjonen og får
![]()
Nå bruker vi verdien av R og får til slutt
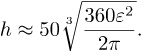
Det flotte med denne formelen er at den gir nesten samme svaret som i går: setter vi inn ε=0.5 så får vi h≈121.4 m igjen.
Oppgav
Sett inn ε=0.005 in formelen vår. Hvor mye forskjeller resultatet fra verdien av h som vi fikk i går?
Exercise
Undersøk hvor bra approksimasjonen √(1+x)≈1+½x er. For eksempel, sammenlign (1+½x)2 med 1+x; for hvilken x er forskjellen liten nok til å bli kastet? Er du enig i hvordan approksimasjonen brukes her?
Bemerkning
Vi kan isolere ε i formelen:
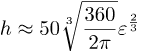
dette gir viktig kvalitativ informasjon: h er omtrent lik en konstant ganger ε2/3.
Hvis du er kjent med Taylorpolynomer kann det være gøy å finne ut hvor stor feilen er (hvilken potens av ε) i denne approksimasjonen.
En tau rund jorden, I
Dette er første delen av en oversettelse av en art ikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger).
Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.
Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen?
Fast alle har hørt om følgende oppgaven. Vi tar en tau og strekker den rund jorden, langs polene, slik at den sitter tett. På Nordpolen spleiser vi inn en ekstra meter tau. Så drar vi, og mange folk rund jorden, tauen opp slik at den er overalt like høyt over jordoverflaten; den blir en sirkel igjen. Hvor høyt kommer den til å bli? Kan en mus komme seg under tauen?
Svaret, tauen skal være overalt 16 centimeter høyt, blir en overraskelse for mange folk. inntil du utfører beregningen. Vi begynner med en tau som er 2πR lang, der R er jordens radius. Oppgaven er å bestemme radiusen til sirkelen som er en meter lengre. Det vil si: bestem R’ slik at 2πR’=2πR+1. Men det er lett å gjøre: divider med 2π, så får vi R’=R+1/(2π)≈R+0.159.
Beregninger viser at verdien av R er ikke viktig: hvis du forlenger en sirkel med en meter så forlenger du radiusen med nesten 16 centimeter.
Vi henger jorden på en spiker
Men hva om vi drar opp tauen bare på Nordpolen til den er helt stramm igjen? Som om vi skule bruke tauen til å henge jorden på en spiker. Hvor høyt kommer spikeren til å bli over Nordpolen? Kan en isbjørn komme seg under tauen?
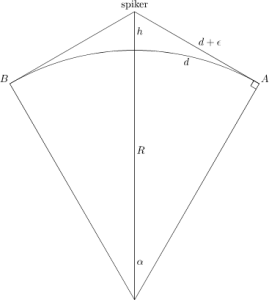
Her er en tegning som viser hva vi prøver å gjøre.

Det er lit enklere med bokstaver: R er jordens radius, ε er halvparten av tauen vi spleiset inn (en halv meter altså) og h er svaret på spørsmålet.
Buen d viser distansen fra Nordpolen til begge punktene der tauen sist berører jorden.
Vi har en rett vinkel i A (og B) fordi linjen fra A til spikeren er en
tangent til sirkelen. Nå kan vi finne en formel for h.
Vi begynner med Pythagoras sin læresetning:
![]()
og så h+R=±√(R2+(d+ε)2), eller
![]()
Dersom h er positiv må vi ta plussen, og
![]()
Vi tar R utenfor parentesen og får
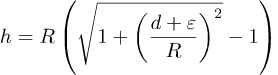
Det vi ikke vet her er verdien til d. Vi bruker radianer, og derfor d=αR eller α=d/R fordi, som vi skal se, det er enklere å lage en ligning for α.
Fra bildet ser vi hva tangensen til vinkelen α er:
![]()
og derfor
![]()
eller
![]()
Så, vår α er en løsning på siste ligningen.
Nå trenger vi noen tall. Jordens omkrets er, per definisjon, 40.000 km
(se illustrasjonen her). Derfor R=40.000.000/(2π) m og, selffølgelig, ε=½ m. Det betyr at vi må løse
![]()
Det finnes ingen enkelt formel for løsningen; det beste vi gjøre er å løse ligningen numerisk. De fleste grafiske kalkulatorene kan gjøre det for deg og jeg fikk denne løsningen: alpha;≈0.006176=6.176×10-3 og det betyr at d≈247.040 km. Det er interessant å vite hvor langt fra Nordpolen tauen forlater jorden men vi trenger ikke d i beregningene våre: vi setter α for d/R in formelen for h:
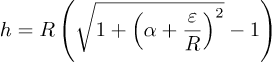
Når vi taster alle tallene in kalkulatoren får vi h≈121.4 m.
Oppgave
Gjør alt igjen men nå spleiser du inn bare en centimeter tau. Hvis tauen er lett nok kan du dra den stramm uten hjelp?
Selv om vi ikke har en eksakt formel for h som involverer ε og R kan vi noe om relasjonen mellom de tre størrelsene. Jeg skal skrive noe om det senere, in andere delen av denne historien.
Hon hade blivit kissnödig
Sometimes I read a book for an odd reason. In this blog a reader expressed surprise that `pee’ was being used as a noun to indicate the act of peeing, as in “She needed a pee”. This piqued my interest not because of the issue of noun versus verb but because I wanted to know what was in the Swedish original, `Solstorm’ by Åsa Larsson.
The original sentence was “Hon hade blivit kissnödig”. I found it difficult to come up with a faithful translation that is as compact as the original. Both “She needed to pee” and “She needed a pee” come close but they do not convey the exact meaning. A too-literal translation runs as follows: “She had become piss-necessary”; the `necessary’ chafes here. The term `piss-pressed’ might be better, but I could not come up with one word that describes the state of having the need to micturate.
The Swedish `att kissa’ means `to piss’ and it is an obvious candidate for a false friend between that language and English. It turns out that Google Translate has problems with the sentence too. When I had it translate “Hon hade blivit kissnödig” I got
- English: She had become kissed
- Dutch: Ze was gekust
- Norwegian: Hun ble blitt kysset
Be careful what you ask for in Sweden.

Recent Comments