Posted in February 2018
KP checkt: 200 liter inkt
Op twitter toonde Dap Hartmann zich een aanhanger van regel 17 uit The Elements of Style: Omit needless words (er zijn twee regels 17, dit is de eerste). Dat zou hem bij het nakijken wel 200 liter (rode?) inkt per jaar besparen.
Navraag leerde dat Dap met een vulpen nakijkt. Een snelle zoektocht leerde dat vulpeninkt in potjes van, onder meer, 60 en 80 ml wordt verkocht. Nu rekent 80 ml iets makkelijker: er gaan 12.5 van die potjes in een liter, en dus 2500 potjes in 200 liter.
Als Dap 50 weken per jaar van maandag tot en met vrijdag zit na te kijken (welk een plichtsbetrachting) dan komen die 200 liter neer op 10 potjes inkt per dag.
Ik denk dat Dap van de stijlfiguur `overdrijving’ gebruik heeft gemaakt.
Fruitmanden samenstellen
Op Facebook stond in de groep Wiskundelessen de volgende vraag (verkort weergegeven): “Hoeveel fruitmanden met zes stuks fruit kun je samenstellen uit vier kiwis, vijf bananen, zes peren, en zeven appels?” De vraagsteller wist dat het antwoord 79 moest zijn maar zag geen manier om daar aan te komen.
Een reageerder vond 79 wel erg weinig want het aantal manieren om 6 dingen uit 22 te kiezen, zonder op de volgorde te letten, is gelijk aan de binomiaalcoëfficiënt 22 boven 6 en die is gelijk aan 74613.
Dat antwoord zou kloppen als de vruchten er wel erg verschillend uit zouden zien. De vraagstelling vermeldt dat niet en het antwoord 79 suggereert dat de vruchten van dezelfde soort ononderscheidbaar zijn.
Hoe pak je zoiets aan? Elke fruitmand is eigenlijk een woord van zes letters, gekozen uit {k,b,p,a}, en gesorteerd: eerst de k’s, dan de b’s, de p’s, en aan het eind de a’s . Bijvoorbeeld kkbbpa, aaaaaa, ppppp, … Die woorden kun je lezen als producten: k2b2pa, a6, p6, … Het komt er dus op neer al dat soort producten te tellen. Hoe doe je dat systematisch, zonder een product te missen?
Dat gaat het best met wat eenvoudige algebra, werk het volgende product uit:
(1+k+k2+k3+k4)(1+b+b2+b3+b4+b5)(1+p+p2+p3+p4+p5+p6)(1+a+a2+a3+a4+a5+a6+a7)
Je krijgt dan alle mogelijke gesorteerde woorden met ten hoogste vier k’s, vijf b’s, zes p’s en zeven a’s.
Nu nog even de woorden van zes letters opzij zetten en tellen: klaar.
Dat kan nog iets sneller: maak van elke letter een x. Elk woord van zes letters wordt dan x6 en dat maakt het uitwerken van het product wat makkelijker.
(1+x+x2+x3+x4)(1+x+x2+x3+x4+x5)(1+x+x2+x3+x4+x5+x6)(1+x+x2+x3+x4+x5+x6+x7)
Met (be)hulp van Maple is het resultaat snel gevonden:
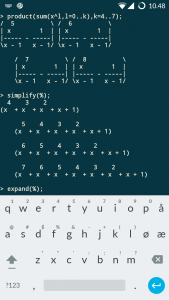
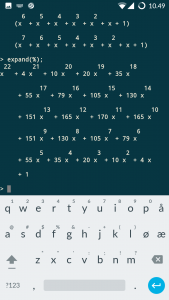
Inderdaad: 79 fruitmanden met zes vruchten. We kunnen nu ook aflezen hoeveel fruitmanden met andere aantallen vruchten gemaakt kunnen worden.
In het februarinummer uit 2016 van Pythagoras staat nog meer over deze manier van combinaties tellen.

Recent Comments