Posts in category Uncategorized
Eindexamen Wiskunde-B, vwo, 2022-06-17
Ik heb het examen gemaakt en van commentaar voorzien.
De opgaven zijn te vinden op examenblad.nl. Hier zijn mijn uitwerkingen en commentaar. Ik vond het iets minder opwindend dan het eerste examen. Het grootste gedeelte van de tekst bij de-som-met-een-toepassing had niets met de opgave zelf te maken.
Eindexamen Wiskunde-B, vwo, 2022-05-20
Ik heb het eindexamen gemaakt en van commentaar voorzien.
De opgaven zijn de vinden op examenblad.nl. Hier zijn mijn uitwerkingen en commentaar. Ik vond het examen te doen. Van de twee verhalen-bij-de-opgaven vond ik die van het tekenen van letters niet zo sterk, de opgaven over de lavabommen sneden iets meer hout.
Eindexamen Wiskunde-B, havo, 2022-05-13
Ik heb het examen maar weer eens gemaakt en van commentaar voorzien.
De opgaven zijn te vinden op examenblad.nl. En hier zijn mijn uitwerkingen en commentaar. Het examen had een mix van `echte’ sommen en sommen met verhaaltjes. De sommen met verhaaltjes hadden uiteindelijk niet altijd echt veel met het onderwerp te maken.
De tafel van oneindig III: twee keer oneindig
We gaan zien dat de tafel van oneindig eigenlijk heel eenvoudig is: twee keer oneindig is oneindig, drie keer oneindig is oneindig, vier keer oneindig is oneindig, … Maar het is niet helemaal eenvoudig in te zien dat die tafel zo eenvoudig is …
Laten we beginnen met twee keer oneindig. We hebben twee zakken met oneindig veel M+M’s: een zak met blauwe en een zak met rode. Die M+M’s leggen we neer en wel zo dat we duidelijk twee keer oneindig zien:
Ik heb de rechthoek maar gekanteld, anders was het plaatje wel erg hoog en dun geworden. Nu willen we zien dat we evenveel M+M’s hebben als in één zak met oneindig veel oranje M+M’s. Dat doen we met de hagelslagmethode: de blauuwe en rode M+M’s op een rij leggen naast de oranje M+M’s op zo’n manier dat elke blauwe/rode bij één oranje M+M hoort, en elke oranje M+M naast één blauwe of rode ligt.
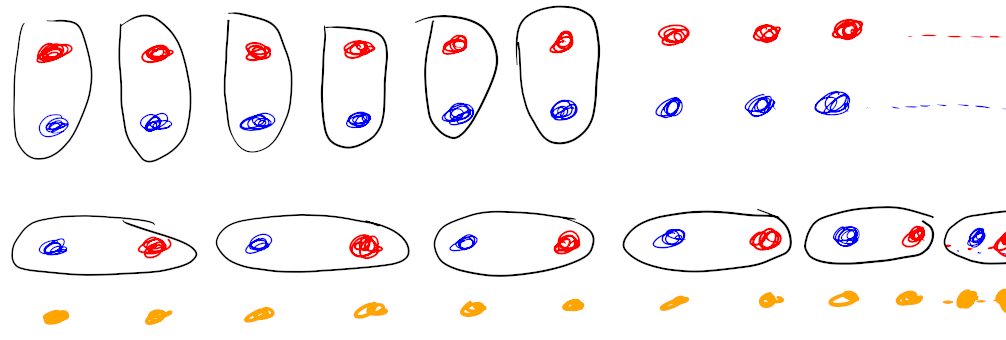
We leggen eerst de oranje M+M’s op een rij. Daarna nemen we telkens een de meest linkse blauwe en een rode M+M’s en leggen die achterelkaar, blauw eerst en dan rood, naast de eerste twee oranje M+M’s die nog geen blauwe of rode buur hebben. Omdat de M+M’s netjes op rijtjes liggen komen ze allemaal aan de beurt: elke blauwe en elke rode krijgt één oranje partner, en elke oranje krijgt één blauwe of rode partner.
In twee zakken met oneindig veel M+M’s zitten er net zoveel als in één zak. Dat klinkt gek, maar in de wereld van oneindig werken sommige dingen nou net anders dan je zou verwachten.
Laat nu zelf maar eens zien dat drie keer oneindig gelijk is aan oneindig; volg de methode voor 3×5 maar, met blauwe, rode, en groene M+M’s. En als dat lukt kun je ook wel zien waarom de tafel van oneindig iedere keer hetzelfde antwoord oplevert: vier keer oneindig is oneindig, vijf keer oneindig is oneindig, …
En oneindig keer oneindig? Oneindig veel zakken met elk oneindig veel M+M’s? Daar zitten er net zoveel in als in één zak met oneindig veel M+M’s. Maar dat zien we volgende keer wel.
De tafel van oneindig II: vermenigvuldigen
De tafel van oneindig heeft te maken met vermenigvuldigen. We eerst even kijken hoe dat ook al weer werkt.
We doen niet al te moeilijk en bekijken 2×3. Dat product kun je tekenen: een rechthoek die 2 breed is en 3 hoog.
Als we de stippen tellen zien we dat 2×3=6. Je kunt die stippen dus op een rijtje leggen:
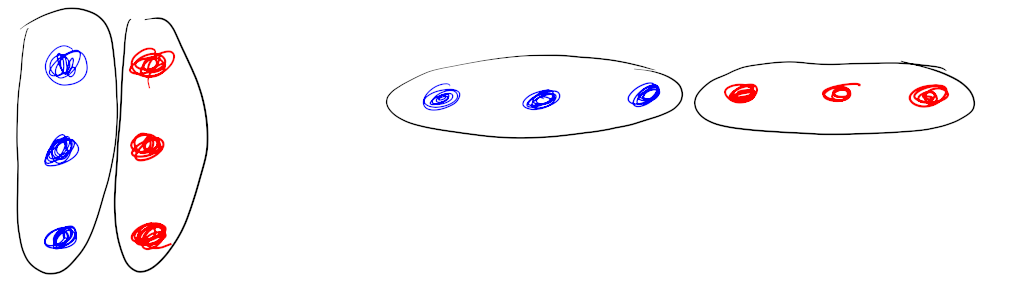
Dat kan op verschillende manieren; ook op deze manier:
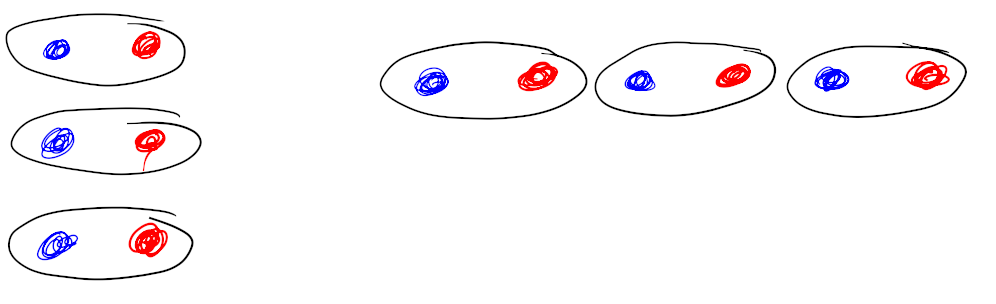
In beide gevallen krijg je een mooi rijtje van zes stippen.
Je kun dit naspelen met chocoladehagel, of M+M’s: als je 3×5 wilt bepalen maak je een rechthoek met vijf blauwe in de eerste kolom, dan vijf rode, en dan nog vijf groene. Die kun je dan mooi op één lijn leggen naast vijftien oranje M+M’s
Met dit soort plaatjes gaan we volgende keer de tafel van oneindig maken.
De tafel van oneindig I: meer, minder, of evenveel?
Op twitter werd naar de tafel van oneindig gevraagd. Die tafel is een beetje saai, er komt altijd oneindig uit. Voor we gaan zien waarom dat zo is moeten we eerst kijken hoe wiskundigen nagaan of in twee verzamelingen evenveel dingen zitten. Dat gaat niet altijd door te tellen want dat duurt soms wat lang, en als je onderweg gestoord wordt raak je misschien de tel kwijt, en moet je weer opnieuw beginnen.
Ik heb hier twee lepels chocoladehagelkorrels.
In welke lepel heb ik meer korrels? Of zitten er evenveel korrels in de lepels?
Hoe doe je dat zonder tellen? We leggen de korrels op een rijtje en vergelijken de rijtjes.
Die rijtjes maken we door telkens van elke hoop een korrel te nemen en die aan het eind van het rijtje te leggen.
Ik ben begonnen maar de korreltjes rolden telkens weg, dus ik heb het iets anders aangepakt: ik heb telkens van elk hoopje één korrel gepakt en die meteen opgegeten (ik heb het de rijtjes meteen in mijn maag gestopt) .
Aan het eind waren er rechts nog een paar korrels over, dus in de rechterlepel zaten meer korrels dan in de linker.
Je kunt dit idee voor andere gewichtige vragen gebruiken: zitten er evenveel paaseitjes in de zakjes uit de winkel? Zijn er evenveel stoelen als mensen? Zo ja, dan is de stoelendans niet echt spannend.
Dit is hoe we in de wiskunde verzamelingen vergelijken: zet ze naast elkaar op een rijtje en kijk of ze even lang worden. Dat idee gaan we volgende keer gebruiken om de tafel van oneindig op te stellen.
Perforaties en definities
Op Facebook, in de groep Leraar Wiskunde, kwam een vraag langs die een mooi excuus oplevert voor een wat algemenere beschouwing over definities.
Perforaties
De vraag ging over perforaties in grafieken van functies. Een perforatie is een gat in de grafiek dat gedicht kan worden op zo’n manier dat de functie continu wordt in dat punt. Dit was de informele definitie.
De formele definitie werd in de vraag uit een leerboek geciteerd: de grafiek van f heeft een perforatie in (a,b) als f(a) niet bestaat en als de limiet van f(x) voor x nadert tot a gelijk is aan b. Verder kwam een voorbeeld uit het boek ter sprake waarin duidelijk aan deze definitie werd voldaan. Einde verhaal zou je zeggen. Ware het niet dat de vraagsteller vond dat er `gevoelsmatig’ meer aan de hand zou moeten zijn. Ik heb het voorbeeld nagetekend.
De functie is links en rechts van 2 door verschillende formules gegeven en f(2) is expliciet niet gedefinieerd. Aan de eerste eis is voldaan: f(2) bestaat niet. Verder zijn linker- en rechterlimiet snel bepaald, ze zijn gelijk aan 2. Daar is de tweede eis: de limiet is gelijk aan 2. We hebben een perforatie in (2,2). De vraagsteller vond (`gevoelsmatig’) dat eigenlijk de linker- en rechterlimieten van de afgeleide ook aan elkaar gelijk zouden moeten zijn.
Definities
De discussie onder de vraag ging eigenlijk meer over wat een perforatie zou moeten zijn in plaats van wat het eigenlijk is. Wat aan het geciteerde boek valt te prijzen is dat er een definitie gegeven is. En die definitie is een minimale exacte beschrijving van: “er zijn een gat in de grafiek dat bij opvulling de functie in dat punt continu maakt”. De eis dat f(a) niet bestaat is de vertaling van “er is een gat” en de eis dat de limiet bestaat vertaalt “bij opvulling wordt de functie continu in dat punt”.
In een paar andere bronnen vond ik niet meer dan een definitie door voorbeeld: “als wat hier gebeurt elders ook gebeurt spreken we van een perforatie”.
Het voordeel van de definitie uit het boek is dat deze kort en krachtig is en daardoor ook zonder omhaal te verifiëren. In de discussie op facebook kwamen wel bezwaren naar voren maar die waren denk ik ingegeven door non-definities als die uit de andere bronnen. In de voorbeelden was vaak meer aan de hand: de functies was bijvoorbeeld een rationale functie waarin de kandidaat-perforaties onder de nulpunten van de noemer gezocht werden en door gemenschappelijke factoren in teller en noemer geïdentificeerd konden worden. En `eigenlijk’ zouden alle perforaties er zo uit moeten zien.
Maar de kracht van de meeste wiskundige definities is juist het kernachtige ervan. Bolzano had een definitie van continuïteit die heel dicht bij de huidige kwam en die is met ε en δ en al afkomstig van Weierstrass. Die definitie bleek echt het wezen van de continuïteit te vangen: hij geeft ons de Tussenwaardestelling (van Bolzano) en de het bestaan van extremen op gesloten intervallen (Weierstrass).
De definitie laat ook schijnbare uitwassen toe met als de mooiste voorbeelden (voor mij) de nergens differentieerbare functies van Weierstrass en Peano’s vlakvullende kromme. Hermite moest er niets van hebben, zoals hij aan Stieltjes schreef: “Je me détourne avec effroi et horreur de cette plaie lamentable des fonctions continues qui n’ont point de dérivées …”.
De moraal: de taak van een definitie is de kern van de zaak samen te vatten. Dat doet de definitie van perforatie prima, en met niet meer dan echt nodig is.
Alternatieve functies?
Een vraag op de Wisfaq:
De exponentiële functie exp(ax), waarbij a een constante is, is voor alle x-waarden positief. Dat geldt voor zowel negatieve als voor postieve x-waarden. Als deze functie echter voorkomt in andere functies wordt het vinden van een uitdrukking bij integreren dikwijls onmogelijk.
Bestaat er een alternatief voor deze functie, waarbij als de functie voorkomt in een andere functie integreren wel makkelijk gaat? In het alternatief moet dus ook gelden, dat de functie voor alle x-waarden positief is en ook gedefinieerd is voor alle x-waarden.
Ik vind deze vraag tegelijkertijd aardig en onzinnig.
Aardig
Hoezo “aardig”? Ik begrijp de frustratie als een uitdrukking weer eens niet in gesloten vorm te primitiveren blijkt en ik kan me voorstellen dat iemand zich afvraagt of we daar niets aan kunnen doen. Maar, helaas, die frustratie gaat voorbij aan de werkelijkheid en daarom …
Onzinnig
Het woord “onzinnig” klinkt wat scherp maar ik kon niet iets beters verzinnen. Primitiveren in gesloten vorm heeft zijn charmes en zijn nut; het is altijd leuk iets in een niet al te lelijke formule te vangen en die expliciete primitieven kunnen tot verder inzicht leiden.
Echter, en dat komt misschien als een verassing, eigenlijk is dat primitiveren in gesloten vorm min of meer een illusie.
Iemand die alleen kan optellen, aftrekken, vermenigvuldigen, en delen ken alleen de zogeheten rationale functies: quotiënten van polynomen. Die persoon zal niet in staat zijn de functie 1/x te primitiveren. Maar die primitieve is belangrijk bij het bepalen van oppervlakten van gebieden begrensd door hyperbolen. De oplossing: geef die primitieve een naam en probeer zoveel mogelijk eigenschappen van die functie te vinden om ermee te kunnen werken. Die functie heet nu de natuurlijke logaritme en is onderhand een `bekende’ functie geworden. Net zoals de inverse van die natuurlijke logaritme en dat is de exponentiële functie. Die functies zijn zo grondig bestudeerd dat ze net als optellen, aftrekken, vermenigvuldigen, en delen tot ons standaardgereedschap zijn gaan behoren, net als onderhand ook allerhande wortel- en de goniometrische functies. Bedenk hierbij dat zelfs √x een impliciet bepaalde functie is: de inverse van de kwadraatfunctie.
In dit verband zou je naar analogie van de wisfaqvraag kunnen verzuchten: “Kunnen we dat delen niet door wat anders vervangen want we kunnen veel breuken niet primitiveren.”
In de mathematische fysica, kansrekening, en vele andere toepassingsgebieden van de Analyse komen die vervelende niet-te-primitiveren functies heel vaak voor en men heeft daar gedaan wat dus eerder met de logaritme en exponentiële functie is gebeurd: de primitieven hebben namen gekregen.
Bijvoorbeeld exp(-x2), bekend van de normale kansverdeling; de primitieve heeft een naam gekregen: de Error function. En onder de gebruikers is die Errorfunctie net zo vertrouwd als de `elementaire’ functies van de Analyse. Er zijn nog veel meer van dit soort functies benoemd, zie bijvoorbeeld de Wikipediapagina over Special Functions.
Daarnaast, en dat is eigenlijk de hoofdreden voor het predicaat “onzinnig”, de exponentiële functies zijn niet voor niets zo alomtegenwoordig; zo ongeveer elke poging processen in de echte wereld te beschrijven leidt tot deze functies of functies waar deze in verstopt zit. Je kunt hem wel weg willen wensen maar de werkelijkheid is te weerbarstig.
Wat zou het nut van die alternatieve functies zijn?
Hoeveel reële getallen?
Een paar maanden geleden stond er een artikel in Quanta magazine over het aantal reële getallen, een vraag die verzameltheoreten al bijna 150 jaar bezig houdt.
Het begin van het artikel beschrijft in de ietwat hijgerige stijl van Quanta de vermeende implicaties van een recent resultaat van David Asperó en Ralf Schindler: een implicatie tussen twee niet-triviale verzameltheoretische principes.
Die implicaties betreffen Cantor’s ContinuumHypothese. De oorspronkelijke formulering had te maken met het indelen van de oneindige deelverzamelingen van de reële rechte R in klassen door middel van bijecties (een-op-eencorrespondenties). Cantor dacht/vermoedde dat er voor een oneindige deelverzameling, X, van R maar twee mogelijkheden ware: in bijectie met R zelf of in bijectie met de verzameling N der natuurlijke getallen.
Later kwam er een nieuwe versie van dat vermoeden. Cantor had namelijk een meetlat van kardinaalgetallen ontwikkeld om aan oneindige verzamelingen ook een “aantal elementen” toe te kunnen kennen. Die getallen werden genoteerd als ℵα, waarbij α een andere meetlat doorloopt. Cantor’s vermoeden kwam neer op de bewering dat zijn toekenning van “aantal elementen” voor R het resultaat ℵ1 zou geven. Wat we nu weten is dat de huidige axioma’s van de verzamelingenleer niet sterk genoeg zijn om te bewijzen dat het “aantal elementen” van R inderdaad gelijk is aan ℵ1 (het kleinst mogelijke), en ook niet sterk genoeg om te bewijzen dat dat niet zo is.
Door de jaren heen hebben verzameltheoreten geprobeerd nieuwe axioma’s te formuleren die “natuurlijk” zijn en die een definitief antwoord geven op de vraag naar het “aantal elementen” van R. Het resultaat van Asperó en Schindler verbindt twee van dergelijke axioma’s. Het ene heet Martin’s Maximum++ en het andere gaat onder de weinig informatieve naam (*). Beide impliceren dat het “aantal elementen” van R gelijk is aan ℵ2. Dat is n kardinaalgetal hoger dan Cantor hoopte en zegt dat er voor de oneindige deelverzamelingen van R nog een derde mogelijkheid is naast de twee die hierboven genoemd zijn.
Wat Asperó en Schindler hebben laten zien is dat (*) een gevolg is van Martin’s Maximum++. Wie het artikel leest zal zien dat de formuleringen van de twee principes en het bewijs van de implicatie verre van eenvoudig zijn. Dat bewijs mag met een gerust hart een mijlpaal genoemd worden.
Maar brengt het ons dichter bij de oplossing van Cantor’s probleem? Dat is nog maar de vraag, zoals gezegd: de principes zijn niet eenvoudig en hun consistentie met de gebruikelijke axioma’s vergt nogal wat machinerie. Daar hebben we het nog niet over gehad: het is mooi dat die principes een oplossing van Cantor’s probleem opleveren maar dat helpt niet als hun negaties uit de gebruikelijke axioma’s af te leiden zouden zijn. Dat is gelukkig niet zo maar de moeite die het kost dat vast te stellen laat ze wat minder natuurlijk klinken.
Aan het eind van het stuk in Quanta wordt een even natuurlijk (of even onnatuurlijk zo u wilt) principe besproken dat Cantor’s probleem nu juist oplost zoals Cantor dat wilde.
Wat is nu de conclusie? Er is in het bouwwerk van implicaties tussen allerlei verzameltheoretische principes een belangrijke pijl toegevoegd. Maar die nieuwe pijl brengt ons (in tegenstelling tot de titel van het artikel) niet echt dichterbij een oplossing van Cantor’s probleem. De nieuwe pijl maakt de principes die hij verbindt niet automatisch meer natuurlijk dan andere potentiële axioma’s.
Eindexamen wiskunde B vwo 2021-07-07
Eergisteren was de derde gelegenheid voor wiskunde B (vwo). De opgaven staan op examenblad.nl. Ik heb de opgaven gemaakt en eigenlijk weinig commentaar, ze leken mij goed te doen. Zelfs de `contextopgave’ was redelijk, zonder al te veel tekst.
Recent Comments