Lariekoek? I
Dit is de vierde in een korte serie blogposts naar aanleiding van een discussie op twitter over dit stuk op Neerlandistiek.nl van Marc van Oostendorp dat zelf weer een reactie op dit artikel van Paul Postal was. In de eerste post kwalificeerde ik een opmerking uit het stuk van Postal als lariekoek. Daar gaat deze post over.
De opmerking van Postal betreft de grootte van de `collectie’ van alle boeken in een taal. Die collectie is niet alleen oneindig groot, niet alleen overaftelbaar, maar zelfs groter dan elke denkbare verzameling. Voor (een idee van) het bewijs van deze bewering verwijst Postal naar het artikel Sets and Sentences en een boek, The Vastness of Natural Languages, beide geschreven door hemzelf en D. Terrence Langendoen.
Ik heb wat met verzamelingen en wilde daarom wel eens zien waarom de collectie boeken in een Natuurlijke Taal zo groot moest zijn. Het boek heb ik niet te pakken kunnen krijgen maar deze recensie beweert dat de kern van de inhoud al in het artikel staat. laten we dat artikel dan maar eens bekijken.
Het artikel bestaat uit drie delen: een korte inleiding, een deel waarin “naar analogie met Cantors’s resultaten” wordt beargumenteerd dat de zinnen in een natuurlijke taal geen verzameling vormen, en een deel met conclusies.
Dat tweede deel begint met wat definities die het beschrijven van constructies van nieuwe `zinnen’ uit oude mogelijk moeten maken. Het hoofdingrediënt is dat van een conjunct, dat is een eenheid die bestaat uit een connectief en een deelconjuct. Die conjuncties kunnen in/tot `co-ordinate compound constituents’ samengevoegd worden. Zo’n co-ordinate compound moet wel echt `compound’ zijn en dus uit ten minste twee conjuncten gevormd worden.
Vervolgens spreken de schrijvers af hoe uit een verzameling U van constituents een co-ordinate compound constituent T gemaakt kan worden; of beter: hoe we kunnen zien dat T uit U gemaakt is. Elke conjuct in T heeft een element van U als deelconjunct, elk element van U is deelconjunct van precies één conjuct van T, en de conjuncten in T zijn geordend (daarover later meer).
In dit geval is T een `co-ordinate projection‘ van U, en U is de `projection set van T. Let op het gebruik van `een’ en `de’ in de vorige zin.
Ik kan begrijpen dat dit allemaal nogal abstract overkomt en ik moest het zelf een paar keer lezen voor ik dacht door te hebben wat er aan de hand is. Achter al die termen zitten plaatjes als het onderstaande verscholen:
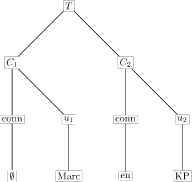
De verzameling U bestaat uit de constituents `Marc’ en `KP’; uit elk element van U kunnen we een conjunct maken door er een connectief aan vast te plakken. Dat connectief kan leeg zijn, zoals bij `Marc’ omdat, bijvoorbeeld, je aan het begin van een zin geen voegwoord gebruikt en toch iets nodig hebt om je conjuct te markeren. Daar nemen we dan ∅ maar voor. In de woorden van Langendoen en Postal: C1 en C2 zijn de dochters van T, die zusters zijn elk een conjuct, bestaande uit een connectief en een deelconjuct.
De hoofdaanname, of het hoofdaxioma, is nu dat elke verzameling constituents tot een co-ordinate compound constituent gevormd kan worden. De (co-ordinate compound) constituents waar we het verder over zullen hebben zijn gewoon zinnen, en daarom zal ik ze verder ook maar zo noemen.
Om te beginnen maken we oneindig veel zinnen:
- De reële rechte is overaftelbaar
- Ik weet dat de reële rechte overaftelbaar is
- Ik weet dat ik weet dat de reële rechte overaftelbaar is
- Ik weet dat ik weet dat ik weet dat de reële rechte overaftelbaar is
- …
Niet erg opwindende zinnen maar daar gaat het niet om: er is een duidelijke procedure die voor elk natuurlijk getal n een zin Z(n) construeert. Dit is een voorbeeld van een recursieve definitie: als we een beginobject beschrijven en een recept aangeven om elk volgende object te maken dan beschouwen we de constructie als voltooid.
Voor elke deelverzameling U van deze verzameling {Z(n):n∈N} van zinnen bestaat er dus een zin waarvan de deelconjucten precies de zinnen uit U zijn. Dat geeft ons dan overaftelbaar veel zinnen.
Daarmee is het hek van de dam: we kunnen blijven doorgaan en elke deelverzameling van de nieuwe verzameling zinnen weer samensmeden tot een nieuwe zin. En weer, en weer, en weer, …
De conclusie van Langendoen en Postal is nu dat alle zinnen die we zo kunnen maken geen verzameling vormen. Hier komt de analogie met Cantor’s resultaten om de hoek kijken. Cantor bewees namelijk dat elke verzameling strikt meer deelverzamelingen heeft dan elementen. Als je dit toepast op `de verzameling van alle verzamelingen’ kom je in de knoop: de elementen van die `verzameling’ zijn precies zijn deelverzamelingen, maar dat kan niet omdat er meer deelverzamelingen dan elementen zijn. De entiteit `de verzameling van alle verzamelingen’ bestaat dus niet.
Dezelfde redenering is nu van toepassing op `de verzameling van alle zinnen in een natuurlijke taal’: elke deelverzameling bepaalt een zin en verschillende deelverzamelingen bepalen verschillende zinnen en dat druist in tegen de conclusie van Cantor: altijd strikt meer deelverzamelingen dan elementen.
Waarom Lariekoek?
Waarom denk ik dat dit lariekoek is? Dat heeft vooral te maken met de manier waarop Langendoen en Postal hun `bewijs’ presenteren. Daar is wiskundig veel op af te dingen. Maar deze post is al behoorlijk lang en ik bewaar mijn wiskundige opmerkingen, bijvoorbeeld over de bovengenoemde ordeningen daarom maar voor deel twee.





Recent Comments