KP checkt: Hartslag en de Gulden Snede
In deze blogpost beschreef ik een artikel waarin metingen aan mensenschedels moesten aantonen dat een aantal maten zich volgens de Gulden Snede zouden verhouden. De conclusies waren nogal discutabel maar ook al waren de getallen niet echt dicht bij de Gulden Snede ze leken tenminste te kloppen. In de referenties van het artikel vond ik veel verwijzingen naar andere voorkomens van de Gulden Snede. Twee daarvan heb ik nader bekeken: Golden Ratio is beating in our heart en Does systolic and diastolic blood pressure follow Golden Ratio. Daar kloppen de getallen iets minder goed.
Kloppende getallen
Wat bedoel ik met `kloppende getallen’? Welnu, als je een lengte, zeg A, in twee stukken verdeeld, zeg B en C, dan geldt natuurlijk A=B+C. Als je op jacht bent naar de Gulden Snede neem je de grootste van de twee stukken, zeg C, en dan bekijk je de verhoudingen A/C en C/B. Je hoopt dat die verhoudingen gelijk zijn want dan heb je de Gulden Snede te pakken.
Tussen die twee verhoudingen bestaat een relatie: deel de gelijkheid maar door C dan krijg je A/C=B/C+1, of iets ingewikkelder opgeschreven: A/C=1/(C/B)+1. Als we onze twee verhoudingen even afkorten, A/C=y en C/B=x, dan staat hier y=1/x+1.
Anders gezegd: het punt met coordinaten (C/B,A/C) ligt op de grafiek van y=1/x+1.
In het artikel Mammalian Skull Dimensions and the Golden Ratio worden de volgende gemiddelden van de verhoudingen gerapporteerd: A/C=1.64 ± 0.04) en C/B=1.57 ± 0.10 (de letters zijn anders, maar het gaat om de getallen).
Niet alleen het punt (1.57,1.64) ligt op de grafiek van y=1/x+1 maar ook de punten (1.47,1.68) en (1.67,1.60); deze worden bepaald door de randpunten van de intervallen (1.60,1.68) (voor A/C) en (1.47,1.67) (voor (C/B). Zie het plaatje hieronder.
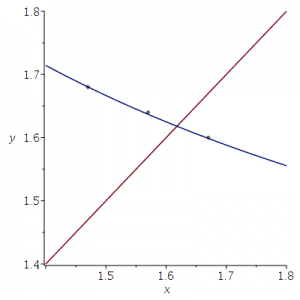
Dit bedoel ik met kloppende getallen: de resultaten horen in ieder geval bij de stituatie waar A=B+C.
Overigens laat ik het aan de lezer om te beoordelen, gezien dit plaatje, in hoeverre deze conclusie gerechtvaardigd is:
In humans, the ratio of the nasioiniac arc over the parieto-occipital arc (NI/BI = 1.64 ± 0.04) and the ratio of the parieto-occipital arc over the frontal arc (BI/NB = 1.57 ± 0.10) are essentially identical and closely approximate Φ (1.618) within 1 standard deviation.
Het snijpunt van de twee grafieken (y=1/x+1 en y=x) is het punt (Φ,Φ), en daar ligt (1.57,1.64) toch nog wel ver vandaan.
Hartslag en bloeddruk
In de referenties van het schedelartikel vond ik de artikelen die hierboven genoemd werden.
Hartslag
Om te beginnen: in Golden Ratio is beating in our heart wordt de Gulden Snede ontdekt in verhoudingen van tijdsintervallen in de hartslag. Een mooi plaatje met een uitleg van alle termen staat op de wikipedia-pagina over het QRS-complex:

De drie grootheden waar het hier om gaat zijn: (A) het R-R-interval (tussen twee opeenvolgende R-en), (B) de systole (samentrekfase), en (C) de diastole (ontspanningfase).
De letters komen overeen met onze eerste paragraaf en met de verhoudingen waar het artikel over gaat.
De resultaten zijn
- A=866 ± 73
- B=333 ± 22
- C=536 ± 66
- C/B=1.611
- A/C=1.618
Deze getallen zijn problematisch.
Ten eerste tellen de gemiddelde waarden niet goed op: A=866 en B+C=869. Dat zou wel moeten als alle metingen goed waren dan geldt A=B+C voor elke meting en dan ook voor de gemiddelden.
Ten tweede: als een van de verhoudingen gelijk is aan Φ dan is de andere dat ook, hier is dat niet zo.
Ten derde: als je, net als in het schedelmetingartikel, de verhoudingen van de gemiddelden neemt kom je op andere getallen uit: 866/536=1.61567 en 536/333=1.6096.
Het zou kunnen zijn dat de gerapporteerde verhoudingen gemiddelden zijn van de verhoudingen per meting maar dan hadden de auteurs dat wel even mogen vermelden.
Voorlopig geloof ik niets van de conclusies van het artikel.
Het lijkt er op dat de individuele verhoudingen wel zijn uitgerekend want het artikel bevat nog een niet-ter-zake-doende grafiek waarin de verhouding C/B is uitgezet tegen de hartslag.

Daar is in ieder geval te zien dat de verhouding C/B behoorlijk variabel is.
Bloeddruk
In het artikel Does systolic and diastolic blood pressure follow Golden Ratio gaat het om de bloeddruk. De grootheden zijn nu: (A) de systolische druk (bovendruk), (C) de diastolische druk (onderdruk), en (B) hun verschil; alle in mm Hg.
| A | C | B | A/C=y | C/B=x | |
|---|---|---|---|---|---|
| etmaal | 137 ± 16 | 86 ± 12 | 51 | 1.59 | 1.69 |
| dag | 140 ± 17 | 89 ± 12 | 51 | 1.57 | 1.75 |
| nacht | 131 ± 18 | 80 ± 13 | 51 | 1.64 | 1.62 |
Wat hier opvalt is dat er voor het verschil geen interval is opgegeven; alsof het bij alle metingen precies 51 mm Hg was (dat geloof ik dus niet). De verhoudingen komen hier wel voort uit de gemiddelden behalve de verhouding C/B in de nacht: 80/51=1.56862. Laat die foute 1.62 nou net de verhouding zijn die het dichtst bij de Gulden Snede ligt.
Ik heb de punten vergeleken met de grafiek van y=1/x+1.
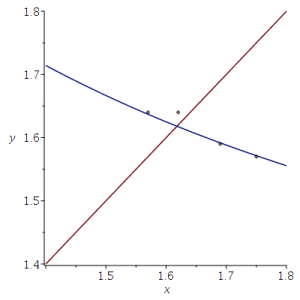
De twee punten rechts horen bij de verhoudingen voor een etmaal en overdag. Het meest linkse punt hoort bij de echte nachtelijke verhoudingen. Het punt dat ruim boven de grafiek ligt hoort bij de gerapporteerde nachtelijke verhoudingen. Ik heb geen idee hoe dat gebeurd kan zijn.





Recent Comments