En tau rund jorden, II

Dette er andre delen av en oversettelse av en artikkel som ble publisert i November 2004 i Pythagoras (et matematisk tidsskrift for unger). Artikkelen finnes også på Engelsk i Half a Century of Pythagoras, en utvalg av artikler publisert av MAA.

Vi strekker en tau helt tettsittende rund jorden, forlenger det lit og drar de opp til den en helt stram. Hvor høyt må vi dra opp tauen? Kan vi uttrykke høyden i lengden vi spleiset inn?

I går vi så at når vi tar en tau som er en meter langre enn jordens omtrekk og drar tauen strammt ved Nordpolen så skal det høyeste punktet være på 121 meter og lit mer. I dag skal vi lage en enkel formel med radiusen og ekstra lengden i som gir en god approksimasjon av høyden.

En effektiv approksimasjon

Her er tegningen fra i går igjen

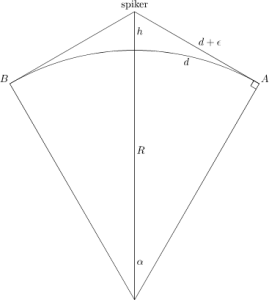
Fra Pythagoras sin læresetning lærte vi at

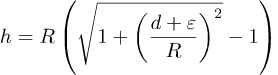
Fra bildet ser vi også at

Dette kan kombineres til denne ligningen

Nå har vi et uttrykk for h som bruker R og α men vi trenger et som bruker ε. Dette må gjøres implisitt fordi α er en løsning av

og der er ingen `pen’ (eller stygg) formel for løsningene.

Som vi så i går er vinkelen α veldi liten (0.006176 radianer). Nå er det slik at α+α³/3 er en veldi bra approksimasjon av tanα. Hvis vi setter dette uttrykket i ligningen så får vi

Også tanα er veldi liten.
Og for x nær 0 har vi √(1+x)≈1+½x; nå kan vi forenkle formelen for h til en approksimasjon

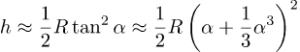
Neste steg er å skrive ut kvadraten

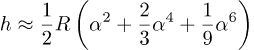
Når vi setter i tallene så får vi Rα²=242.8 m, Rα⁴=0.009 m og Rα⁶=3.5×10^-7 m. Vi derfor kan trygt kaste fjerde og sjette potensene og så får vi denne approksimasjonen for h:

Lit lengre siden fant vi at

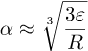
Vi setter det inn i approksimasjonen og får

Nå bruker vi verdien av R og får til slutt

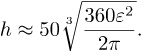
Det flotte med denne formelen er at den gir nesten samme svaret som i går: setter vi inn ε=0.5 så får vi h≈121.4 m igjen.

Oppgav
Sett inn ε=0.005 in formelen vår. Hvor mye forskjeller resultatet fra verdien av h som vi fikk i går?

Exercise
Undersøk hvor bra approksimasjonen √(1+x)≈1+½x er. For eksempel, sammenlign (1+½x)² med 1+x; for hvilken x er forskjellen liten nok til å bli kastet? Er du enig i hvordan approksimasjonen brukes her?

Bemerkning
Vi kan isolere ε i formelen:

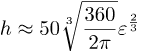
dette gir viktig kvalitativ informasjon: h er omtrent lik en konstant ganger ε^2/3.
Hvis du er kjent med Taylorpolynomer kann det være gøy å finne ut hvor stor feilen er (hvilken potens av ε) i denne approksimasjonen.

Be Sociable, Share!

• 
•