Posted in April 2018
Wat is een verzameling? I
De Wiskunde is doordrenkt van verzamelingen. Nagenoeg elke definitie van een te bestuderen structuur — groep, graaf, interval, … — begint met “een verzameling die …”. De taal en de methoden van de Verzamelingenleer helpen dan ook vaak bij het efficiënt formuleren en noteren van resultaten.
Hierbij gaat men voor het gemak voorbij aan het feit dat de vraag “Wat is een verzameling?” nog niet beantwoord is. Dat klinkt merkwaardig want we herkennen een verzameling wel als we er een zien: postzegels, boeken, vingerhoedjes, …, je kunt het zo gek niet bedenken of iemand heeft er wel een verzameling van.
Echter, in de Wiskunde houden we van precieze definities, zodat op elk moment duidelijk is waar we het over hebben. Hier is een waarschuwing op zijn plaats, mooi geïllustreerd door het volgende citaat
1005. Die Mathematiker sind eine Art Franzosen; redet man mit ihnen, so übersetzen sie es in ihre Sprache, und dann ist es alsobald ganz etwas anderes.
Johann Wolfgang von Goethe,
Maximen und Reflexionen, Nachlass, Über Natur und Naturwissenschaft
Ik heb niet de illusie te weten wat Goethe hier zelf mee bedoelde en door nadere bestudering van zijn is dat wellicht te achterhalen maar ik vind de uitspraak op zichzelf al treffend genoeg. Veel definities van wiskundige begrippen beantwoorden niet aan het idee dat de niet-wiskundige er van heeft.
Hoe zit dat met het begrip `verzameling’? Hoe kijken we daar wiskundig tegenaan. Een van de eersten die een definitie van `verzameling’ formuleerde was Bernard Bolzano.
Einen Inbegriff, den wir einem solchen Begriff unterstellen, bei dem die Anordnung seiner Theile gleichgültig ist (an dem sich also nichts für uns Wesentliches ändert, wenn sich bloss diese ändert) nenne ich eine Menge.
Bernard Bolzano,
Paradoxien des Unendlichen (1851)
Een andere definitie vinden we bij Georg Cantor.
Unter einer ,Menge` verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objecten m unserer Anschauung oder unseres Denkens (welche die ,Elemente` von M genannt werden) zu einem Ganzen.
In Zeichen drücken wir dies so aus:M = {m}
Georg Cantor,
Beiträge zur Begründung der transfiniten Mengenlehre (Erster Artikel) (1895)
Het is, denk ik, geen toeval dat het begrip `Menge’ gedefinieerd werd bij onderzoek naar het begrip `oneindig’. Op dat moment zijn eventueel gegeven relaties tussen de individuen in het geheel van ondergeschikt belang. Op een gegeven moment kies je uit een hele rij synoniemen — collectie, veelheid, Mannigfaltigkeit, aggregate, set, verzameling, … — er eentje en dat wordt dan de naam van het basisbegrip.
Wie de definities nauwkeurig leest ziet dat ze, eigenlijk, niets zeggen: beide gebruiken een synoniem, Inbegriff en Zusammenfassung, als definitie. Daarbij zegt de definitie van Bolzano expliciet en die van Cantor impliciet wat hierboven al is gezegd: bij een verzameling is de onderlinge relatie van de elementen niet van belang. Vlak voor de definitie gaf Bolzano het voorbeeld van een gebroken glas; dat vinden wij iets heel anders dan hetzelfde glas voor het gebroken was omdat de onderlinge relatie tussen de delen verstoord is, als verzameling — atomen, moleculen — is het niet veranderd.
De definities van Bolzano en Cantor hadden ongetwijfeld het doel zo scherp mogelijk af te bakenen over welke zaken er uitspraken gedaan werden. Bolzano nam daarbij een lange aanloop waarvan de definitie een samenvatting was.
Op een naïef niveau kun je met deze afspraken redelijk uit de voeten omdat er niet meer gebeurd is dan dat bekende gehelen nu het predicaat `verzameling’ opgeplakt hebben gekregen. Iets als {1,2,3,4,5} wordt door iedereen herkend als “de verzameling natuurlijke getallen van 1 tot en met 5”. En ook verzamelingen met een beschrijving als {n ∈ N : n ≤ 10100} herkennen we wel, mits we eerst hebben afgesproken dat N de verzameling der natuurlijke getallen voorstelt.
Waar de wiskunde en de dagelijkse praktijk uit elkaar lopen is bij de kleinste verzamelingen: de lege verzameling en de verzamelingen met één element. Als ik zeg dat ik een postzegelverzameling heb en ik laat een album zonder zegels zien dan gelooft niemand mij, ook niet als ik er één laat zien (vlak voor ik hem op een brief plak).
Wiskundig gesproken zouden dat volstrekt legitieme verzamelingen zijn ook al piept de buitenwacht nog zo hard. Bij het werken met en gebruik van verzamelingen komen die kleine verzamelingen zo vaak voor dat het heel vervelend wordt ze iedere keer uit te sluiten van het verzamelingschap. Denk aan vergelijkingen. Heel vaak wordt daar over de oplossingsverzameling gesproken en dat zou ineens niet mogen als er geen of maar één oplossing is? Kom nou!
Maar goed, dit alles gaat nog uit van de opvatting dat we verzamelingen herkennen als we ze zien. Het vertelt ons nog niet wat een verzameling is. Wat de moderne opvatting van verzameling is zien we volgende keer.
Å Bygge Broer
I Abels Tårn på 23. mars hørte jeg et forsøk å forklare hvorfor Robert Langlands fikk tildelt Abelprisen 2018. “Hans program danner broer mellom tallteorien og andre deler av matematikken.” Det ble ikke mye mer diskusjon; det var snakk om `automorfe former’, men bare snakk.
Hvis en ønsker å vite hva Langlands Program handler om så kan enfinne noen innledende artikler på Abelprisens nettsted. I Abels Tårn hører vi også om prisvinneren fra 2016: Andrew Wiles. Wiles sin bevis av Fermats siste theorem er et eksempel på bruk av en bro mellom Tallteorie og Algebraisk Geometri.
Jeg lurte på om det ikke var een liten bro mellom tallteori og geometri (algebraisk eller annerledes) som kunne illustrere hvordan geometri kan hjepe tallteori (eller omvendt).
Her har vi kanskje en, et enkelt spørsmål i talltheorie: fins det to kvadrattall der et er doppelt så stor enn det andre? Det vil si: fins det to naturlige tall, m og n, slik at n2=2×m2?
For dette spørsmålet kan vi bygge en bro til geometrien: vi tegner to kvadrater, et med sidelengde m og et med sidelengde n. og spørsmålet er om vi kan få det til at arealet av det andre kvadratet er to ganger arealet av det første.
Vi kan tegne kvadratene sånn:.
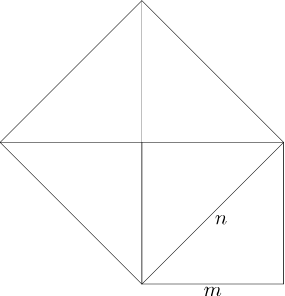
Det er en elementær læresetning at en kan doble arealet av en kvadrat ved å tegne et kvadrat hvilket sidelengde er lik diagonalen in det første kvadratet.
Nå tar vi en rettvinklet trekant med sidelengder m, m og n (halvparten av kvadratet med sidelengder m). Vi danner et punkt z på som deler hypotenusen i to stykker, av lengde m og n-m, og så tegner vi linien gjennom z vinkelrett på hypotenusen og mot siden av trekantet.
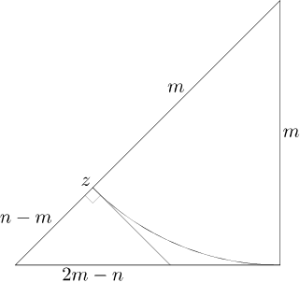
Hypotenusen i det nye trekantet er diagonalen in et kvadrat med sidelengde n-m og derfor vet vi at kvadratet av hypotenusen er lik 2(n-m)2. Når vi bruker at n2=2m2: så får vi
2(n-m)2=2n2-4nm+2m2=4m2-4nm+n2=(2m-n)2
Den nye hypotenusen er altså 2m-n lang.
Dette beviser at det er ikke mulig å finne to naturlige tall m og n som i spørsmålet: hvis det fins to slike tall så kan vi finne andå to slike tall som er mindre. Men for de naturlige tall vet vi: hvis det fins et tall som har en (ønsket) egenskap så fins det et minste tall med denne egenskapen. Så vi kunne ha begynt med det minste tall n slik at det fins et tall m for hvilet vi har n2=2m2 men da er 2m-n et mindre tall med samme egenskapen. Dette motbeviser at en sånn n fins.
Her ser vi, som i beviset til Wiles, at geometrien hjelper å løse et tallteoretisk problem.
Nå er det slik at vårt tallteoretisk problem har en (nogså enkel) tallteoretisk løsning: i kvadraten n2 finner vi et likt antall primfaktorer 2, dobbelt så mange som i n selv. Og i 2 ganger et kvadrat, 2m2, finner vi et odde antall primfaktorer 2, dobbelt så mange som i m selv plus en til. Det betyr at 2m2 er aldri lik n2.
Og mange folk håper at Fermats Siste Teorem har en slik enkel bevis også.

Recent Comments