Bruggen bouwen
In het Noorse radioprogramma Abels Tårn werd op 23 maart een poging gedaan uit te leggen waarom Robert Langlands de Abelprijs 2018 had gekregen. “Hij bouwde bruggen tussen diverse gebieden in de Wiskunde.” Veel verder ging de discussie niet; al viel de kreet `Automorfe Vormen’ nog even.
Voor wie wil weten wat het Langlands Program inhoudt kan op op de website van de Abelprijs wat inleidende artikelen vinden. In het radioprogramma werd nog even verwezen naar een eerdere winnaar Andrew Wiles. Diens bewijs van de Grote Stelling van Fermat is een voorbeeld van het gebruik van zo’n brug tussen Getaltheorie aan de ene oever en Algebraïsche Meetkunde aan de andere.
Ik vroeg me af of er niet een klein bruggetje tussen getaltheorie en meetkunde (algebraïsch of anderszins) bestaat dat als illustratie kan dienen.
Misschien helpt dit, een eenvoudige getaltheoretische vraag: bestaan er twee kwadraten (van natuurlijke getallen) waarvan de ene het dubbele van de andere is? Dat wil zeggen: zijn er twee natuurlijke getallen, m en n, zo dat n2=2×m2?
Je kunt voor dit probleem een brug naar de meetkunde slaan: teken twee vierkanten, een van n bij n en een van m bij m. De vraag is of je m en n zo kunt kiezen dat de oppervlakte van het eerste vierkant twee keer zo groot is als het tweede.
In de meetkundige versie kun je de vierkanten als hieronder tekenen.
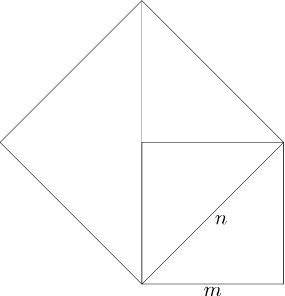
Om een gegeven vierkant in oppervlakte te verdubbelen moet je een vierkant tekenen waarvan de zijden gelijk zijn aan de diagonaal van het eerste vierkant.
Neem nu de rechthoekige driehoek met zijden m, m en n. Pas m af op de schuine zijde en teken de lijn vanuit z loodrecht op de schuine zijde naar de basis.
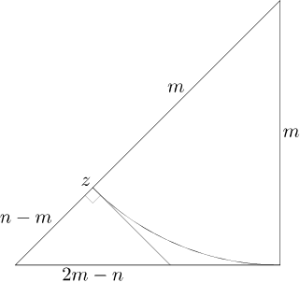
De schuine zijde van de nieuwe driehoek is de diagonaal van een vierkant met zijden n-m en dus geldt dat het kwadraat van die zijde gelijk is aan 2(n-m)2. Schrijf dat uit en gebruik dat n2=2m2:
2(n-m)2=2n2-4nm+2m2=4m2-4nm+n2=(2m-n)2
Dus die schuine zijde is inderdaad 2m-n lang.
Dit laat zien dat het niet mogelijk is natuurlijke getallen m en n te vinden als gewenst: als er twee van die getallen zijn dan kun je twee andere vinden die kleiner zijn. Maar in de natuurlijke getallen geldt: als er een getal met een bepaalde eigenschap bestaat dan is er ook een kleinste getal met die eigenschap. We hadden dus onze m en n zó kunnen kiezen dat n het kleinste getal is waarvoor een m bestaat met n2=2m2 en dan is 2m-n een echt kleiner getal met dezelfde eigenschap. Die tegenspraak laat zien dat zo’n n er in het geheel niet is.
Dus, als in het bewijs van Wiles, heeft de meetkunde geholpen bij het oplossen van een getaltheoretisch probleem.
Overigens heeft het getaltheoretische probleem een eenvoudige getaltheoretische oplossing: in een kwadraat n2 komt de priemfactor 2 een even aantal malen voor, namelijk twee keer zo vaak als in n zelf. En in het dubbele van een kwadraat, 2m2 komt 2 een oneven aantal malen voor: een even aantal maal in m2 plus de ene extra factor 2. Dus 2m2
is nooit gelijk aan n2.
En vele mensen hopen dat de grote stelling van Fermat ook zo’n eenvoudig bewijs heeft.





5 comments
A^n+B^n ongelijk aan C^n
Twee aanpassingen, verschrijvingen
p deler van q^n+r^n
A^n+B^nC^n
Geachte heer Hart,
De grote stelling van Fermat.
Deze stelling kan op eenvoudige wijze worden bewezen.
Gegeven:
(A,B,C,n) paargewijs copriem.
A en C oneven, B even n priem groter dan 2.
Als:
A^n+B^n=C^n dan bestaat er een q deler van A en een r deler van B en een p deler van C en p deler van q^n=r^n,
dan:
(2·(q^(n^2)+r^(n^2))/(p^n+q^n+r^n)=natuurlijk getal.
Als: (2·(q^(n^2)+r^(n^2))/(p^n+q^n+r^n)=natuurlijk getal
dan:
p^n=q^n+r^n.
M.b.v. Oneindige Afdaling volgt A^n+B^nC^n
Met vriendelijke groet,
Karel ten Hoeve
E-mail: karel.ten.hoeve@gmail.com
Dit was een hervertelling van een bewijs dat irrationaal is, met als doel te laten zien hoe meetkunde en getaltheorie op elkaar inwerken.
Heel leuk om te lezen. Maar ik denk direct: m en n verhouden zich als wortel 2, en kunnen dus nooit allebei natuurlijke getallen zijn. Waarom zou dat geen voldoende bewijs zijn?