Posted in September 2017
Tijdrijden in Bergen
Deze week worden in Bergen, Noorwegen, de wereldkampioenschappen wielrennen op de weg gehouden, met vandaag, 20-09-2017, het tijdrijden voor de heren. Het parcours is interessant: een relatief vlakke rit met aan het eind een klim naar de top van Fløyen, een plek met een mooi uitzicht over de stad en de haven.
In de lokale krant Bergens Tidende staat het profiel van de rit getekent, met de laatste drie kilometer nog een keer apart in het onderstaande plaatje.
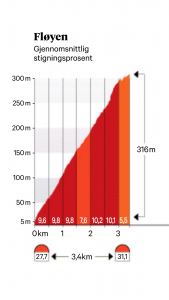
Dat ziet er dramatisch uit, tot je even naar de eenheden kijkt: horizontaal zijn dat kilometers, verticaal gaat het in stappen van 50 meter omhoog. En dat geeft, op zijn zachtst gezegd, een vertekend beeld. Ik heb, bij benadering, het echte profiel even geschetst.
![]()
Dat lijkt niet erg steil en zo van opzij ziet het er niet moeilijk uit; echter, bij wegen met een dergelijke helling staat vaak een waarschuwingsbord voor, juist, een steile helling. Een hellingspercentage van ongeveer 10 % betekent dat er constant met een kracht gelijk aan ongeveer 10 % van het gewicht van jezelf en je fiets tegen je aan geduwd wordt. Naar beneden is dat plezierig al zul je snel zien dat je in je remmen moet knijpen om niet te snel te gaan. Naar boven maak die kracht het fietsen al een stuk moeilijker.
Voor wie wil rekenen: denk maar eens aan de formule F=m×a (kracht is massa maal versnelling). De kracht recht naar beneden is gelijk aan g×m (hier is g de zwaartekrachtsversnelling, daar mochten we op school wel de waarde 10 voor nemen). Hiervan werkt 10 % langs de weg, dus onze F is gelijk aan g×m/10, van school mocht ik daar dus m van maken. Conclusie: de versnelling die we ondervinden als we freewheelend naar beneden gaan is 1 m/s2. Per seconde gaan we dus een meter per seconde sneller. Bereken zelf maar eens hoe snel je dat te link vindt worden.
Een meer dan reële kans?
Op twitter keek Marc van Oostendorp terug naar een blogpost van hemzelf over het woord `reëel’: Hoe reëel is meer dan reëel?. In dat stuk wordt gesproken van reële kansen en van kansen die meer dan reëel zijn. En toen sloeg mijn hoofd een beetje op hol: wat voor kansen zijn dat nou weer?
In de wiskunde wordt met het begrip `kans’ heel anders omgegaan dan in het dagelijks leven. In deze column van Ionica Smeets word de wiskundige opvatting van `kans nul’ vergeleken met de dagelijkse. In het kort: het wiskundige `kans nul’ betekent niet hetzelfde als `dat gebeurt niet’ maar als we horen dat de morgen de kans op regen nul is gaan we er van uit dat het morgen niet zal regenen.
Dat verschil brengt de professionele kansrekenaars er toe het woord `kans’ maar los te laten en het bijna-synonieme `waarschijnlijkheid’ gebruiken.
Maar goed, omdat die termen `kans’ en `waarschijnlijkheid’ buiten de wiskunde nagenoeg synoniem zijn kan men zich afvragen wat we aanmoeten met `reële kansen’ en `meer dan reële kansen’.
Wat het eerste betreft: `reële kansen’ is een pleonasme. De kans/waarschijnlijkheid van een gebeurtenis is, per definitie, een reëel getal uit het interval [0,1].
Maar nu het tweede, `meer dan reële kansen’. Wat moeten we daar als wiskundigen mee? Je zou kunnen denken een waarschijnlijkheden met waarden buiten de reële getallen. Is dat mogelijk? Zou je complexwaardige kansen kunnen hebben of zelf quaternion-waardige?
Als je naar de Axioma’s van Kolmogoroff kijkt lijkt het niet: de eerste eis is dat P(A)≥0 voor elke gebeurtenis. Aan de andere twee eisen is met complex- of quaternion-waardige kansen wel te voldoen; er is een goed ontwikkelde theorie van maten met waarden in de complexe getallen of in de quaternionen. Met een beetje goede wil kun je in dit geval een kansmaat definiëren als eentje die alleen waarden in de eenheidsbol aanneemt. De vraag is natuurlijk wat je je dan moet voorstellen bij negatieve of een zuiver imaginaire waarschijnlijkheid, maar we kunnen er in ieder geval mee rekenen. En, wie weet, het zou niet de eerste keer zijn dat zulk wiskundig speelgoed een toepassing vindt.
Er is nog een andere manier om kansen `meer dan reëel’ te maken en dat heeft, onder meer, te maken met die `kans nul’ van hierboven. Denk, bijvoorbeeld, aan de uniforme kansverdeling op het interval [0,1]. Deze kansverdeling beschrijft wat er gebeurt als je willekeurig pijltjes in dat interval gooit: de kans dat je het interval [⅓,⅔] raakt is gelijk aan ⅓ en in het algemeen: elk interval (a,b) heeft raakkans b-a. Het gevolg van deze afspraak is dat elk punt raakkans nul heeft. Echter, als je een pijltje in het interval gooit dan raak je een punt, ook al had je kans nul dat punt te raken. Dit is waar het in de column van Ionica Smeets om ging: wiskundig betekent `kans nul’ dus niet hetzelfde als `onmogelijk’.
Wat sommige mensen hierbij ook een beetje stoort is dat kansen niet altijd goed opgeteld kunnen worden: elk punt heeft raakkans nul en als we al die raakkansen optellen krijgen we weer nul, toch? Maar die som zou gelijk moeten zijn aan de kans dat je het interval [0,1] raakt en die is toch gelijk aan 1. Daarnaast is het ook nog zo dat niet elke deelverzameling van [0,1] een welgedefinieerde raakkans heeft. In de praktijk is dat allemaal niet zo erg: het gaat bij de berekeningen vrijwel nooit om individuele punten maar om verzamelingen, en die verzamelingen hebben hebben vaak beschrijvingen waaraan meteen te zien is dat ze een welbepaalde raakkans moeten hebben.
Wat te doen? Je kunt in het model van Solovay gaan werken; daar heeft elke verzameling een welgedefinieerde raakkans. Echter, de optelwet heb je daar nog steeds niet, en die kun je ook niet krijgen zolang je eist dat je raakkansen reële getallen zijn. En hier komen de meer dan reële kansen in beeld.
In dit artikel (ook hier te vinden) ontwikkelden Vieri Benci, Leon Horsten, en Sylvia Wenmackers een waarschijnlijkheidsrekening met waarden in het interval [0,1] van een veel grotere getallenverzameling dan R, maar die er wat elementaire algebra betreft niet van te onderscheiden is. Het onderscheid zit hem in de rijkheid van de verzameling en de mogelijkheid een heleboel oneindige sommen zinvol te kunnen behandelen. De raakkans van een enkel punt van het gewone interval [0,1] is positief maar kleiner dan elk `normaal’ positief reëel getal en dat maakt die kans `meer dan reëel’; ook de verzamelingen die geen welbepaalde raakkans hadden krijgen er nu een, maar ook die kansen zijn `meer dan reëel’.

Recent Comments