Posts in category uit het ongerijmde
Mathsplaining
Gisteren gebruikte Aafke Romeijn in een tweet de frase mansplaining tot de macht oneindig. Ik kon nog net virtueel op mijn tong bijten maar nu moet ik toch even aan het mathsplainen.
Dat “tot de macht oneindig” klinkt wel indrukwekkend maar de kans is groot dat je er niet mee bereikt wat je wilt. Want wat betekent “tot de macht oneindig” eigenlijk? Wiskundig dan. En wat betekent “oneindig”? In dit geval zullen we het maar op het ∞ van de Analyse houden. Dan betekent “mainsplaining tot de macht oneindig” niets anders dan “de limiet van mainsplainingn voor n naar ∞”.
OK, maar dan moeten we dus eerst betekenis hechten aan “mansplaining-kwadraat”,
“mansplaining tot de derde macht”, … en vervolgens het gedrag van die machten van mansplaining bestuderen. Tsja, en dan komt het: hoe vermenigvuldig je mansplaining met zichzelf? Wiskundig betekent het woord niets maar we kunnen wat vermenigvuldigbare zaken langslopen.
We kunnen getallen vermenigvuldigen, en dus ook machtsverheffen. Maar dan komt het: is mansplaining negatief? Voor velen wel, denk ik. Jammer dan, maar dan is het kwadraat positief, de derde macht negatief, de vierde macht positief, … dan kun je het schudden: de limiet bestaat niet. Tenzij, …, je vindt dat mansplaining eigenlijk wel zielig is en weinig waarde heeft, zeg absolute waarde kleiner dan 1. Dan convergeren die machten naar 0 en dan is mansplaining tot de macht oneindig dus gelijk aan 0. Ik weet niet of dat Aafke Romeijn voor ogen stond.
Mansplaining is natuurlijk irreëel en irrationaal; dat lijkt wiskundig niet goed te gaan maar je kunt het interpreteren als “een complex getal met irrationaal argument”. Wiskundigen zien hier meteen een woordspeling: het woord `argument’ heeft in de wereld van de complexe getallen zijn geheel eigen betekenis. Dan leidt machtsverheffen tot een duizeligmakend ronddraaien; het hangt van de absolute waarde af of dit naar 0 convergeert, of naar ∞, of zonder limiet de eenheidscirkel blijft rondlopen. (Om andere mathsplainers de wind uit de zeilen te nemen: dat argument is een irrationaal veelvoud van π.)
Een mansplainer projecteert zijn eigen meningen en gedachten op hetgeen hij aan het mansplainen is. Dat leidt tot een wat merkwaardige situatie: wiskundig is het kwadraat van een projectie de projectie zelf. En dus is elke macht van mansplaining gelijk aan mansplaining zelf, met als conclusie dat mansplaining tot de macht oneindig gewoon mansplaining is. Eigenlijk wel een mooie conclusie: mansplaining is al zo erge flauwekul dat het zijn eigen oneindige macht is.
Bruggen bouwen
In het Noorse radioprogramma Abels Tårn werd op 23 maart een poging gedaan uit te leggen waarom Robert Langlands de Abelprijs 2018 had gekregen. “Hij bouwde bruggen tussen diverse gebieden in de Wiskunde.” Veel verder ging de discussie niet; al viel de kreet `Automorfe Vormen’ nog even.
Voor wie wil weten wat het Langlands Program inhoudt kan op op de website van de Abelprijs wat inleidende artikelen vinden. In het radioprogramma werd nog even verwezen naar een eerdere winnaar Andrew Wiles. Diens bewijs van de Grote Stelling van Fermat is een voorbeeld van het gebruik van zo’n brug tussen Getaltheorie aan de ene oever en Algebraïsche Meetkunde aan de andere.
Ik vroeg me af of er niet een klein bruggetje tussen getaltheorie en meetkunde (algebraïsch of anderszins) bestaat dat als illustratie kan dienen.
Misschien helpt dit, een eenvoudige getaltheoretische vraag: bestaan er twee kwadraten (van natuurlijke getallen) waarvan de ene het dubbele van de andere is? Dat wil zeggen: zijn er twee natuurlijke getallen, m en n, zo dat n2=2×m2?
Je kunt voor dit probleem een brug naar de meetkunde slaan: teken twee vierkanten, een van n bij n en een van m bij m. De vraag is of je m en n zo kunt kiezen dat de oppervlakte van het eerste vierkant twee keer zo groot is als het tweede.
In de meetkundige versie kun je de vierkanten als hieronder tekenen.
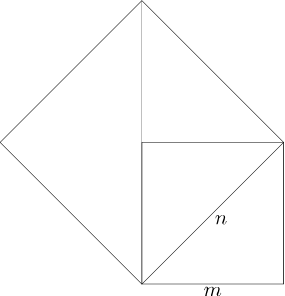
Om een gegeven vierkant in oppervlakte te verdubbelen moet je een vierkant tekenen waarvan de zijden gelijk zijn aan de diagonaal van het eerste vierkant.
Neem nu de rechthoekige driehoek met zijden m, m en n. Pas m af op de schuine zijde en teken de lijn vanuit z loodrecht op de schuine zijde naar de basis.

De schuine zijde van de nieuwe driehoek is de diagonaal van een vierkant met zijden n-m en dus geldt dat het kwadraat van die zijde gelijk is aan 2(n-m)2. Schrijf dat uit en gebruik dat n2=2m2:
2(n-m)2=2n2-4nm+2m2=4m2-4nm+n2=(2m-n)2
Dus die schuine zijde is inderdaad 2m-n lang.
Dit laat zien dat het niet mogelijk is natuurlijke getallen m en n te vinden als gewenst: als er twee van die getallen zijn dan kun je twee andere vinden die kleiner zijn. Maar in de natuurlijke getallen geldt: als er een getal met een bepaalde eigenschap bestaat dan is er ook een kleinste getal met die eigenschap. We hadden dus onze m en n zó kunnen kiezen dat n het kleinste getal is waarvoor een m bestaat met n2=2m2 en dan is 2m-n een echt kleiner getal met dezelfde eigenschap. Die tegenspraak laat zien dat zo’n n er in het geheel niet is.
Dus, als in het bewijs van Wiles, heeft de meetkunde geholpen bij het oplossen van een getaltheoretisch probleem.
Overigens heeft het getaltheoretische probleem een eenvoudige getaltheoretische oplossing: in een kwadraat n2 komt de priemfactor 2 een even aantal malen voor, namelijk twee keer zo vaak als in n zelf. En in het dubbele van een kwadraat, 2m2 komt 2 een oneven aantal malen voor: een even aantal maal in m2 plus de ene extra factor 2. Dus 2m2
is nooit gelijk aan n2.
En vele mensen hopen dat de grote stelling van Fermat ook zo’n eenvoudig bewijs heeft.
Tien getallen rond een tafel
Op de Wisfaq stond laatst weer een aardige vraag:
Natuurlijke getallen van 1 tot en met 10 zijn geordend in een willekeurige volgorde rond een cirkel. Je kan steeds (dus in een cirkel is er minstens 1 geval) 3 opeenvolgende getallen vinden waarvoor de som groter is dan 17.
Hoe zou je zoiets aanpakken? Meestal kun je wel iets over die sommen zeggen waardoor blijkt dat er één (of meer) over een bepaalde grens moet gaan, bijvoorbeeld als de som van al die sommen groot moet zijn.
In dit geval kunnen de tien sommen bij elkaar optellen; dan tellen we elk getal 1, 2, …, 9, 10 driemaal mee dus we krijgen als totaal 3×(1+2+…+9+10)=3×55=165.
Dat betekent dat niet alle sommen kleiner dan 17 kunnen zijn, want dan zou hun totaal niet groter zijn dan 10×16=160. Het eerste succes is binnen: we zien vrij goedkoop dat tenminste één drietal een som van 17 of meer moet hebben.
Vervolgens heb ik een paar vellen kladpapier gebruikt om de getallen zo rond de tafel te plaatsen dat alle sommen niet groter waren dan 17. Waarom? Voor mij is het zo dat als ik zoiets vaak genoeg mis zie lopen ik een idee krijg hoe te bewijzen dat het gevraagde waar is: de reden van het mislopen is soms een sleutel tot een bewijs.
In dit geval bleek het lastig het gemiddelde van de sommen in de buurt van 16,5 te houden, dus ging ik kijken hoe dat gemiddelde gelijk kon zijn aan 16,5 terwijl alle sommen niet groter dan 17 mochten zijn.
Na wat proberen bleek dat ten minste vijf van de sommen gelijk aan 17 moeten zijn; immers, bij vier (of minder) sommen gelijk aan 17 zijn de andere zes (of meer) sommen niet groter dan 16 en dus zou het totaal niet groter zijn dan 4×17+6×16=164, en dat is net te klein.
Daarnaast bleek dat er ook maar ten hoogste vijf sommen gelijk aan 17 konden zijn. Dat was zo duidelijk dat ik het eerst over het hoofd zag: neem vier getallen op een rij: x1, x2, x3, x4.
Omdat x1≠x4 volgt dat x1+x2+x3≠x2+x3+x4. Van elk tweetal naast elkaar liggende sommen is er dus hooguit één gelijk aan 17.
Als we de tafel rondlopen zien we dus nooit twee sommen gelijk aan 17 naast elkaar; dat betekent dat we niet meer dan vijf maal een 17 zullen zien.
Nu weten we dat er precies vijf sommen gelijk zijn aan 17, maar dan moeten de andere vijf sommen gelijk zijn aan 16 (om het totaal op 165 te houden) en de sommen 17 en 16 komen dus om en om voor.
Loop nu de tafel rond en noem de getallen die je ziet x1, x2, … en begin op een plek waar x1+x2+x3=17. Dan moet vervolgens gelden
- x2+x3+x4=16, en
- x3+x4+x5=17, en
- x4+x5+x6=16, en
- x5+x6+x7=17.
Trek de tweede vergelijking van de eerste af, je ziet x1-x4=1.
Trek de vierde vergelijking van de vijfde af, je ziet x7-x4=1.
Maar nu volgt x1=x7 en dat kan niet want we hadden tien verschillende getallen rond de tafel gezet.
Conclusie: elke poging alle tien de sommen kleiner dan of gelijk aan 17 te houden zal falen. Hoe je de getallen ook neerzet, er is een som die groter is dan 17.
In de Wiskunde heet zoiets een (niet-constructief) existentiebewijs: we laten zien dat iets moet voorkomen maar er is geen recept dat het gewenste verschijnsel aanwijst. Het bewijs geeft (slechts) aan hoe een poging zal stranden: je moet vijf keer 17 als som hebben, en vijf keer 16, en die moeten om en om voorkomen en dan loopt het echt mis: twee verschillende getallen moeten gelijk zijn.
Opdracht.
Om te puzzelen: is er een verdeling met alle sommen niet groter dan 18? Ik heb het nog niet geprobeerd.

Recent Comments