Å Bygge Broer

I Abels Tårn på 23. mars hørte jeg et forsøk å forklare hvorfor Robert Langlands fikk tildelt Abelprisen 2018. “Hans program danner broer mellom tallteorien og andre deler av matematikken.” Det ble ikke mye mer diskusjon; det var snakk om `automorfe former’, men bare snakk.

Hvis en ønsker å vite hva Langlands Program handler om så kan enfinne noen innledende artikler på Abelprisens nettsted. I Abels Tårn hører vi også om prisvinneren fra 2016: Andrew Wiles. Wiles sin bevis av Fermats siste theorem er et eksempel på bruk av en bro mellom Tallteorie og Algebraisk Geometri.

Jeg lurte på om det ikke var een liten bro mellom tallteori og geometri (algebraisk eller annerledes) som kunne illustrere hvordan geometri kan hjepe tallteori (eller omvendt).

Her har vi kanskje en, et enkelt spørsmål i talltheorie: fins det to kvadrattall der et er doppelt så stor enn det andre? Det vil si: fins det to naturlige tall, m og n, slik at n²=2×m²?
For dette spørsmålet kan vi bygge en bro til geometrien: vi tegner to kvadrater, et med sidelengde m og et med sidelengde n. og spørsmålet er om vi kan få det til at arealet av det andre kvadratet er to ganger arealet av det første.
Vi kan tegne kvadratene sånn:.

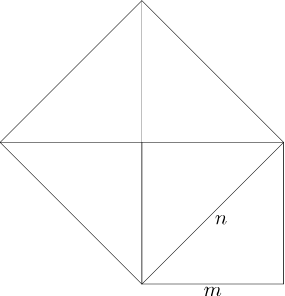
Det er en elementær læresetning at en kan doble arealet av en kvadrat ved å tegne et kvadrat hvilket sidelengde er lik diagonalen in det første kvadratet.
Nå tar vi en rettvinklet trekant med sidelengder m, m og n (halvparten av kvadratet med sidelengder m). Vi danner et punkt z på som deler hypotenusen i to stykker, av lengde m og n-m, og så tegner vi linien gjennom z vinkelrett på hypotenusen og mot siden av trekantet.

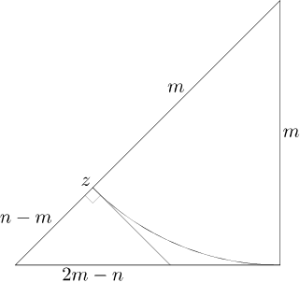
Hypotenusen i det nye trekantet er diagonalen in et kvadrat med sidelengde n-m og derfor vet vi at kvadratet av hypotenusen er lik 2(n-m)². Når vi bruker at n²=2m²: så får vi

2(n-m)²=2n²-4nm+2m²=4m²-4nm+n²=(2m-n)²

Den nye hypotenusen er altså 2m-n lang.

Dette beviser at det er ikke mulig å finne to naturlige tall m og n som i spørsmålet: hvis det fins to slike tall så kan vi finne andå to slike tall som er mindre. Men for de naturlige tall vet vi: hvis det fins et tall som har en (ønsket) egenskap så fins det et minste tall med denne egenskapen. Så vi kunne ha begynt med det minste tall n slik at det fins et tall m for hvilet vi har n²=2m² men da er 2m-n et mindre tall med samme egenskapen. Dette motbeviser at en sånn n fins.

Her ser vi, som i beviset til Wiles, at geometrien hjelper å løse et tallteoretisk problem.

Nå er det slik at vårt tallteoretisk problem har en (nogså enkel) tallteoretisk løsning: i kvadraten n² finner vi et likt antall primfaktorer 2, dobbelt så mange som i n selv. Og i 2 ganger et kvadrat, 2m², finner vi et odde antall primfaktorer 2, dobbelt så mange som i m selv plus en til. Det betyr at 2m² er aldri lik n².

Og mange folk håper at Fermats Siste Teorem har en slik enkel bevis også.

Be Sociable, Share!

• 
•