Een `rekenprobleem’
Er gaat weer een vraag het internet rond en de discussies lopen weer hoog op. Hier is de som

De meest gegeven antwoorden zijn 9 en 1; die komen van de volgende twee interpretaties van 6÷2(1+2):
- 6÷2×(1+2), gelezen van links naar rechts, dus 6÷2 bepalen en dan vermenigvuldigen met (1+2)
- 6÷(2×(1+2)), dus eerst 2×(1+2) bepalen en dan 6 daar door delen
Welk van de twee is de juiste? Eigenlijk geen van beide omdat het hier om een afkorting gaat waarvan niet duidelijk is hoe die gelezen moet worden.
Hoe dat zo? Welnu, in de (elementaire) rekenkunde hebben we een paar bewerkingen: optellen aftrekken, vermenigvuldigen, en delen. Als we een som opschrijven dan kunnen we die ondubbelzinnig houden door middel van haakjes: (1+2)×3 betekent iets anders dan 1+(2×3). Als we heel strikt te werk gaan moeten we zelfs ((1)+(2))×(3) en (1)+((2)×(3)) schrijven; de reden is dat + en × twee argumenten nemen en door (al) die haakjes word precies duidelijk wat die argumenten zijn.
De mens is lui en wil al die haakjes niet opschrijven en daarom is bedacht/afgesproken dat × en ÷ sterker binden dan + en -, dus 1+2×3=7 omdat we hebben afgesproken dat 2×3 eerst moet worden bepaald en dan pas de optelling. Wat als er even sterk bindende symbolen achter elkaar staan? Van links naar rechts werken zeggen de officiële voorschriften (pagina 20), dus 4÷2×4=8: eerst 4÷2=2 en dat vermenigvuldigen met 4; er staan dus impliciete haakjes: (4÷2)×4.
Maar de mens is nog luier en heel vaak wordt een × weggelaten, bijvoorbeeld in onze som: 2(1+2) staat voor 2×(1+2). Als we die × weer invoegen en de regel “van links naar rechts” volgen komen we uit op 9. Echter, en daar ontstaat de verwarring, sommige mensen vinden dat een weggelaten × sterker bindt dan een expliciete × of ÷; dat is niet een officiële afspraak maar een ingesleten gewoonte. En dan lezen we de som als 6÷(2×(1+2)), met als uitkomst 1.
Wat is de oplossing? Wat mij betreft: de vraag terugkaatsen met “Wat bedoel je?” Als ik zou moeten kiezen dan toch maar het eerste antwoord: × invoegen en dan van links naar rechts werken.
Hieronder een paar antwoorden van rekenprogramma’s en rekenmachienes.
Het beste antwoord komt van het programma bc:
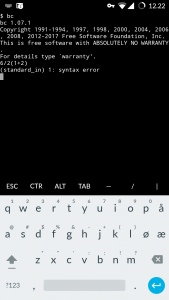
De QAMA-calculator doet gewoon niks; als ik de som intik gaat de cursor weer naar het begin van de regel.
Maple lijkt (1+2) gewoon te negeren
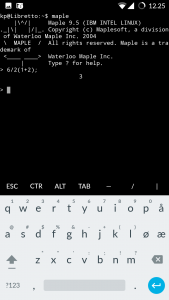
De calculator in mijn telefoon (Android) geeft 9 als antwoord; onderweg wordt 6÷2 uitgerekend, en (1+2) leidt tot een vermenigvuldiging.
En als je niet van haakjes houdt kun je altijd nog dc gebruiken of een andere calculator die met `reverse Polish notation’ werkt:
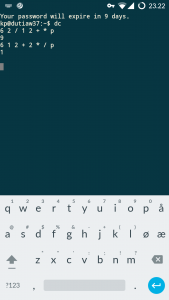
Het echte verhaal
En voor wie echt tot op de bodem wil gaan: delen bestaat niet, 6÷2 is een afkorting van 6×2-1, waarbij 2-1 de multiplicatieve inverse van 2 is (2-1 is een afkorting voor “dat getal, x, met de eigenschap dat 2×x=1”).
De vraag is dus of de som vraagt naar 6×2-1×(1+2) of naar 6×(2×(1+2))-1.
En eigenlijk zijn × en + ook afkortingen, in de echte officiële wiskunde zouden we alles in gewone functienotatie op moeten schrijven: v(a,b) in plaats van a×b, o(a,b) in plaats van a+b, en i(a) in plaats van a^{-1}. De mogelijke interpretaties van de som worden dan respectievelijk v(v(6,i(2)),o(1,2)) en v(6,i(v(2,o(1,2)))).





Recent Comments