Een `wiskundig’ probleem
Op internet doet de volgende opgave de ronde
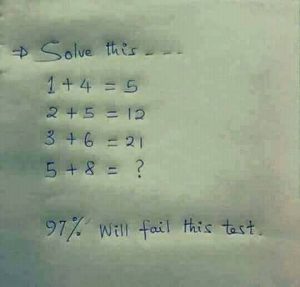
Ik ben persoonlijk geen fan van dit soort `sommen’ omdat de taak niet is te achterhalen wat *de* wetmatigheid achter de gegevens is, want een unieke wet is er niet, maar de wetmatigheid die in het hoofd van de opsteller zat. Mijn standaardantwoord is: 0 (of anders 42, het universele antwoord uit The Hitch-hikers Guide to the Galaxy).
Is er iets zinnigs over een opgave als deze te zeggen? Laten we eens kijken.
Om te beginnen: de + heeft duidelijk niet de functie van optelling. Dat bracht velen er toe het door een ander symbool te vervangen, @ bijvoorbeeld.
De vraag is dan: is er een bewerking @ die voor elk paar natuurlijke getallen m en n een natuurlijk getal m@n produceert en wel zo dat 1@4=5, 2@5=12 en 3@6=21? En zo ja, wat is dan 5@8?
Voor een wiskundige is het antwoord duidelijk: afgezien van die drie eisen kunnen we doen wat we willen, dus het antwoord is ja en 5@8 kan elk getal zijn.
Bijvoorbeeld: definieer m@n=0, behalve in de voorgeschreven drie gevallen; dat rechtvaardigt mijn standaardantwoord. Als we apart 5@8=42 definieren wordt het universele antwoord van Deep Thought correct.
De meeste mensen verwachten niet een antwoord als boven maar een *formule*; één of andere uitdrukking met m en n er in die `voorspelt’ wat 5@8 moet zijn. Dat soort formules zijn er te over.
Als je goed kijkt zijn de drie gegevens van de vorm m@(m+3)=x, dus het zou
kunnen dat de bewerking een flauwe is die alleen van de eerste coördinaat
afhangt.
Er zijn drie waarden gegeven en die kunnen met behulp van een kwadratische uitdrukking als functie van m alleen gegeven worden.
Ga maar na dat m@n=m*m+4m aan de drie eisen voldoet (vul m=1,2,3 in). Dat geeft het op internet meest gegeven antwoord op de vraag: 5@8=25+20=45.
Met een kleine truc kun je oneindig veel formules maken die aan de drie eisen voldoen, maar die voor 5@8 telkens een andere uitkomst opleveren. Die truc komt er op neer dat je iets maakt dat voor 1, 2, en 3 de waarde nul oplevert en voor andere natuurlijke getallen niet, bijvoorbeeld (m-1)(m-2)(m-3).
Nu kunnen we oneindig veel formules opschrijven die allemaal aan de gegevens voldoen maar die voor 5@8 telkens iets anders opleveren: neem een vaste k en definieer m@n=m*m+4m + k(m-1)(m-2)(m-3).
Met wat puzzelen zijn er vast formules te maken die voor 5@8 elke waarde kunnen produceren die je maar wilt; ik zou zeggen: aan het werk.
Hier is alvast een voorbeeld.
![]()
Deze geeft 5@8=4754660328285.
Voor wie wil weten of het rijtje 5, 12, 21 nog natuurlijke uitbreidingen heeft kan ik de On-line Encyclopedia of Integer Sequences aanbevelen: vul het rijtje in het zoekveld in om te zien wat er allemaal te vinden is.





Comments are closed.