Posts in category tellen
Lariekoek? I
Dit is de vierde in een korte serie blogposts naar aanleiding van een discussie op twitter over dit stuk op Neerlandistiek.nl van Marc van Oostendorp dat zelf weer een reactie op dit artikel van Paul Postal was. In de eerste post kwalificeerde ik een opmerking uit het stuk van Postal als lariekoek. Daar gaat deze post over.
De opmerking van Postal betreft de grootte van de `collectie’ van alle boeken in een taal. Die collectie is niet alleen oneindig groot, niet alleen overaftelbaar, maar zelfs groter dan elke denkbare verzameling. Voor (een idee van) het bewijs van deze bewering verwijst Postal naar het artikel Sets and Sentences en een boek, The Vastness of Natural Languages, beide geschreven door hemzelf en D. Terrence Langendoen.
Ik heb wat met verzamelingen en wilde daarom wel eens zien waarom de collectie boeken in een Natuurlijke Taal zo groot moest zijn. Het boek heb ik niet te pakken kunnen krijgen maar deze recensie beweert dat de kern van de inhoud al in het artikel staat. laten we dat artikel dan maar eens bekijken.
Het artikel bestaat uit drie delen: een korte inleiding, een deel waarin “naar analogie met Cantors’s resultaten” wordt beargumenteerd dat de zinnen in een natuurlijke taal geen verzameling vormen, en een deel met conclusies.
Dat tweede deel begint met wat definities die het beschrijven van constructies van nieuwe `zinnen’ uit oude mogelijk moeten maken. Het hoofdingrediënt is dat van een conjunct, dat is een eenheid die bestaat uit een connectief en een deelconjuct. Die conjuncties kunnen in/tot `co-ordinate compound constituents’ samengevoegd worden. Zo’n co-ordinate compound moet wel echt `compound’ zijn en dus uit ten minste twee conjuncten gevormd worden.
Vervolgens spreken de schrijvers af hoe uit een verzameling U van constituents een co-ordinate compound constituent T gemaakt kan worden; of beter: hoe we kunnen zien dat T uit U gemaakt is. Elke conjuct in T heeft een element van U als deelconjunct, elk element van U is deelconjunct van precies één conjuct van T, en de conjuncten in T zijn geordend (daarover later meer).
In dit geval is T een `co-ordinate projection‘ van U, en U is de `projection set van T. Let op het gebruik van `een’ en `de’ in de vorige zin.
Ik kan begrijpen dat dit allemaal nogal abstract overkomt en ik moest het zelf een paar keer lezen voor ik dacht door te hebben wat er aan de hand is. Achter al die termen zitten plaatjes als het onderstaande verscholen:

De verzameling U bestaat uit de constituents `Marc’ en `KP’; uit elk element van U kunnen we een conjunct maken door er een connectief aan vast te plakken. Dat connectief kan leeg zijn, zoals bij `Marc’ omdat, bijvoorbeeld, je aan het begin van een zin geen voegwoord gebruikt en toch iets nodig hebt om je conjuct te markeren. Daar nemen we dan ∅ maar voor. In de woorden van Langendoen en Postal: C1 en C2 zijn de dochters van T, die zusters zijn elk een conjuct, bestaande uit een connectief en een deelconjuct.
De hoofdaanname, of het hoofdaxioma, is nu dat elke verzameling constituents tot een co-ordinate compound constituent gevormd kan worden. De (co-ordinate compound) constituents waar we het verder over zullen hebben zijn gewoon zinnen, en daarom zal ik ze verder ook maar zo noemen.
Om te beginnen maken we oneindig veel zinnen:
- De reële rechte is overaftelbaar
- Ik weet dat de reële rechte overaftelbaar is
- Ik weet dat ik weet dat de reële rechte overaftelbaar is
- Ik weet dat ik weet dat ik weet dat de reële rechte overaftelbaar is
- …
Niet erg opwindende zinnen maar daar gaat het niet om: er is een duidelijke procedure die voor elk natuurlijk getal n een zin Z(n) construeert. Dit is een voorbeeld van een recursieve definitie: als we een beginobject beschrijven en een recept aangeven om elk volgende object te maken dan beschouwen we de constructie als voltooid.
Voor elke deelverzameling U van deze verzameling {Z(n):n∈N} van zinnen bestaat er dus een zin waarvan de deelconjucten precies de zinnen uit U zijn. Dat geeft ons dan overaftelbaar veel zinnen.
Daarmee is het hek van de dam: we kunnen blijven doorgaan en elke deelverzameling van de nieuwe verzameling zinnen weer samensmeden tot een nieuwe zin. En weer, en weer, en weer, …
De conclusie van Langendoen en Postal is nu dat alle zinnen die we zo kunnen maken geen verzameling vormen. Hier komt de analogie met Cantor’s resultaten om de hoek kijken. Cantor bewees namelijk dat elke verzameling strikt meer deelverzamelingen heeft dan elementen. Als je dit toepast op `de verzameling van alle verzamelingen’ kom je in de knoop: de elementen van die `verzameling’ zijn precies zijn deelverzamelingen, maar dat kan niet omdat er meer deelverzamelingen dan elementen zijn. De entiteit `de verzameling van alle verzamelingen’ bestaat dus niet.
Dezelfde redenering is nu van toepassing op `de verzameling van alle zinnen in een natuurlijke taal’: elke deelverzameling bepaalt een zin en verschillende deelverzamelingen bepalen verschillende zinnen en dat druist in tegen de conclusie van Cantor: altijd strikt meer deelverzamelingen dan elementen.
Waarom Lariekoek?
Waarom denk ik dat dit lariekoek is? Dat heeft vooral te maken met de manier waarop Langendoen en Postal hun `bewijs’ presenteren. Daar is wiskundig veel op af te dingen. Maar deze post is al behoorlijk lang en ik bewaar mijn wiskundige opmerkingen, bijvoorbeeld over de bovengenoemde ordeningen daarom maar voor deel twee.
Getallen bestaan (eigenlijk) niet
Dit is de derde in een korte serie blogposts naar aanleiding van een discussie op twitter over dit stuk op Neerlandistiek.nl van Marc van Oostendorp dat zelf weer een rectaie op dit artikel van Paul Postal was. De eerdere delen staan hier en hier.
Tussen al die tweets maakte ik de volgende opmerkingen:
Daar komt nog bij dat `getal' als aantal’ strikt genomen gedefinieerd moet worden; verzamelingen hebben geen intrinsiek `aantal elementen'. Boeken zijn inderdaad eerder stellingen. https://t.co/Mjjth2qDKd
— (((K P Hart))) (@hartkp) October 15, 2019
Daar wil ik het vandaag even over hebben. Wat zijn getallen eigenlijk? Die vraag werd zelfs op de Nationale Wetenschapsagenda gesteld en ik heb daar al eens een antwoord op gegeven. Ik wil dat hier wat uitgebreider doen.
Getallen
Om te beginnen: in de discussie en de stukken ging het over natuurlijke getallen en die werden vereenzelvigd met hun decimale schrijfwijze. Dat is, in deze tijd, heel natuurlijk: afgezien van jaartallen in Romeinse notatie op gevels van gebouwen (en als paginanummers in boeken vóór de echte inhoud begint) zien we getallen eigenlijk alleen opgeschreven met behulp van de indo-arabische cijfers en de positionele schrijfwijze.
Gegeven deze vereenzelviging is er wel iets te zeggen voor het idee dat boeken en getallen iets gemeen hebben: rijen symbolen met een welgedefinieerde inhoud.
Aan de andere kant: getallen zijn in zekere zin absoluut: ze zijn bestand tegen vertalingen. Twaalf, twelve, douze, tolv, dvanást’, teyan-a-bub, … verwijzen allemaal naar exact dezelfde hoeveelheid streepjes: ||||||||||||.
Als ik een stuk tekst van mezelf in het Engels vertaal is die exactheid weg. Sommige nederlandse woorden en uitdrukkingen doen het niet zo goed in letterlijke vertaling (“laat maar” versus “let but”) en een equivalent-bij-benadering is slechts dat: een benadering. Vergelijk deze twee stukken over de Gulden Snede maar: nederlands versus engels.
Meer, minder, even veel
Maar goed, terug naar de vraag over de aard, of het bestaan, van getallen. Ik denk/vind dat getallen, in de zin van aantallen, niet bestaan.
“Maar we tellen toch dagelijks dingen”, hoor ik u zeggen. Inderdaad, maar de zaken die we daarbij gebruiken zijn bedacht, ze bestaan niet in het wild. Ooit `het getal dat wij in het Nederlands drie noemen’ gezien? En hierbij wel de gebruikelijke notaties loslaten, het symbool 3 telt niet, en III ook niet, en γ’ ook niet.
Maar er is meer: in de verzamelingenleer is het na invoering van de bekende soorten afbeeldingen, injectief, surjectie, en bijectie een koud kunstje te definiëren wanneer de ene verzameling minder, meer, of even veel elementen heeft als een andere. Kleine kinderen weten dat al heel snel, en zonder tellen: haal uit beider zakje snoepjes telkens tegelijkertijd één snoepje. Het zakje dat het eerst leeg is bevatte minder snoepjes dan het andere en gelijk leegraken betekent even veel. Probeer het zelf maar eens: neem twee lepels hagelslag en zoek zo uit welke lepel de meeste korrels heeft.
Maar als je in de verzamelingen een antwoord wilt geven op de vraag “Hoeveel elementen?” sta je in het begin met de mond vol tanden. Na vrij veel werk lukt het een klasse van standaardverzamelingen af te zonderen waarmee andere verzamelingen gemeten kunnen worden en zo een `aantal elementen’ opgeplakt kunnen krijgen. Dat wil zeggen: dit werkt voor eindige verzamelingen, waarbij `eindig’ zo wordt gedefinieerd dat `het’ ook inderdaad werkt.
Hoeveel?
Hoe zit het met willekeurige verzamelingen? Georg Cantor dacht dat er zoiets als `het aantal elementen’ moest zijn; hij had zelfs een definitie:
,Mächtigkeit` oder ,Cardinalzahl` von M nennen wir den Allgemeinbegriff, welcher mit Hülfe unseres activen Denkvermögens dadurch aus der Menge M hervorgeht, dass von der Beschaffenheit ihrer verschiedenen Elemente m und von der Ordnung ihres Gegebenseins abstrahirt wird.
Uit die definitie halen we de volgende eisen waar dat Kardinaalgetal C(M) aan zou moeten voldoen:
- M en C(M) hebben even veel elementen (als bij de zakjes snoep), in vaktaal: er is een bijectie tussen M en C(M) — C(M) is dus ook een verzameling
- als er tussen M en N een bijectie bestaan dan C(M)=C(N)
Als er dus zo’n functie is dan kunnen we C(M) `het aantal elementen’ van M noemen.
En, helaas, zo’n functie kun je niet definiëren. Het bewijs van die ondefinieerbaarheid hoop ik maandag 16 december tijdens het laatste college van de Mastermath-cursus Set Theory af te ronden.
Wat betekent dit? Dat verzamelingen geen `intrinsiek’ aantal elementen hebben. Je kunt niet meer doen dan zelf een hoeveelheid standaardverzamelingen af te spreken waarmee je op zinvolle wijze betekenis aan `het aantal elementen’ kunt geven. Getallen zijn geen natuurverschijnselen maar mensenwerk.
Dit gebeurde vaker
De vraag wie van twee mensen langer of korter is is zo beantwoord: hou ze tegen elkaar aan en je ziet het. Om de vraag “Hoe lang zijn die twee mensen?” te beantwoorden zijn in de loop der tijd veel systemen bedacht, sommigen wat logischer dan de andere. Ons metrieke stelsel is overgebleven, ongetwijfeld door de voor de hand liggende definitie van de meter: neem de halve meridiaan van de noordpool door Parijs naar de evenaar en hak die in 10.000.000 even grote stukjes; elk stukje is, per definitie, één meter lang.
Oh, en `teyan-a-bub’? Dat gebruik je bij het tellen van schapen in Weardale.
Boeken, getallen, stellingen
Vorige week ontspon zich een kleine discussie op Twitter over boeken en getallen; Marc van Oostendorp schreef Neerlandistiek.nl over een artikel van Paul Postal waarin de laatste over de aard, de ontologie, van boeken schrijft.
Boeken zijn als getallen. https://t.co/UPA1zENKqx
— Marc van Oostendorp (@fonolog) October 15, 2019
Ietwat kort door de bocht is de these van Postal dat een boek (hij gebruikte Pride and Prejudice als voorbeeld, Marc nam De Kleine Johannes als voorbeeld) als abstract object altijd al bestaan heeft, het is namelijk een rij symbolen (letters, spaties, interpunctie, …) en iemand heeft die rij een keer voor het eerst opgeschreven. Net als het getal gerepresenteerd door 7.987.923.892.274 (gezien de ene hit bij Google waarschijnlijk door Marc als eerste opgeschreven).
Voor het geval de ingebedde tweet hierboven niet goed werkt is hier een korte samenvatting van de discussie.
Mogelijke tegenwerping (Ionica Smeets): elk natuurlijk getal heeft een natuurlijke opvolger, hoe zit dat met boeken? Lijken boeken en stellingen niet meer op elkaar?
Antwoord (Marc): orden ze alfabetisch.
Ander argument (ik): dat werkt niet helemaal, als je alfabetisch wilt werken is Kleene-Brouwerorde beter, maar dan staan tussen elk tweetal boeken weer oneindig veel boeken (ik zag elke rij symbolen als een potentieel boek). Dit geldt overigens ook voor de normale Lexicografische orde van eindige rijen symbolen.
Antwoord (Marc): een boek van vijf miljard pagina’s is lang genoeg. Zou het verschil dan niet zijn dat er maar eindig veel boeken (kunnen) zijn?
Het laatste argument schuurt dan weer met de inhoud van het artikel van Postal (pagina 12): die laat willekeurig lange zinnen toe en concludeert dan dat er niet alleen oneindig veel boeken zijn maar zelfs overaftelbaar veel. Sterker nog: de boeken in een gegeven taal vormen niet eens een verzameling (volgens mij is dat laatste lariekoek maar daar hebben we het later nog wel eens over).
Is er wel verschil?
Je kunt op diverse niveau’s naar deze vraag kijken.
Representaties: rijen symbolen
Als het om opgeschreven verhalen en opgeschreven getallen gaat dan is er inderdaad geen echt verschil: beide bestaan uit rijen symbolen die hun betekenis prijsgeven als je volgens bepaalde regels (in dit geval op school aangeleerd) decodeert.
Bestonden die rijen symbolen ook al voor ze werden opgeschreven? En zo ja, hoe lang al?
Dat is een lastige vraag en waarschijnlijk voer voor lange filosofische discussies. Mijn mening: eigenlijk wel. In ieder geval sinds halverwege de negentiende eeuw (dat maakt het voor Pride and Prejudice wat onzeker): toen begon men namelijk functies als objecten te beschouwen en niet als `formules’ of `regels’. En Cantor nam, gegeven twee verzamelingen X en Y, de verzameling van alle functies van X naar Y ter hand om machtsverheffen van kardinaalgetallen te definiëren.
Als we dus voor een groot genoeg natuurlijk getal N alle functies nemen van {1,2,…,N} naar ons alfabet, aangevuld met spaties en interpunctiesymbolen, dan zit daar het verhaal van De Kleine Johannes (1884) dus ook in. In de tijd van Pride and Prejudice was de wiskunde nog niet zo ver en ik laat het aan de meer filosofisch ingestelden onder ons om te overdenken of dat boek er (ver) voor 1811 ook al was.
Het boek zelf; het getal zelf
Tot nu toe hebben we boek en getal vereenzelvigd met hun representaties. Bij een boek is dat bijna noodzakelijk. We kunnen het boek anders representeren, denk aan een lange rij nullen en enen in een e-reader, maar we hebben bij het lezen toch de oorspronkelijke rij symbolen nodig (tenzij iemand zich heeft aangeleerd de binaire code uit het hoofd te vertalen maar dat lijkt me vergezocht).
Bij een getal is dat niet zo. Neem het getal gegeven in decimale representatie als 1729 (decimale representatie) of als 6C1 (hexadecimaal) of als 11011000001 (binair). Deze representeren alledrie exact dezelfde hoeveelheid stippen, of hoop kogeltjes. En die hoop kogeltjes is de kleinste die op twee verschillende manieren in drie hoopjes verdeeld kan worden die dan elk als kubus gestapeld kunnen worden.
En Stellingen?
Ik was het in eerste instantie met Ionica eens maar nu twijfel ik. Ik vind achteraf dat stellingen dichter bij getallen liggen dan ik dacht. Een stelling heeft vele representaties maar de uiteindelijke betekenis is altijd dezelfde, net als elke representatie van een getal tot dezelfde hoeveelheid stippen, strepen, dropjes zal leiden.
Er is meer
In de tweets hadden we het ook over de mogelijkheid boeken en getallen te ordenen en het al dan niet bestaan van getallen.
Daar zal ik het in een latere post een keer over hebben.
Upgoer Five
Today I was reminded of the Upgoer Five Editor, which was inspired by this XKCD cartoon (an explanation of the workings of the Saturn V rocket in very simple words).
I knew I had tried it once and thanks to twitter I could find my `explanation’ of bijections and a `definition’ of infinity again. This is just a short post so that I have an obvious place to look for the link to that short piece, when I need it.
Also, it will be fun to do this in Norwegian.
Het Probleem uit Katowice
De klimaatttop in Katowice verliep/verloopt moeizaam. Maar het klimaat is niet het enige probleem dat aan Katowice verbonden is.
Het probleem uit Katowice gaat over iets totaal anders. Eén manier om het in te leiden is als volgt. Een eenvoudige opgave: stel dat twee verzamelingen evenveel punten hebben, bewijs dat ze evenveel deelverzamelingen hebben.
Dat klinkt voor de hand liggend en het bewijs is, zeker voor een eerstejaarsstudent, niet moeilijk. De juiste wiskundige formulering van `X en Y hebben evenveel elementen’ is er bestaat een bijectie (ook wel een-een-correspondentie genoemd) f:X→Y tusen de twee verzamelingen. Uit die bijectie maak je met gemak een bijectie F tussen de families deelverzamelingen: F(A)=f[A].
Het omgekeerde probleem zou zijn: stel dat twee verzamelingen evenveel deelverzamelingen hebben, bewijs dat ze evenveel punten hebben.
Dat is een stuk lastiger op te lossen; het lukt nog wel voor eindige verzamelingen want een verzameling met n punten heeft 2n deelverzamelingen en als 2m=2n dan volgt m=n. Echter, dat gebruikt extra informatie, meer dan alleen het bestaan van de bijectie F tussen de families deelverzamelingen. En, geloof het of niet: met alleen de informatie dat zo’n F bestaat is de opgave niet te maken. Dat volgt uit het werk dat Paul Cohen heeft gedaan bij zijn deel van de oplossing van Cantor’s Continuumhypothese: daarbij creërde hij een situatie met twee oneindige verzamelingen met evenveel deelverzamelingen maar niet met evenveel punten.
De som wordt maakbaar als we aannemen dat de bijectie wat meer structuur heeft; als je bijvoorbeeld eist dat F en zijn inverse de deelverzamelingrelatie bewaren, dat wil zeggen A⊂B dan en slechts dan als F(A)⊂F(B), dan kun je wel een bijectie tussen de verzamelingen X en Y maken: F moet namelijk de éeacute;npuntsverzamelingen op elkaar afbeelden en dat geeft automatisch de gewenste bijectie.
In de wiskunde is het soms zo dat we `kleine’ verzamelingen verwaarlozen; zo kunnen we afspreken dat we verzamelingen die maar een eindig aantal punten verschillen als gelijk beschouwen. Dat nu leidt ons tot Het Probleem van Katowice: als je weet dat er afbeelding is die bijectief is en ⊂ respecteert, waarbij eindige verschillen er niet toe doen, kun je dan een bijectie tussen de gegeven verzamelingen maken?
Dat probleem is een stuk moeilijker dan de andere maar het is opgelost, bijna: het antwoord is bijna altijd ja, er zijn twee oneindige verzamelingen, met verschillende aantallen elementen, waarvoor we nog niet hebben kunnen bewijzen dat zo’n bijna-bijectie niet bestaat.
Voor wie meer wil weten: hier is een overzicht van het probleem. Met een waarschuwing: zonder een behoorlijke dosis wiskundige basiskennis is het artikel lastig te lezen.
En waarom is dit Het probleem uit Katowice? Het werd opgeworpen door een student aan de Silezische Universiteit in Katowice en omdat het overgebleven geval zo weerbarstig is gebleken heeft het probleem onder wiskundigen deze naam gekregen.
Fruitmanden samenstellen
Op Facebook stond in de groep Wiskundelessen de volgende vraag (verkort weergegeven): “Hoeveel fruitmanden met zes stuks fruit kun je samenstellen uit vier kiwis, vijf bananen, zes peren, en zeven appels?” De vraagsteller wist dat het antwoord 79 moest zijn maar zag geen manier om daar aan te komen.
Een reageerder vond 79 wel erg weinig want het aantal manieren om 6 dingen uit 22 te kiezen, zonder op de volgorde te letten, is gelijk aan de binomiaalcoëfficiënt 22 boven 6 en die is gelijk aan 74613.
Dat antwoord zou kloppen als de vruchten er wel erg verschillend uit zouden zien. De vraagstelling vermeldt dat niet en het antwoord 79 suggereert dat de vruchten van dezelfde soort ononderscheidbaar zijn.
Hoe pak je zoiets aan? Elke fruitmand is eigenlijk een woord van zes letters, gekozen uit {k,b,p,a}, en gesorteerd: eerst de k’s, dan de b’s, de p’s, en aan het eind de a’s . Bijvoorbeeld kkbbpa, aaaaaa, ppppp, … Die woorden kun je lezen als producten: k2b2pa, a6, p6, … Het komt er dus op neer al dat soort producten te tellen. Hoe doe je dat systematisch, zonder een product te missen?
Dat gaat het best met wat eenvoudige algebra, werk het volgende product uit:
(1+k+k2+k3+k4)(1+b+b2+b3+b4+b5)(1+p+p2+p3+p4+p5+p6)(1+a+a2+a3+a4+a5+a6+a7)
Je krijgt dan alle mogelijke gesorteerde woorden met ten hoogste vier k’s, vijf b’s, zes p’s en zeven a’s.
Nu nog even de woorden van zes letters opzij zetten en tellen: klaar.
Dat kan nog iets sneller: maak van elke letter een x. Elk woord van zes letters wordt dan x6 en dat maakt het uitwerken van het product wat makkelijker.
(1+x+x2+x3+x4)(1+x+x2+x3+x4+x5)(1+x+x2+x3+x4+x5+x6)(1+x+x2+x3+x4+x5+x6+x7)
Met (be)hulp van Maple is het resultaat snel gevonden:
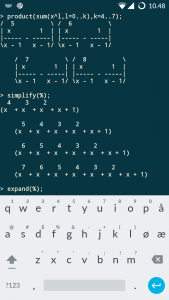

Inderdaad: 79 fruitmanden met zes vruchten. We kunnen nu ook aflezen hoeveel fruitmanden met andere aantallen vruchten gemaakt kunnen worden.
In het februarinummer uit 2016 van Pythagoras staat nog meer over deze manier van combinaties tellen.
Misplacing ones excrement
In the somewhat more colourful language of this site: The Internet is losing its shit over this second grade math problem.
What is the problem?
“There are 49 dogs signed up to compete in the dog show. There are 36 more small dogs than large dogs signed up to compete. How many small dogs are signed up to compete?”
The answers that are discussed on the site are
- 36, with an argument not worthy of the name: 49-36=13, so 13 large dogs, so the answer is 36
- 42.5, because 49-36=13, 13/2=6.5 and 36+6.5=42.5
- 36 once more, but with the added information that 36-13=23, that’s 23 more small dogs
Answers 1 and 3 suffer from something that I observe with many first-year students: I ask something, in a Calculus class it is quite often a primitive function, and many suggestions come flying in, with the expectation that I will deem one of them correct. My reaction then is: you could have checked your answer yourself, in the case of the primitive by differentiation. That is why I asked that question in the first place: to show that they can verify many of their solutions by just substituting back into whatever it was they were solving.
You can verify whether 36 is correct: 36 small dogs is 23 more than 13 large dogs and 23 is definitely not equal to 36. So, no, 36 is not the correct answer.
The second answer — “That’s how I did it in my head.” — is correct, albeit unfortunate for one dog. It is also how I would (try to) explain it to a second-grader.
There are 36 more small dogs than large dogs, so we can set 36 small dogs aside and then look at the remaining dogs. If we want to keep the difference equal to 36 then we must be able to take away two dogs at a time (small and large) from those remaining until we have a group of small and a group of large dogs left. Most likely the second-grader will tell you that that is not going to happen with an odd number of dogs. The conclusion of course is that this is an ill-posed problem.
You can solve this problem — or rather, show it’s unsolvability — in other ways.
The sum of the two numbers in question is odd, that means that they have different parity, i.e., one is odd the and other is even, but then their difference is odd as well and it can’t be 36.
Or you can introduce letters, S and L, and express the demands as equations: S+L=49 and S-L=36. Solving these will lead to the solution done in the head: 2S=85, hence S=42.5 and L=6.5.
I hope that the teacher will admit that there was an error in the problem and that they will turn this into a valuable lesson: you can often check whether your answer is correct or makes sense.
On this day in 1873, II
A little over a week ago I wrote about a letter from Cantor to Dedekind that contained an auspicious question, namely whether the sets of natural and (positive) real numbers could be put into one-to-one correspondence with each other.
On 7 December 1873 Cantor wrote Dedekind with the answer to his question; the answer was (and still is) “no”. The letter contains a proof of the impossibility of a one-to-one correspondence between the two sets.
This was the first time that something like this was done: attempt to compare two infinite entities by pairing off the elements of the sets such that every element of the first was paired with exactly one from the second and vice versa.
Cantor went on to study this idea in depth and he showed how to give a precise meaning to the idea that one set has (strictly) more (or fewer) elements than another set.
To get back to the original question: it is clear that there are at least as many real numbers as there are natural numbers as the latter set is a subset of the former. Cantor’s proof showed that there are strictly more real numbers than there are natural numbers.
There is a difference between this situation and the one mentioned in Cantor’s letter of 29 November, 1873: he mentioned that the natural numbers also form a subset of the positive rational numbers (all fractions of the form p/q with natural numbers p and q). Thus, it seems that there are more such rational numbers than that there are natural numbers. But, we can pair off the members of both sets in such a way that to one member of one set corresponds exactly one member of the other set.
To see this divide the fractions into groups: put fraction p/q into group n if p+q=n. Now observe that group n contains exactly n-1 fractions: 1/(n-1), 2/(n-2), …, (n-1)/1. This makes it easy to arrange the fractions in a nice simple sequence: first group 2, then group 3, then group 4, and so on and inside each group arrange the fractions according to their numerators, as we did above in group n.
The resulting sequence looks like this: 1/1, 1/2, 2/1, 1/3, 2/2, 3/1, 1/4, 2/3, 3/2, 4/1, … and this makes it easy to pair off the natural numbers and the positive fractions as desired.
Exercise Try to devise a formula for the number that goes with the fraction p/q, or, conversely, concoct a formula that tells us what the nth fraction is.
Exercise What would you do if you had to pair off the natural numbers and the positive rational numbers (one rational number corresponds to many fractions).
Here you can read Cantor’s letter in German. It is a scan from Briefwechsel Cantor-Dedekind. And here you can read my translation into English.
On this day in 1873
On this day, 29 November, in 1873 Georg Cantor wrote a letter to Richard Dedekind. It contained a question that inaugurated a new mathematical discipline: Set Theory.
Cantor writes:
Allow me to put a question before you that is of some theoretical interest to me, but which I have not been able to answer; maybe you can, and would you be so kind as to write me about this, it concerns the following.
One takes the aggregate of a positive whole numbers n and denotes this by (n); furthermore one considers the aggregate of all positive real numbers x and denotes this by (x); then the question is simply that whether (n) and (x) can be put into some correspondence in such a way that every individual from one aggregate belongs to just one of the other and conversely?
In modern terms: is there a bijection between the set of natural numbers and the set of positive real numbers?
Cantor goes on to say that a simple `no’ “because (n) is discrete and (x) forms a continuum” does not suffice because the same could be said of (n) versus the aggregate of positive rational numbers yet one can create a correspondence as desired between these two entities.
The full letter can be read here in German. It is a scan from Briefwechsel Cantor-Dedekind.
The answer to the question? Watch this space.
Het Sinterklaasprobleem
Het probleem van vandaag is niet dat van de kleur van de knechten van de Goedheiligman maar dat van het trekken van de lootjes. Wat is de kans dat dat in één keer goed gaat? Kun je het in één keer goed laten gaan?
De kans dat het goed gaat
Als je de namen van alle deelnemers op een papiertje schrijft en daarna iedereen een papiertje uit de hoed (o.i.d.) laat trekken wat is dan de kans dat niemand zichzelf trekt?
Om die kans te kunnen bepalen moet je twee dingen tellen: het totaal aantal manieren waarop de papiertjes uit de hoed getrokken kunnen worden èn het aantal gunstige mogelijkheden. Het laatste aantal gedeeld door het eerste geeft dan de gewenste kans.
Als je dit wiskundig aan wil pakken maak je de situatie zo eenvoudig mogelijk: zet de mensen op een rij, en nummer ze: 1, 2, …, n. Na de trekking zet je persoon i op de plaats van degene die haar getrokken heeft. Op die manier komt een trekking overeen met het op één of andere volgorde zetten van de getallen 1, 2, …, n. Een gunstige trekking is er één waarbij elk getal van zijn (natuurlijke) plaats gehaald wordt.
Je kunt voor kleine n de tellingen met de hand uitvoeren maar het wordt al gauw een beetje onoverzichtelijk: de gevallen n=1 en n=2 zijn een beetje triest, die slaan we maar over. Bij n=3 kunnen we zes trekkingen uitvoeren (schrijf de volgordes maar eens op) en daarvan zijn er twee gunstig: (2,3,1) en (3,1,2). De kans dat het goed gaat is dus 1/3.
Bij een groep van vier mensen zijn er 24 mogelijk trekkingen: de eerste kan vier papiertjes trekken, de tweede drie, de derde twee en de laatste één. Dat levert 4×3×2×1=24 mogelijke volgordes. Het aantal gunstige mogelijkheden is wat lastiger te tellen: je kunt 1 en 2 omwisselen en ook 3 en 4, of 1 en 3 en ook 2 en 4, of 1 en 4 en ook 2 en 3. Dat geeft drie mogelijkheden. Je kunt de getallen ook doorschuiven: zet de mensen in een kring en laat iedereen een positie (naar links) opschuiven; we zetten 1 telkens op dezelfde vaste plek en zetten de andere drie willekeurig neer en dat levert nog zes mogelijkheden. In totaal 9 gunstige rangschikkingen met kans 9/24, ofwel 3/8.
Wie wil puzzelen kan proberen het aantal gunstige rangschikkingen uit de in totaal 5×4×3×2×1=120 manieren om vijf mensen te plaatsen te tellen maar dat wordt al behoorlijk bewerkelijk.
Inclusie-Exclusie
Er is een manier om de telling van het aantal gunstige manieren systematisch te tellen en die manier is ook op veel andere problemen toepasbaar. Het blijkt makkelijker het aantal ongewenste trekkingen te tellen.
Neem een getal n en bekijk de verzameling {1,2,…,n}. Die verzameling kan op n×(n-1)×…×1 manieren gerangschikt worden (het argument hierboven voor n=4 blijft van toepassing). Dat getal noteren we met n! (spreek uit: n-faculteit).
Voor iedere i noteren we de verzameling rangschikkingen die i op haar plaats laten met Di. We willen dus tellen hoeveel elementen er in de vereniging D1∪D2∪…∪Dn zitten.
Voor het gemak voeren we nog de notatie |X| voor het aantal elementen van de verzameling X in.
Teken een plaatje met twee verzamelingen, zeg X en Y, en ga na dat we |X∪Y| als volgt uit kunnen drukken:
|X∪Y|=|X|+|Y|-|X∩Y|
immers: in de som |X|+|Y| tellen we de punten in X∩Y dubbel en daarom moeten we |X∩Y| aftrekken.
Teken een plaatje met drie verzamelingen, X, Y en Z, (met alle mogelijke doorsneden er in) en ga na dat
|X∪Y∪Y∪Z|=|X|+|Y|+|Z|-(|X∩Y|+|X∩Z|+|Y∩Z|)+|X∩Y∩Z|
immers: in |X|+|Y|+|Z| tellen we |X∩Y|+|X∩Z|+|Y∩Z| dubbel, dus dat trekken we af; maar nu zijn de punten in X∩Y∩Z drie keer meegeteld en drie keer afgetrokken, daarom tellen we |X∩Y∩Z| weer op
Als we dit toepassen op het geval n=3 dan krijgen we
|D1|+|D2|+|D3|-(|D1∩D2|+|D1∩D3|+|D2∩D3|)+|D1∩D2∩D3|
als het aantal ongewenste rangschikkingen; omdat |Di|=2 voor elke i, en omdat |Di∩Dj|=1 als i≠j en omdat |D1∩D2∩D3|=1 vinden we 2+2+2-(1+1+1)+1=4 rangschikkingen waarbij ten minste één punt op zijn plaats blijft. We krijgen dus ons eerder gevonden aantal goede rangschikkingen terug.
In het algemene geval gebeurt hetzelfde: eerst de individuele aantallen optellen, dan twee-bij-twee doorsneden aftrekken, drie-bij-drie doorsneden optellen, vier-bij-vier aftrekken …. Dit heet het Principe van Inclusie-Exclusie.
Er zit veel regelmaat in onze aantallen:
- |Di|=(n-1)! (de andere punten mogen willekeurig gerangschikt worden
- |Di∩Dj|=(n-2)! (de andere punten mogen willekeurig gerangschikt worden
- elke k-bij-k doorsnede heeft (n-k)! elementen
Het aantal k-bij-k doorsneden is gelijk aan n!/(k!×(n-k)!) en dat maakt onze berekening heel overzichtelijk: er zijn
![]()
slechte rangschikkingen en dus
![]()
goede rangschikkingen. Als we dat aantal door n! delen komen we uit op een succeskans van
![]()
bij het lootjes trekken met n personen.
Omdat de termen in de som in absolute waarde steeds kleiner worden en beurtelings positief en negatief zijn volgt dat die kans altijd tussen 1/3 en 3/8 zal liggen.
Altijd succes?
Voor wie wil weten hoe je in één keer een goede trekking kunt verrichten: lees deze column van de Wiskundemeisjes uit 2009.
De methode komt er op neer dat je de deelnemers in een kring zet en hun naambriefjes aan de persoon links laat geven (met een truc om het geheim te houden natuurlijk).
Voor wie van puzzelen houdt: vlooi maar eens uit dat de kans dat er bij willekeurig trekken een permutatie als in die column uit komt gelijk is aan 1/n.

Recent Comments