Raaklijnen aan de aarde, I
Zo af en toe kom ik een vraag tegen die opgelost kan worden door naar een raaklijn aan het aardoppervlak te kijken.
Op de website van De Ingenieur verscheen in januari een stuk over een project van de kunstenaar
John Körmeling: het aanleggen van een echt rechte weg. De bedoeling is dat de weg recht is in de zin van `een rechte lijn’: het wegoppervlak ligt dus in een raakvlak aan het aardoppervlak.
De weg van Körmeling (eigenlijk een schelpenpad) wordt zes kilometer lang, drie kilometer naar beide kanten vanuit het raakpunt. In het stuk wordt verteld dat de weg aan de uiteinden zo’n 70 centimeter boven het aardoppervlak komt te liggen. Ik kreeg van een lezer van Pythagoras de vraag of dat wel klopt; het leek wat weinig.
Op de wisfaq werd bijna hetzelfde gevraagd maar over iets grotere afstand: als ik van Zandvoort naar Scheveningen zou lopen over een rechte weg als die van Körmeling hoe hoog boven Scheveningen komt ik dan uit?
De vragen zijn bijna maar niet helemaal hetzelfde: bij de weg van Körmeling weten we hoe lang de rechte lijn zelf is, en bij de tweede vraag weten we de afstand langs het aardoppervlak. Dat heeft gevolgen voor de vorm van de oplossingen, zoals we zo dadelijk zullen zien.
Eerst een plaatje voor de rechte weg
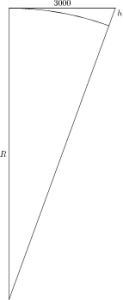
Hier is R de straal van de aarde en h de hoogte van het uiteinde van de weg boven het aardoppervlak. De stelling van Pythagoras brengt hier uitkomst: de onbekende h moet voldoen aan (R+h)2=R2+30002. Als we dit naar h oplossen komt er
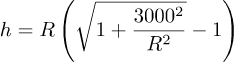
We zullen h zometeen uitrekenen maar eerst kijken we naar de wandeling van Zandvoort naar Scheveningen.
Eerst weer een plaatje
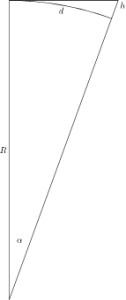
Nu weten we de lengte van het boogje, hier aangegeven met d. Voor de oplossing van het probleem is de hoek α ook van belang. Er geldt namelijk
![]()
en hieruit is h op te lossen:
![]()
De formules zien er inderdaad anders uit en beide kunnen makkelijk met (be)hulp van een rekenmachientje uitgewerkt worden. Voor R, de straal van de aarde, vullen we 40000000/(2π) m in (de omtrek van de aarde is namelijk per definitie 40000 km). Voor de hoogte van het uiteinde van de weg krijgen we iets meer dan 70 centimeter: 70,66479472 cm.
Mijn antwoord aan die lezer was dus: “Ja, het klopt.”
Margriet van der Heiden heeft er in haar rubriek Vormen en Getallen ook over geschreven:
NRC: 27-01-2017 (gedrukte versie: 28-01-2017).
Voor de wandeling van Zandvoort naar Scheveningen geldt dat de hoek α gelijk is aan d/R (we werken in radialen). Google maps geeft aan dat de wandeling van station Zandvoort naar de Pier van Scheveningen 38 km is, we nemen dus d=38000 m. Mijn rekenmachientje geeft aan dat we zo’n 113 m boven Scheveningen eindigen (113,4132864 volgens mijn rekenmachientje).
Morgen zullen we zien dat er minder verschil tussen de twee vragen zit als misschien lijkt, maar voor nu een paar opgaven.
Opgave 1: Als John Körmeling:de weg in zou (laten) graven hoe diep zou de weg dan in het midden liggen?
Opgave 2: Aangenomen dat het pad een meter breed wordt: hoeveel kubieke meter schelpen moet er aangevoerd worden?
Hoeveel grond zou weggegraven moeten worden bij de ingraafmethode?
Opgave 3: Bij de wandeling van Zandvoort naar Scheveningen is de afstand afgerond tot 38000 m.
Probeer andere waarden van d om te zien wat de invloed van die afronding op de hoogte is.
Vergroot/verklein d in stappen van 100 m bijvoorbeeld.





Recent Comments